Afiliacja: University of Education Weingarten (HS), XX Liceum Ogólnokształcące w Krakowie (BP)
Najpewniej każdy Czytelnik Delty wie, co to jest sześcian – i że co do zasady (fachowo: co do podobieństwa) jest tylko jeden taki w geometrycznym świecie. W niniejszym artykule odpowiemy na pytanie, ile jest sześciościanów wypukłych, czyli brył, od których wymagamy jedynie wypukłości i posiadania sześciu ścian. Nie będziemy przy tym rozróżniać wielościanów różniących się jedynie ułożeniem wierzchołków w przestrzeni – na przykład sześcian oraz ścięty ostrosłup czworokątny (patrz margines) liczymy jako ten sam sześciościan.
Rozpocznijmy od przypomnienia wzoru Eulera: jeśli pewien wypukły wielościan ma \(s\) ścian, \(k\) krawędzi oraz \(w\) wierzchołków, to zachodzi: \[\label{eq:euler} s-k+w=2.\] Zauważmy ponadto, że z każdą krawędzią związane są dwa wierzchołki (jej końce) oraz z każdym wierzchołkiem związane są co najmniej trzy krawędzie (te, do których ów wierzchołek należy). Podobnie, z każdą krawędzią związane są dwie ściany, a z każdą ścianą – co najmniej trzy krawędzie. Wynikają stąd nierówności: \[\label{eq:baseineq} 2k\geq 3w\ \ \ \textrm{oraz}\ \ \ 2k\geq 3s.\] Wstawiając w powyższych nierównościach \(k=w+s-2\) (co wynika ze wzoru Eulera), otrzymamy ostatecznie \[\tfrac{1}{2}s+ 2 \leq w \leq 2s -4.\] Przyjmując wyżej \(s=6,\) otrzymujemy, że liczba wierzchołków sześciościanu może wynosić 5, 6, 7 lub 8. Dostajemy w ten sposób cztery kategorie sześciościanów, w ramach których każdy ma taką samą liczbę wierzchołków (więc również krawędzi). Różnice dotyczą konfiguracji ścian bocznych. Mogą być nimi tylko trójkąty, kwadraty i pięciokąty – sześciokąty nie są możliwe, gdyż taka ściana musiałaby mieć dodatkowych sześć sąsiadujących ścian.
Aby dobrze oswoić się ze wzorem Eulera, polecamy poświęcony mu Deltoid z \(\Delta^{3}_{16}\)oraz tekst Polowanie na uroczy wielościan z \(\Delta^3_{16},\) które w podobny sposób wykorzystuje wzór Eulera.
Wyniki naszych wstępnych poszukiwań przedstawia poniższa tabela. Wielkości \(s_3,\) \(s_4\) i \(s_5\) oznaczają odpowiednio liczbę ścian trój-, czworo- i pięciokątnych.
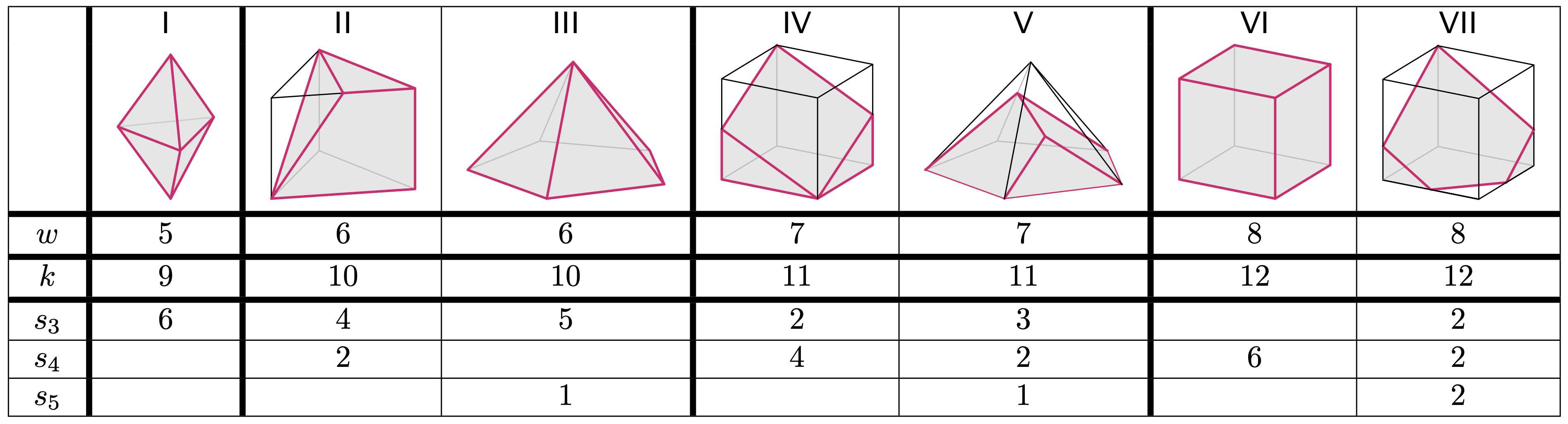
Znaleźliśmy siedem różnych sześciościanów. Skąd jednak wiadomo, że nie ma innych? Łatwo uwierzyć, że z 6 trójkątów można zbudować tylko wielościan typu I, z 5 trójkątów i pięciokąta tylko wielościan typu III, z 6 czworokątów tylko wielościan typu VI, z kolei z dwóch pięciokątów, które muszą mieć wspólną krawędź, tylko typ VII. Badanie wielu przypadków kombinacji ścian dla pozostałych konfiguracji \((w,s_3,s_4,s_5)\) nie jest jednak zbyt obiecujące. W sukurs przyjdą nam pewne dodatkowe narzędzia teoretyczne.
Rozpatrzmy pewien wielościan wypukły \(\mathcal{W}.\) Wybierzmy dowolne punkty na ścianach tego wielościanu i połączmy odcinkami pary punktów leżące na sąsiadujących ścianach. To, co w rezultacie dostaniemy, może nie być wielościanem, gdyż niedoszłe ściany mogą być ,,powyginane”. Okazuje się, że uzyskany szkielet można jednak ,,wyprostować”, otrzymując pełnoprawny wielościan \(\mathcal{W}',\) który nazywamy wielościanem dualnym \(\mathcal{W}.\) Nietrudno przekonać się, że wielościan dualny ma tyle samo krawędzi co oryginalny, zaś liczba jego ścian jest równa liczbie wierzchołków wyjściowego (i vice versa). Ponadto wielościan dualny do dualnego jest (co do struktury) tożsamy z wyjściowym. W szczególności, wielościan dualny jednoznacznie wyznacza swój oryginał.
Wielościany typu I i \(\textsf{II}\) wraz ze swoimi wielościanami dualnymi
Wyobraźmy sobie teraz, że ściany danego wielościanu są przezroczyste, w odróżnieniu od jego krawędzi. Z jednej strony takiego wielościanu przykładamy źródło światła, a z drugiej kartkę. Jeśli odpowiednio przyłożymy źródło światła, cienie krawędzi nie będą się przecinać – uzyskamy w ten sposób diagram Schlegela wielościanu. Jeśli spojrzymy na diagram Schlegela jak na graf, czyli układ punktów (wierzchołków) połączonych kreskami (krawędziami), to będziemy mogli stwierdzić, że jest on grafem planarnym, czyli możliwym do narysowania bez przecinania krawędzi.
Wielościan i jego cień, czyli diagram Schlegela. David Eppstein, CC BY-SA 3.0, via Wikimedia Commons
Diagram Schlegela ma jeszcze jedną własność – jest grafem spójnym, czyli poruszając się po jego krawędziach, można przemieścić się między dowolnymi jego wierzchołkami (bo tak też jest na wielościanie). Dla wielościanów wypukłych pozostaje to prawdą, nawet jeśli pozbędziemy się dowolnych dwóch wierzchołków wraz z wychodzącymi z nich krawędziami (szkic uzasadnienia na marginesie). Można równoważnie powiedzieć, że każde dwa wierzchołki są połączone co najmniej trzema ścieżkami, które – oprócz początku i końca – nie mają punktów wspólnych. Takie grafy nazywamy trójspójnymi.
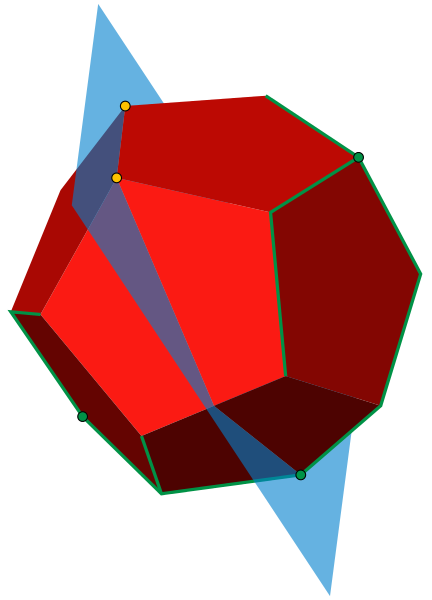
Uzasadnienie 3-spójności diagramu Schlegela w pigułce: wybierzmy dowolne wierzchołki \(w\) i \(v\) wielościanu \(\mathcal{W}.\) Udowodnimy, że dowolne dwa inne wierzchołki można połączyć ścieżką, która nie przechodzi ani przez \(u,\) ani przez \(v.\) Rozważmy płaszczyznę przechodzącą przez \(w,\) \(v\) i jeszcze jeden (dowolny) wierzchołek \(u.\) Rozbija ona \(\mathcal{W}\) na dwie części. Wierzchołki każdej z nich można zwiedzić, startując z \(u\) i poruszając się po krawędziach, które nie mają końca w \(w\) i \(v.\) Ilustracja: David Eppstein, CC BY-SA 4.0, via Wikimedia Commons
Zgodnie z powyższymi obserwacjami diagramy Schlegela wielościanów dualnych do sześciościanów są planarnymi i trójspójnymi grafami o sześciu wierzchołkach. Na szczęście dla nas w publikacji [\(\dagger\)] przedstawiono spis wszystkich 112 spójnych grafów o 6 wierzchołkach, z informacją (między innymi) o ich planarności i stopniu spójności. Ostatecznie zostajemy z siedmioma grafami:

Dowiedliśmy w ten sposób, że istnieje co najwyżej 7 sześciościanów – udało się nam zatem przedstawić wszystkie. Czytelnikowi Podejrzliwemu pozostawiamy sprawdzenie, czy przedstawione wyżej grafy faktycznie są diagramami Schlegela wielościanów dualnych do zaprezentowanych wcześniej sześciościanów. Zaznaczmy przy okazji, że trójspójność i planarność to wystarczające warunki, by dany graf mógł być ,,cieniem” jakiegoś wielościanu. Jest to głębokie twierdzenie udowodnione przez niemieckiego matematyka Ernsta Steinitza (1871–1928).
Na koniec wspomnijmy, że istnieją trzy typy niewypukłych sześciościanów, które można
skonstruować poprzez odpowiednie wycięcie czworościanu z czworościanu.
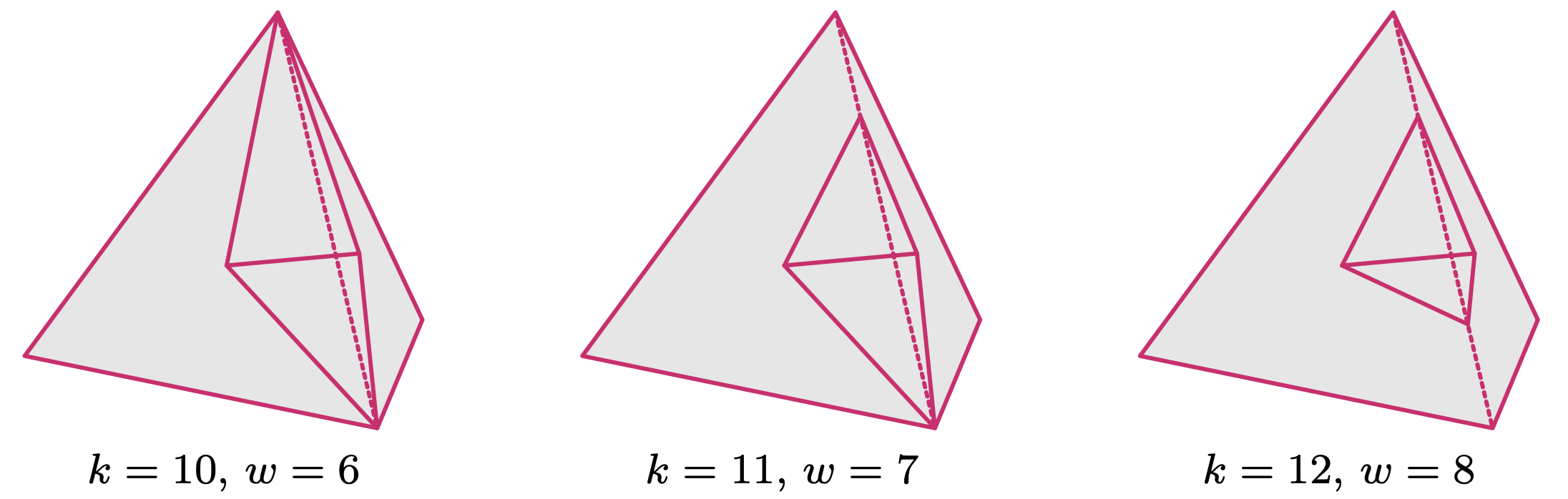
Literatura
[\(\dagger\)] Cvetković Dragoš i Milenko Petrić, ,,A table of connected graphs on six vertices”, Discrete Mathematics 50 (1984): 37–49.
Grafy tych wielościanów niewypukłych, a co za tym idzie także grafów ich wielościanów dualnych, nie są trójspójne. Tych wielościanów nie udałoby się zatem ,,uwypuklić” i są to przykłady istotnie różne od tych zaprezentowanych wcześniej.