Równania różniczkowe jako hieroglify

W tym artykule zamierzamy przybliżyć bogactwo świata równań różniczkowych i związanych z nimi zagadnień w szerokim kontekście – obejmującym matematykę, fizykę i filozofię nauki – na przykładzie równania, które symbolicznie zapisujemy jako $$\mathrm{△}u=f.$$ Za tym napisem kryją się całe misternie skonstruowane światy. Możemy go traktować jako hieroglif, który należy dopiero rozszyfrować, dokładnie tak samo jak to było z hieroglifami egipskimi na kamieniu z Rosetty (rys. 1). Podobnie każdy tekst matematyczny (rys. 2 i 3) musimy najpierw rozszyfrować, a potem zrozumieć na różnych poziomach (o czym pisaliśmy również w ${\mathrm{\Delta }}_{22}^1$).

Pierwsza rzecz to rozszyfrowanie znaczenia znaków $\mathrm{△},$ $u,$ $=$ oraz $f.$ Znak $=$ podpowiada, że napis $\mathrm{△}u=f$ wyraża równanie, a więc język tego napisu jest językiem matematyki, ale nie wiemy, jakie mają znaczenie symbole $u,$ $f$ oraz $\mathrm{△}u.$ Które z tych obiektów oznaczają liczby, funkcje, a może jeszcze coś innego?

Rzeczywiście, interpretacji może być wiele. Skupmy się, zgodnie z porządkiem historycznym, na interpretacji klasycznej, gdzie $u,$ $f$ są funkcjami w przestrzeni euklidesowej jedno-, dwu- lub trójwymiarowej, a $\mathrm{△}$ oznacza operator różniczkowy. W przypadku dwuwymiarowym, czyli na płaszczyźnie, dla funkcji $u$ i $f$ dwóch zmiennych $x_1,x_2,$ napis $\mathrm{△}u=f$ odczytujemy jako $$\begin{array}{}\text{(1)}& \mathrm{△}u(x_1,x_2)=\frac{{\partial }^{2}u(x_1,x_2)}{\partial x_1^2}+\frac{{\partial }^{2}u(x_1,x_2)}{\partial x_2^2}=f(x_1,x_2),\end{array}$$ gdzie $\frac{{\partial }^2}{\partial x_i^2}$ oznacza drugą pochodną cząstkową po $i$-tej współrzędnej. (Pochodne cząstkowe można rozumieć jako ,,zwykłe” pochodne przy ,,zamrożeniu” wartości wszystkich zmiennych poza jedną, po której pochodna cząstkowa jest liczona).

No dobrze, ale o co nam chodzi, gdy piszemy równanie $\text{(1)}$? Równania różniczkowe rozumiemy podobnie jak równania algebraiczne. Na przykład, mając równanie $x^2=a,$ dla danej liczby $a$ możemy zadać pytanie, czy istnieje liczba $x,$ która to równanie spełnia, a jeśli tak – jak możliwie prosto przedstawić zbiór wszystkich takich liczb (tzn. zbiór rozwiązań). Liczba $a$ może nie być sprecyzowana, jednak bywa, że nakładane są na nią pewne dodatkowe warunki (np. że jest liczbą dodatnią). Podobnie rozwiązań możemy chcieć szukać w jakimś określonym zbiorze, np. w zbiorze liczb wymiernych.

W przypadku naszego równania różniczkowego, analogicznie, dla danej ciągłej funkcji $f$ należy znaleźć funkcję $u$ mającą ciągłe pierwsze dwie pochodne i spełniającą równość $\text{(1)}$ w każdym punkcie $(x_1,x_2).$

Podstawowe pytania w obu sytuacjach są te same.

(A) Czy dla wybranych danych ($a$ czy $f,$ odpowiednio) istnieje rozwiązanie ($x$ czy $u,$ odpowiednio) danego równania, a jeśli tak, to ile takich rozwiązań jest?

(B) Jakie są własności rozwiązań?

Wiemy, że w przypadku równania $x^2=a,$ gdy $a$ jest liczbą dodatnią, to istnieją dwa rzeczywiste rozwiązania, symetryczne względem 0. Oznaczamy je jako $\sqrt{a}$ (dodatnie) oraz $-\sqrt{a}.$ Dla $a=0$ mamy jedno rozwiązanie: $x=0,$ a dla $a$ ujemnych nie istnieje liczba rzeczywista $x$ spełniająca równanie $x^2=a.$

Zagadnienie jednowymiarowe. Zilustrujemy nasze pytania dotyczące istnienia i własności rozwiązań równania $\mathrm{△}u=f$ w najprostszym, jednowymiarowym przypadku. Nasze równanie przybiera wtedy postać $$\begin{array}{}\text{(2)}& \frac{d^{2}u(x)}{d{x}^2}=f.\end{array}$$ Weźmy $f=0.$ Jest to bardzo ważny przypadek, nazywany jednorodnym. Jeżeli $$\begin{array}{}\text{(3)}& \frac{d^{2}u(x)}{d{x}^2}=0,\end{array}$$ to nietrudno jest zobaczyć, że rozwiązania istnieją i mają postać $$u(x)=ax+b,$$ gdzie $a$ i $b$ mogą być dowolnymi liczbami rzeczywistymi. Zatem nasze równanie różniczkowe ma nieskończenie wiele rozwiązań, wykresami których są proste. Jest to odpowiedź na pytanie (A) o istnienie i liczbę rozwiązań.

Do ważnych (i oczywistych) własności naszych rozwiązań, mających swoje naturalne (choć nieco mniej oczywiste) uogólnienia także w przypadku dwu- i trójwymiarowym, należą:

1. Dla dowolnego odcinka $(A,B)$ rozwiązanie równania $\text{(3)}$ przyjmuje swoje ekstrema, czyli wartości najmniejszą i największą, na jego końcach (tzn. na brzegu tego odcinka). Jeśli rozwiązanie nie jest funkcją stałą, to wartości ekstremalne są przyjmowane wyłącznie na krańcach odcinka.

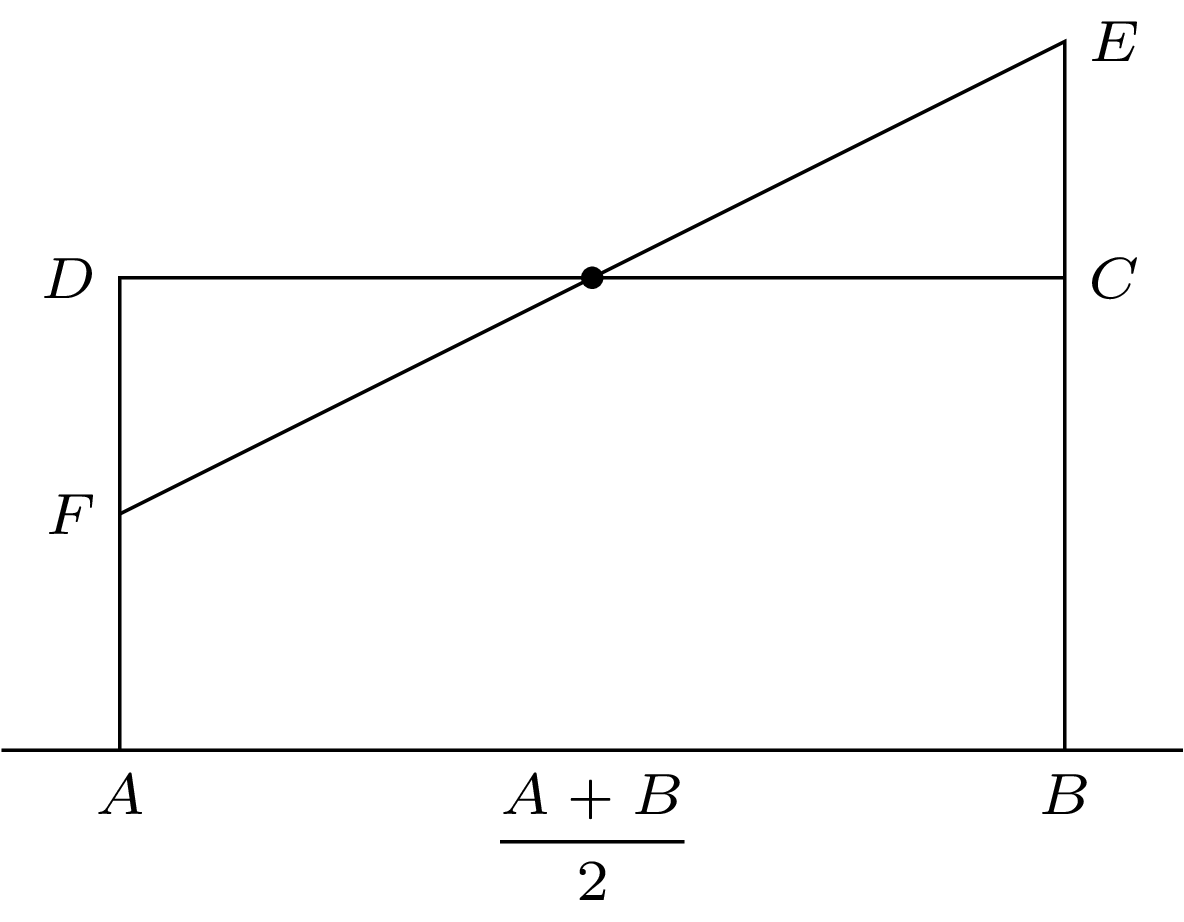
2. Dla dowolnego odcinka $(A,B)$ rozwiązanie równania $\text{(3)}$ w środku tego odcinka przyjmuje wartość równą średniej z wartości przyjmowanych na brzegach odcinka, czyli $u(\frac{A+B}{2})=\frac{u(A)+u(B)}{2}$ (rys. 4).

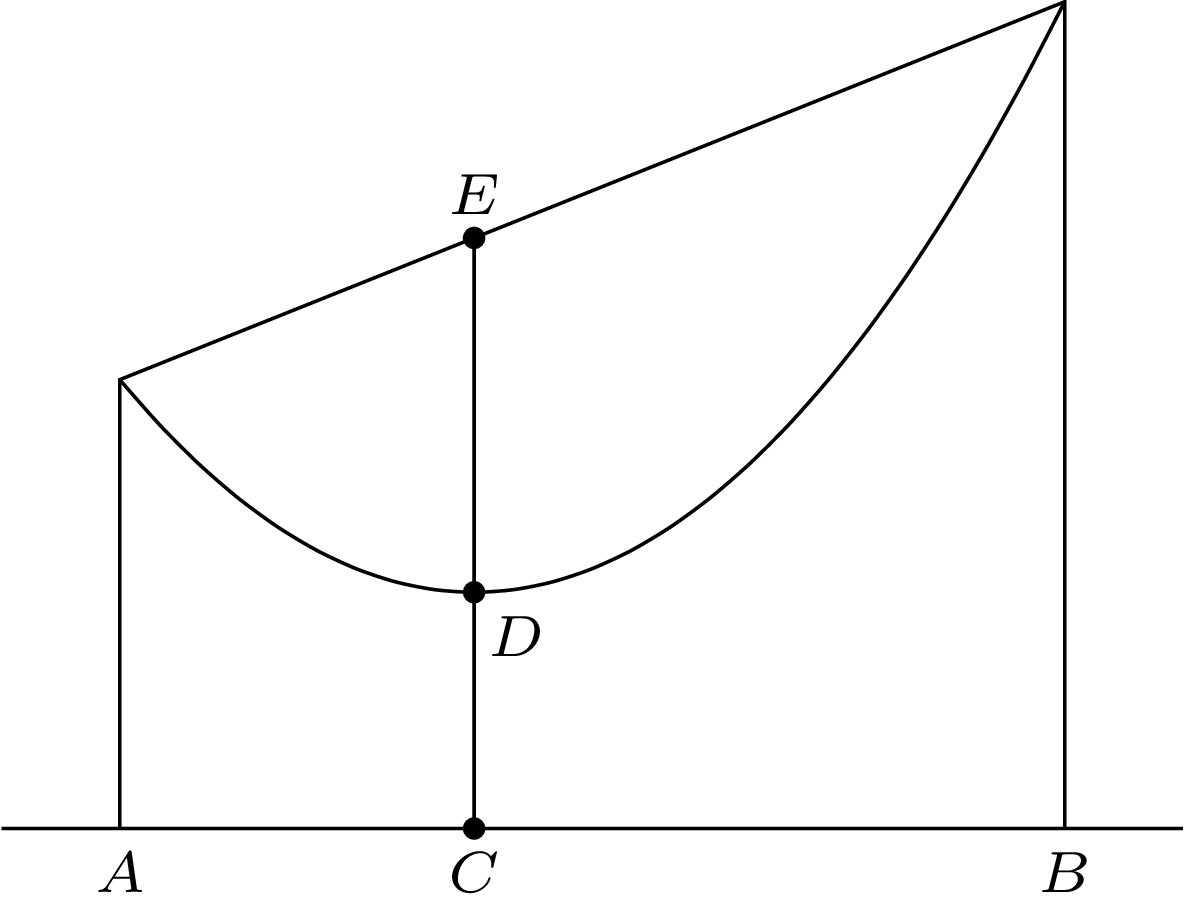
3. Dla dowolnego odcinka $(A,B)$ rozwiązanie równania $\text{(3)}$ w środku tego odcinka przyjmuje wartość średnią na tym odcinku, co znaczy, że pole pod wykresem rozwiązania na odcinku $(A,B)$ jest równe polu prostokąta o podstawie $B-A$ i wysokości $u(\frac{A+B}{2})$ (rys. 5).

Rozważymy teraz prosty przykład równania niejednorodnego, $$\frac{d^{2}u(x)}{d{x}^2}=2\mathrm{l}\mathrm{u}\mathrm{b}{u}^{″}(x)=2.$$ Z powyższego równania widzimy, że druga pochodna funkcji $u$ jest dodatnia, a więc pierwsza pochodna jest funkcją rosnącą, w konsekwencji funkcja $u$ jest ściśle wypukła, czyli na każdym odcinku $(A,B)$ leży poniżej swojej siecznej na tym odcinku, co opisuje warunek $u(\alpha A+(1-\alpha )B)<\alpha u(A)+(1-\alpha )u(B)$ dla każdej liczby $\alpha$ z przedziału $(0,1).$ W naszym przypadku $u(x)=x^2+bx+c$ (rys. 6).

Wymienione powyżej własności II i III mają swoje uogólnienia dla rozważanego równania niejednorodnego. Wyglądają one następująco: $$\begin{array}{}\text{(4)}& \frac{u(p+h)+u(p-h)}{2}=u(p)+\frac{1}{2}{u}^{″}(p)h^2\end{array}$$ oraz $$\begin{array}{}\text{(5)}& \frac{1}{2h}{\int }_{p-h}^{p+h}u(r)dr=u(p)+\frac{1}{6}{u}^{″}(p)h^2\end{array}$$ dla dowolnego ustalonego punktu $p.$ W szczególności, gdy funkcja $u$ spełnia równanie $u^{″}(x)=0,$ otrzymujemy własności II i III, a w ogólniejszym przypadku powyższe wzory mówią nam, że operator $\frac{d^2}{d{x}^2}$ mierzy odchylenie wartości funkcji w danym punkcie $p$ od wartości średnich, zdefiniowanych przez lewe strony równań $\text{(4)}$ i $\text{(5)}$ odpowiednio, na zawierającym go przedziale $(p-h,p+h).$

Jak to wygląda od strony fizyki? Spójrzmy teraz na równania $\text{(2)}$ i $\text{(3)}$ od strony fizyki, a obraz nam się rozjaśni.

Równanie $\text{(3)}$ opisuje następującą sytuację fizyczną. Załóżmy, że mamy pręt (obiekt jednowymiarowy) o długości $B-A,$ na którego końcach $A,$ $B$ utrzymujemy stałą temperaturę $u(A)$ i $u(B).$ Pytamy o temperaturę $u(x)$ w każdym wewnętrznym punkcie pręta. Po bardzo długim czasie od początku eksperymentu rozkład temperatury w pręcie powinien się ustalić do funkcji spełniającej równanie $\text{(3)}$, a więc do funkcji liniowej łączącej punkty $(A,u(A))$ i $(B,u(B)).$

Jeżeli natomiast w punkcie $p$ we wnętrzu obszaru znajduje się źródło ciepła (co odpowiada temu, że $f(p)<0$), to temperatura w punkcie $p$ będzie większa niż średnia temperatura w jego otoczeniu. Taką sytuację opisuje równanie $\text{(2)}$.

W świetle tej interpretacji własności I, II i III oraz wzory $\text{(4)}$, $\text{(5)}$ stają się zrozumiałe.

Zagadnienie brzegowe a zagadnienie początkowe. Poszukiwanie granicznego rozkładu temperatury w pręcie możemy przedstawić w postaci następującego zagadnienia brzegowego: $$\begin{array}{}\text{(6)}& \frac{d^{2}u(x)}{d{x}^2}=f(x),A<x<B,u(A)=u_A,u(B)=u_B.\end{array}$$ Szukamy tu funkcji $u(x)$ określonej na odcinku $[A,B],$ spełniającej równanie różniczkowe wewnątrz tego odcinka i powyższe warunki na jego brzegach, dla ustalonych liczb $u_A$ i $u_B.$

Równanie $\text{(6)}$ jest równaniem należącym do mechaniki klasycznej w przebraniu, ponieważ równanie $$\begin{array}{}\text{(7)}& m\frac{d^{2}x(t)}{d{t}^2}=f(x(t)),A<t<B,x(A)=x_A,x(B)=x_B\end{array}$$ opisuje ruch ciała o masie $m$ w polu sił $f,$ w przedziale czasu $A<t<B,$ z zadanymi położeniami początkowym $x_A$ oraz końcowym $x_B.$

W mechanice klasycznej Newtona równanie $\text{(7)}$ uzupełnione jest zwykle podaniem warunków początkowych postaci $x(A)=x_A,$ $\frac{dx}{dt}(A)=v_A,$ to znaczy podaniem położenia i prędkości ciała w chwili $A.$ Otrzymujemy wtedy zagadnienie początkowe: $$\begin{array}{}\text{(8)}& m\frac{d^{2}x(t)}{d{t}^2}=f(x(t)),A<t<B,x(A)=x_A,\frac{dx}{dt}(A)=v_A.\end{array}$$ Zagadnienie początkowe zgodne jest z zasadą przyczynowości w fizyce, która mówi, że przyczyna zawsze poprzedza skutek. Mając prawo ruchu i warunki początkowe w chwili $A,$ chcemy wyznaczyć trajektorię ruchu $x(t)$ na przedziale $(A,B).$

Warto zauważyć, że równanie Newtona jest odwracalne w czasie, tzn. nie zmienia się, gdy odwrócimy czas, z $t$ na $-t.$ Aby się o tym przekonać, rozważmy razem z problemem $\text{(8)}$ problem $$m\frac{d^2\hat{x}(t)}{d{t}^2}=f(\hat{x}(t)),A<t<B,\hat{x}(A)=x(B),\frac{d\hat{x}}{dt}(A)=-\frac{dx(B)}{dt},$$ którego rozwiązanie $\hat{x}(t)=x(A+B-t)$ jest wyznaczone na przedziale $(A,B).$ Opisuje ono tę samą drogę, tylko w odwrotnym kierunku i z wektorami prędkości przeciwnie skierowanymi.

Tkwi w tym pewien dylemat opisu rzeczywistości, dotyczący fundamentalnych problemów fizyki: strzałki czasu, procesów nieodwracalnych, demona Maxwella i rosnącej entropii. Wiele razy chcielibyśmy odwrócić czas tylko na chwilę, ,,puścić film do tyłu”, aby rozbity wazon w całości wrócił na swoje miejsce… Jest to praktycznie niemożliwe, ale równania Newtona o tym nie mówią.

Sformułowanie wariacyjne i jego interpretacje. Zagadnienie brzegowe $\text{(6)}$ możemy interpretować następująco. Mamy prawo ruchu i zadane dwa punkty $(A,u_A)$ i $(B,u_B)$ w przestrzeni $(x,u).$ Chcemy wyznaczyć trajektorię $u(x)$ spełniającą równanie różniczkowe $\text{(6)}$ i łączącą te punkty, tzn. aby $u(A)=u_A$ i $u(B)=u_B,$ $A\le x\le B$ (rys. 7).

Okazuje się, że rozwiązanie $u$ zagadnienia $\text{(6)}$ minimalizuje wyrażenie $$\begin{array}{r}F(u)={\int }_A^B\frac{1}{2}|\frac{du(x)}{dx}{|}^{2}dx+{\int }_A^{B}f(x)u(x)dx.\end{array}$$ Oznacza to, że dla wszystkich funkcji $v(x)$ spełniających warunki brzegowe $v(A)=u_A,v(B)=u_B$ na końcach przedziału $(A,B)$ $$\begin{array}{r}F(v)\ge F(u),\end{array}$$ gdzie funkcja $u(x)$ jest rozwiązaniem zagadnienia $\text{(6)}$.

Rozważmy szkolne zadanie ruchu w pionie w polu grawitacyjnym Ziemi (np. badamy ruch podrzuconej piłki). Jeśli oś $Ox$ jest skierowana do góry, to funkcję $f$ reprezentuje liczba $-mg,$ gdzie $g$ jest stałą grawitacji.

Z tego, co powiedzieliśmy wyżej, trajektoria ruchu minimalizuje wyrażenie $$\begin{array}{r}F(x)={\int }_A^B\frac{m}{2}|\frac{dx(t)}{dt}{|}^{2}dt-{\int }_A^{B}mgx(t)dt={\int }_A^B\{\frac{m}{2}|\frac{dx(t)}{dt}{|}^2-mgx(t)\}dt,\end{array}$$ gdzie $\frac{m}{2}|\frac{dx(t)}{dt}{|}^2$ jest energią kinetyczną, a $mgx$ energią potencjalną poruszającego się ciała.

Jeśli $g=0,$ to ruch od punktu $x_A$ do punktu $x_B$ odbywa się po prostej łączącej te punkty ze stałą prędkością, co jest zgodne z pierwszym prawem Newtona mówiącym, że każdy obiekt pozostanie w spoczynku lub w ruchu jednostajnym po linii prostej, chyba że zostanie zmuszony do zmiany swojego stanu przez działanie siły zewnętrznej. Ta tendencja do przeciwstawiania się zmianom stanu ruchu nazywana jest bezwładnością, a prawo to jest również nazywane prawem bezwładności.

W świetle powyższego zauważmy, że drugą zasadę ruchu w mechanice Newtona można sformułować jako zasadę najmniejszego działania: średnia energia kinetyczna pomniejszona o średnią energię potencjalną jest możliwie najmniejsza na drodze obiektu biegnącego z jednego punktu do drugiego.

W szczególności pierwsza i druga zasada ruchu wynikają z zasady najmniejszego działania.

Zauważmy coś dziwnego. Zasada najmniejszego działania głosi w szczególności, że wybór punktu początkowego $x(A)=x_A$ i docelowego $x(B)=x_B$ wyznacza drogę ciała w przedziale czasu $(A,B).$ Wydaje się, że jest to sprzeczne z prawem przyczynowości.

Kiedy znajdziemy $x(t)$ rozwiązujące problem $\text{(7)}$, obliczymy wyrażenie $\frac{dx}{dt}(A)=v_A,$ a następnie rozwiążemy problem $\text{(8)}$, to rozwiązanie drugiego problemu będzie pokrywać się z rozwiązaniem pierwszego. Możemy o tym myśleć w następujący sposób: wybór punktu docelowego $x_B$ w chwili $B$ wyznacza właściwą prędkość $v_A$ we wcześniejszej chwili $A.$

Istotnie, tkwi tu pewna tajemnica – w jaki sposób ciało ,,wybiera” rzeczywistą ścieżkę spośród wszystkich możliwości ruchu lub dlaczego rzeczywista historia wymaga minimalnego działania.

Z drugiej strony możemy uznać za rzecz naturalną owo nieprzyczynowe wyjaśnienie praw mechaniki i nazwać je wyjaśnieniem poprzez więzy [Mrówczyński, 1991], [Lange, 2017], [Glick, 2023]. Należy pamiętać, że zasada przyczynowości nie jest jakąś prawdą absolutną, a zaledwie użytecznym paradygmatem, od dawna uważanym za tajemniczy i zagadkowy – samo zdefiniowanie pojęcia ,,przyczyny” sprawia trudności – a obecnie coraz bardziej uwierającym w fizyce.

Problem zasady najmniejszego działania (w fizyce i nie tylko tam) był i wciąż jest dyskutowany przez najwybitniejszych uczonych i filozofów. Matematyk może powiedzieć, że sformułowanie wariacyjne jest tylko jednym z równoważnych sformułowań praw dynamiki, fizyk może bronić zasady najmniejszego działania, np. podając jej wyjaśnienia na gruncie fizyki kwantowej, inni widzą w niej niezbadane jeszcze prawa ekonomii przyrody czy celowości przyrody lub kryjącego się za nią Wielkiego Projektanta.

Artykuł rozpoczęliśmy od przedstawienia prostego hieroglifu $\mathrm{△}u=f$ ukrywającego w sobie równanie różniczkowe. Ledwie tylko wniknąwszy w jego głąb, napotkaliśmy zagadnienia należące do trzech dziedzin: matematyki, fizyki i filozofii nauki. Nasz hieroglif naprowadził nas na pytania dotyczące ich interpretacji i wzajemnych powiązań, inspirując do poszerzenia spojrzenia i dalszych poszukiwań, albowiem: Więcej jest rzeczy na niebie i na ziemi, Horacy, niż te wyobrażalne w twojej filozofii.