Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Ten artykuł jest niezamierzoną trzecią częścią mimowolnej trylogii o punktach kratowych. Jak wiadomo, muszkieterowie, aby dobrze współdziałać, muszą się wzajemnie bacznie i nieustannie obserwować. Żyją oni na kracie całkowitoliczbowej w punktach \((m_1^{(j)},m_2^{(j)})\) dla \(j=1,2,\ldots,k ,\) gdzie \(k\geq 2\) jest liczbą muszkieterów. Muszkieterowie o numerach \(j_1,\) \(j_2\) widzą się wtedy i tylko wtedy, gdy na odcinku między nimi nie ma żadnego punktu kratowego (rys. 1), to znaczy, gdy NWD\((m_1^{(j_2)}-m_1^{(j_1)},m_2^{(j_2)}-m_2^{(j_1)})=1.\) Dla \(k=2\) możemy mówić o muszkieterze i muszkieterce, co czyni całą sytuację dodatkowo romantyczną.
Poprzednie części trylogii to: K. Łyczek, Widoczność w nieskończonym lesie \((\Delta_{20}^4),\) K. Łyczek, M. Skałba, Nigdy Cię nie zobaczę (\(\Delta_{20}^{12}\)).
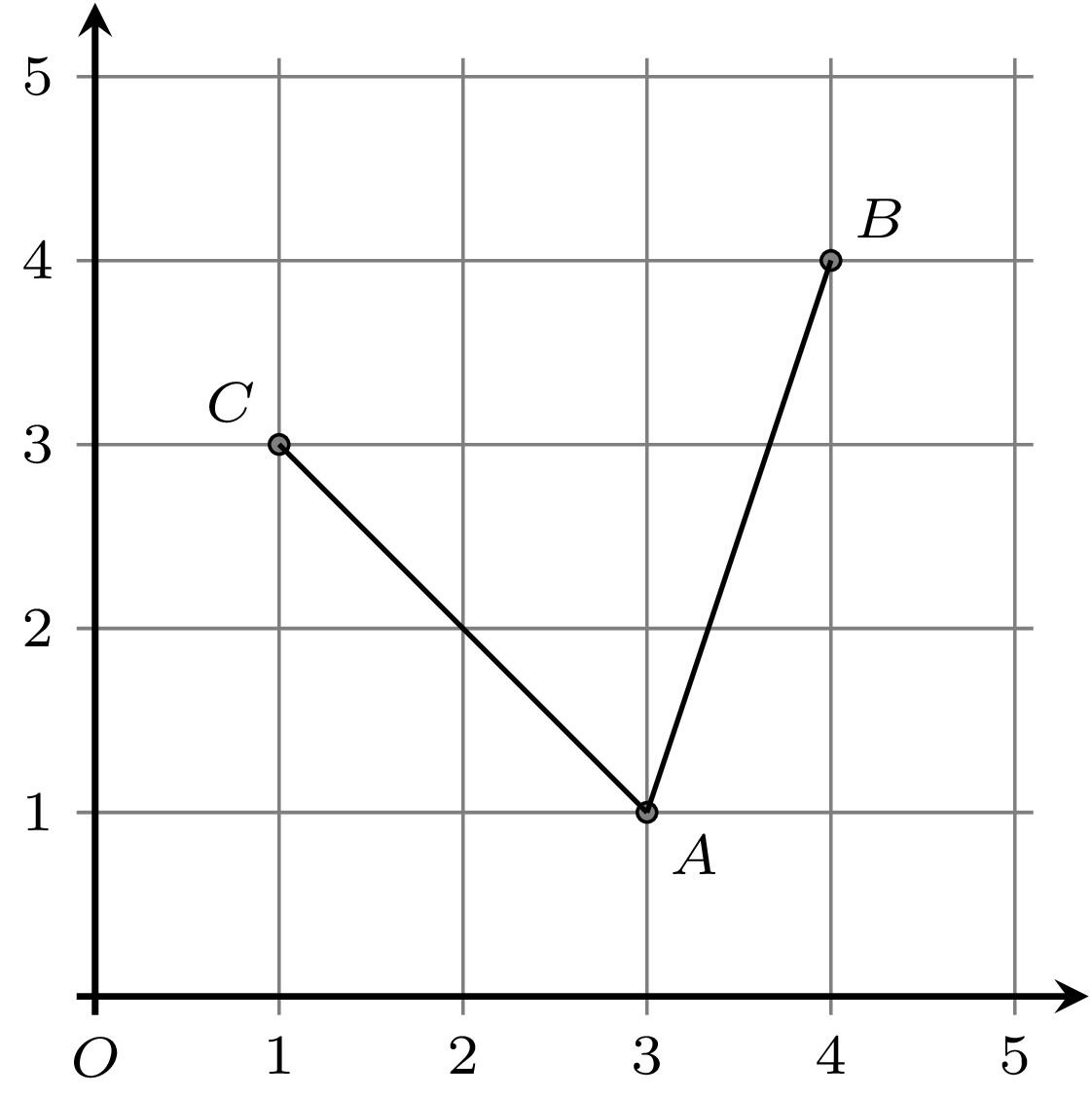
Rys. 1. Muszkieter \(A\) widzi muszkietera \(B,\) jednak nie widzi muszkietera \(C,\) gdyż przeszkadza mu w tym punkt \((2,2)\)
W artykule Nigdy Cię nie zobaczę (\(\Delta_{20}^{12}\)) rozpatrzyliśmy dokładnie ten przypadek i naszkicowaliśmy rozumowanie prowadzące do obliczenia liczby \(6/\pi^2\) jako prawdopodobieństwa (jakże pozytywnego!) zdarzenia, że nasi bohaterowie mają kontakt wzrokowy.
Wykażemy teraz, że nie może być pięciu muszkieterów. (Zrobimy to tylko dlatego, że jesteśmy matematykami i nie możemy żyć bez wykazywania, bo czy ktoś słyszał w ogóle o pięciu muszkieterach?) Załóżmy, że dla \(j=1,2,3,4,5\) dany jest punkt \((m_1^{(j)},m_2^{(j)})\in\mathbb Z^2.\) Każdej liczbie całkowitej \(m\) przyporządkujmy resztę \(0,\) gdy \(m\) jest parzysta, albo resztę \(1,\) gdy \(m\) jest nieparzysta. Ponieważ są cztery możliwe pary reszt, więc istnieją \(j_1\neq j_2\) takie, że odpowiadają im te same układy reszt. Zatem obie liczby \(m_1^{(j_2)}-m_1^{(j_1)},m_2^{(j_2)}-m_2^{(j_1)}\) są parzyste, czyli osoby \(j_1\) oraz \(j_2\) nie widzą się.
Teraz rozważymy ważny literacko przypadek \(k=4.\) Jakie jest prawdopodobieństwo, że każdy z muszkieterów ma na oku wszystkich pozostałych? Możemy założyć, że \(DAR=(0,0),\) natomiast \(AT, PO, AR\) to trzy losowe punkty \((m_1^{(j)},m_2^{(j)})\in\mathbb Z^2\) dla \(j=1,2,3.\) Jeśli wszyscy się widzą, to dla każdej liczby pierwszej \(p\) żaden z wektorów: \[(m_1^{(1)},m_2^{(1)}), (m_1^{(2)},m_2^{(2)}),(m_1^{(3)},m_2^{(3)}),\] \[(m_1^{(2)}-m_1^{(1)},m_2^{(2)}-m_2^{(1)}), (m_1^{(3)}-m_1^{(2)},m_2^{(3)}-m_2^{(2)}), (m_1^{(3)}-m_1^{(1)},m_2^{(3)}-m_2^{(1)})\] nie składa się z obu liczb podzielnych przez \(p\) (gdyż wtedy odpowiedni największy wspólny dzielnik byłby \(\geq p\)). Oznacza to dokładnie tyle, że wektory \[(m_1^{(1)},m_2^{(1)}), (m_1^{(2)},m_2^{(2)}),(m_1^{(3)},m_2^{(3)})\] są różne od \((0,0)\) mod \(p\) oraz są parami różne mod \(p.\) Zatem dla ustalonej liczby pierwszej \(p\) rzeczone prawdopodobieństwo, że wszyscy się ,,\(p\)-widzą”, wynosi \[\frac{(p^2-1)(p^2-2)(p^2-3)}{p^6}.\] Ponieważ dla różnych \(p\) te zdarzenia są jakby niezależne (choć nie potrafimy tego sformalizować dla żadnej liczby muszkieterów \(>2\)), więc prawdopodobieństwo, że wszyscy się widzą, powinno wynosić tyle: \[\prod_{p}\frac{(p^2-1)(p^2-2)(p^2-3)}{p^6}\approx 0{,}0246,\] gdzie iloczyn nieskończony jest po wszystkich liczbach pierwszych \(p,\) a przedstawiona przybliżona wartość została wyznaczona na podstawie początkowych \(10^4\) liczb pierwszych. Użyliśmy programu Mathematica do wygenerowania \(10^6\) czworokątów, przy czym każdorazowo \(m_k^{(j)}\) dla \(k=1,2\); \(j=1,2,3\) jest wybierana z rozkładu jednostajnego na zbiorze \(\{1,2,3,\ldots,10^6\}.\) Wypadło \(24\,862\) czworokątów takich, że wszyscy się widzą.
Czytelnicy, którzy wprowadzone nazwy punktów uznają za nienaturalne, zdecydowanie powinni uzupełnić swoją wiedzę na temat muszkieterów.
Dla \(k=2\) w kwestii wspomnianej niezależności odsyłamy jeszcze raz do artykułu w \(\Delta_{20}^{12}\), a po ścisłe obliczenie prawdopodobieństwa do książki T.M. Apostola, Introduction to Analytic Number Theory, str. 62–64.
Dla Czytelników, którym nieobca jest algebra liniowa, zaznaczmy jeszcze, że każda macierz \(M\) wymiaru \(2\times 2\) o wyrazach całkowitych i wyznaczniku 1 opisuje pewien układ czterech muszkieterów, którzy się wzajemnie widzą. Jeśli bowiem \(k_1,k_2\in\mathbb Z^2\) są kolumnami macierzy \(M,\) to możemy przyjąć: \[DAR=(0,0),\ \ AT=k_1,\ \ PO=k_2,\ \ AR=k_1+k_2.\] Z warunku \(\det M=1\) oraz podstawowych własności wyznaczników wynika, że odpowiednie NWD są równe \(1.\)
Odnośnie prawdopodobieństwa, że losowy układ trzech punktów kratowych to trzej muszkieterowie, to podobnie jak dla \(k=4\) przewidujemy, że wynosi ono \[\prod_{p}\frac{(p^2-1)(p^2-2)}{p^4}\approx 0{,}196,\] i znowu eksperymenty numeryczne to potwierdzają. Nie potrafimy jednak udowodnić nawet tego, że dla \(k=3,4\) rzeczone prawdopodobieństwa istnieją.
To, że w pozornie nieskomplikowanym świecie \(\mathbb Z^2\) dzieje się wiele ciekawych rzeczy, zauważył już klasyk gatunku Wacław Sierpiński w swojej popularnej książeczce O stu prostych, ale trudnych zagadnieniach arytmetyki. Z pogranicza geometrii i arytmetyki (Warszawa 1959). Nasza skromna kontrybucja jest zaledwie wyrazem szczerego zachwytu i fascynacji.
W 1906 roku Sierpiński ulepszył jako pierwszy oszacowanie Gaussa na liczbę \(N(R)\) punktów kratowych w kole \(x^2+y^2\leq R^2\): \(|N(R)-\pi R^2|<CR^{2/3},\) gdzie \(C\) jest stałą dodatnią. W oszacowaniu Gaussa występował wykładnik \(1\) zamiast \(2/3.\)