Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Opublikowany w niniejszym wydaniu Delty artykuł Stanisława Majchrzaka garściami czerpie z klasycznych pojęć geometrii elementarnej. Pojawia się w nim również hasło pęk okręgów, które może być obce nawet co bardziej zaawansowanym naśladowcom Euklidesa. Aby oszczędzić Czytelnikowi przeszukiwania Internetu (który zwłaszcza w polskojęzycznej odsłonie jest w tym zakresie dość ubogi w informacje), prezentujemy tutaj przegląd podstawowych informacji na temat tej wdzięcznej geometrycznej konfiguracji.
Tak jak zostało to już wspomniane w przytoczonym artykule, przykładem pęku okręgów jest rodzina wszystkich okręgów przechodzących przez ustalone dwa punkty \(X\) i \(Y.\) Wówczas prosta \(XY\) jest osią potęgową (patrz Deltoid w \(\Delta^{3}_{12}\)) dowolnej pary okręgów z tej rodziny, którą z tego względu nazywa się czasem okręgami współosiowymi. Oznaczmy ową rodzinę jako \(\mathcal{O},\) a jej wspólną oś potęgową jako \(k.\)
Rys. 1. Okręgi z rodziny \(\mathcal{O}\) narysowane są na czarno, a okręgi z rodziny \(\Omega\) – na czerwono. Dowolny czarny okrąg jest prostopadły do dowolnego czerwonego
Wybierzmy na \(k\) dowolny punkt \(P.\) Poprowadźmy z \(P\) styczną do dowolnego okręgu \(o\in \mathcal{O}\) i niech \(T\) będzie punktem styczności (rys. 1). Wówczas \({PT^2=PX\cdot PY}\) (co wynika z definicji osi potęgowej). Oznacza to, że okrąg \(\omega\) o środku \(P\) i promieniu \(\sqrt{PX\cdot PY}\) jest prostopadły do \(o,\) czyli styczne do tych okręgów w punkcie przecięcia są prostopadłe. Z dowolności wyboru \(o\) okrąg \(\omega\) jest prostopadły do wszystkich okręgów z rodziny \(\mathcal{O}.\) Rodzinę tak skonstruowanych okręgów \(\omega\) dla różnych wyborów punktu \(P\) na prostej \(k\) oznaczmy przez \(\Omega.\)
Można pokazać, że osią potęgową dowolnych dwóch okręgów z rodziny \(\Omega\) jest symetralna \(l\) odcinka \(XY.\) Dlatego \(\Omega\) również nazywana jest rodziną okręgów współosiowych lub też pękiem – tym razem jednak są to okręgi parami rozłączne i dlatego to drugie określenie może być odrobinę mylące. Ogólnie okręgami współosiowymi nazwiemy każdą rodzinę okręgów, dla której istnieje prosta będąca osią potęgową dowolnej pary okręgów z tej rodziny. Jeśli nie można jej powiększyć o żaden dodatkowy okrąg, mówimy o pęku okręgów.
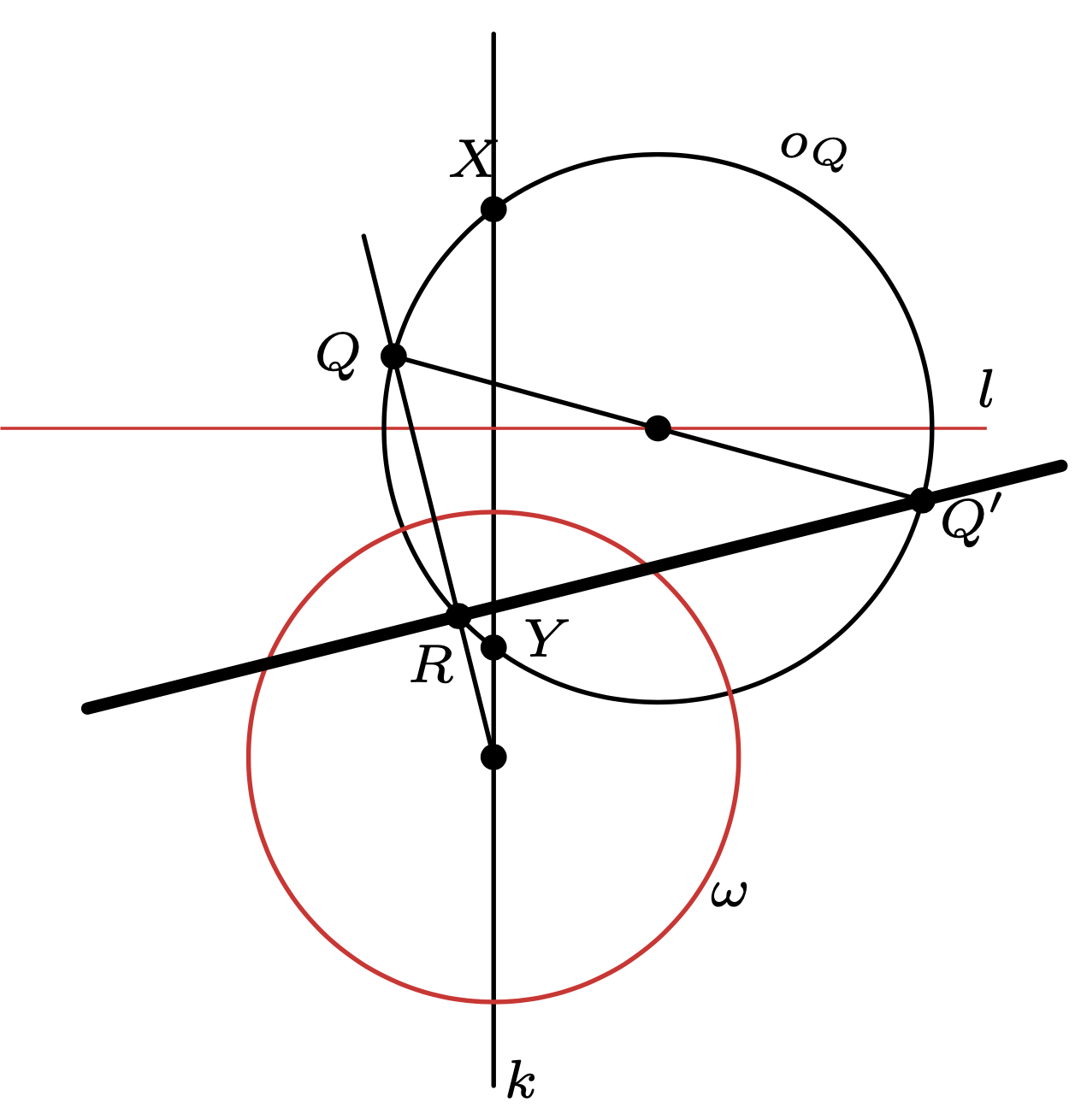
Wybierzmy dowolny punkt \(Q\) i okrąg \(\omega\in \Omega.\) Poprowadźmy biegunową \(Q\) względem \(\omega\) – definicja biegunowej pojawiła się już w artykule Stanisława Majchrzaka. Udowodnimy, że dla różnych wyborów okręgu \(\omega\) utworzone w ten sposób proste przecinają się w jednym punkcie. W tym celu przypomnimy alternatywną definicję biegunowej (patrz KPO w \(\Delta^1_{23}\)) – jest to prosta prostopadła do odcinka łączącego dany punkt ze środkiem okręgu, przechodząca przez obraz inwersyjny tego punktu względem okręgu. Czytelnikom, którym obce jest pojęcie inwersji, a którzy mimo to pragną doczytać ten tekst do końca (co jest godne pochwały!), polecam Deltoid z numeru \(\Delta^5_{13}\) oraz artykuł Michała Miśkiewicza z \(\Delta^7_{14}\). Dla nas istotne będzie jedynie to, że inwersja względem okręgu \(\kappa\) o środku w punkcie \(K\) zachowuje półproste wychodzące z punktu \(K\) oraz okręgi prostopadłe do \(\kappa.\)
Rys. 2. Pogrubiona prosta to biegunowa \(Q\) względem \(\omega\)
Narysujmy teraz okrąg \(o_Q\) opisany na trójkącie \(XYQ.\) Oczywiście \(o_Q\in\mathcal{O},\) zatem \(o\) jest prostopadły do wszystkich okręgów z \(\Omega,\) w tym \(\omega.\) Dlatego obraz inwersyjny \(Q\) względem \(\omega\) to punkt \(R\) przecięcia \(o\) z półprostą ze środka \(\omega\) do \(Q\) (rys. 2). Zaś odpowiednia biegunowa to prosta prostopadła do wspomnianej półprostej, przechodząca przez \(R.\) Oznacza to jednak, że biegunowa ta przechodzi przez punkt \(Q',\) antypodalny do \(Q\) w okręgu \(o_Q\) (gdyż kąt \(QRQ'\) jest prosty). Udowodniliśmy w ten sposób, że biegunowe punktu \(Q\) względem okręgów z rodziny \(\Omega\) przecinają się w punkcie \(Q'\) (zależnym tylko od punktów \(X,\) \(Y\) i \(Q\)).
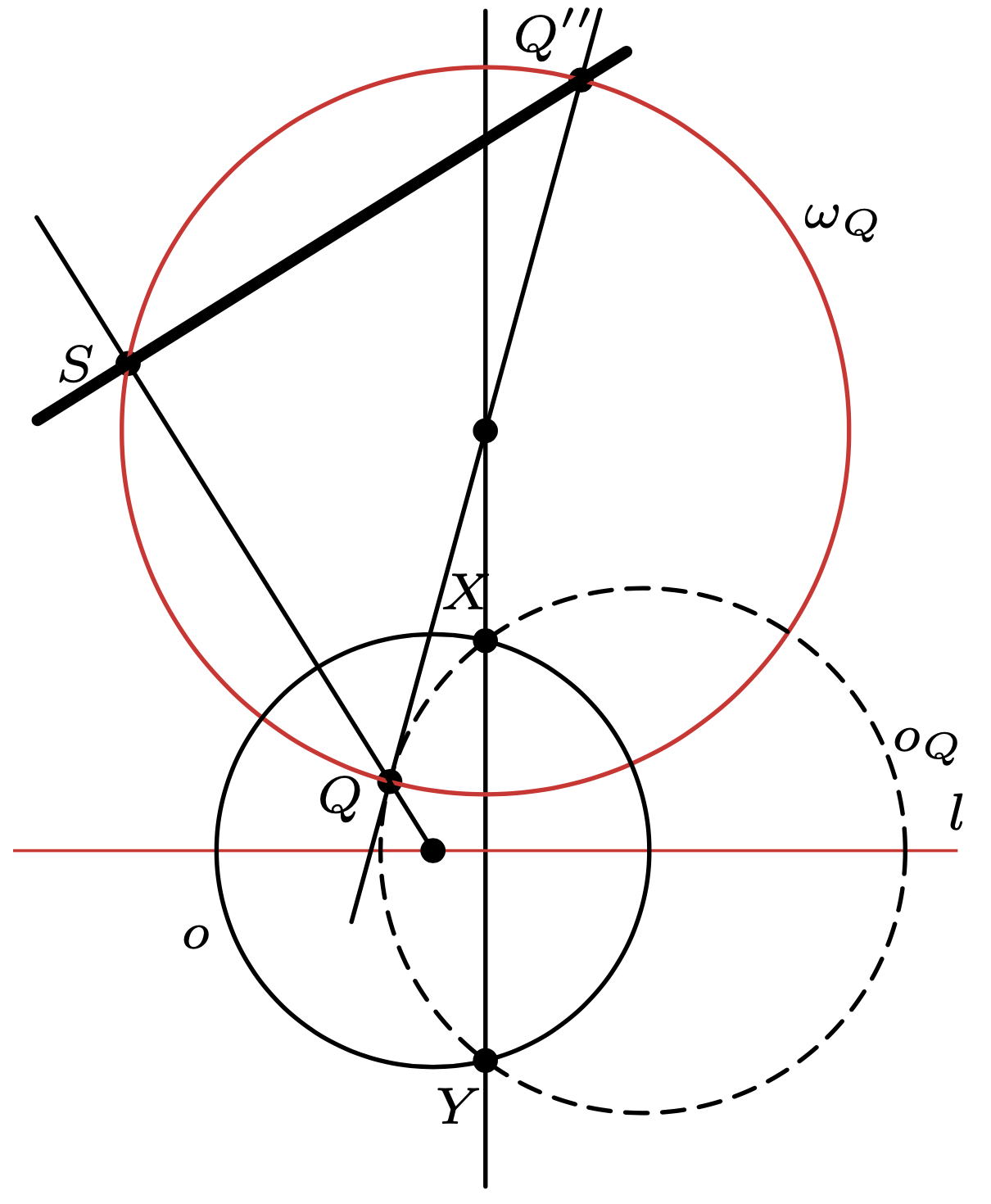
Rys. 3. Pogrubiona prosta to biegunowa \(Q\) względem \(o\)
Udowodnimy teraz, że biegunowe \(Q\) względem okręgów z \(\mathcal{O}\) również przecinają się w jednym punkcie. Pomysł jest dokładnie taki sam – wystarczy udowodnić, że istnieje okrąg \(\omega_Q\) należący do \(\Omega,\) który przechodzi przez \(Q.\) Wówczas wszystkie rozważane biegunowe będą musiały przechodzić przez punkt \(Q''\) antypodalny do \(Q\) w \(\omega_Q.\) Skonstruowanie okręgu \(\omega_Q\) nie jest trudne – potrzeba (i wystarcza), by był on prostopadły również do okręgu \(o_Q.\) Dlatego środek szukanego okręgu \(\omega_Q\) leży na prostej stycznej do \(o_Q\) w punkcie \(Q.\) Środek ten leży też na prostej \(k,\) co pozwala na jego wyznaczenie i w konsekwencji lokalizację punktu \(Q'',\) w którym przecinają się wszystkie biegunowe punktu \(Q\) względem okręgów z \(\mathcal{O}.\)
Na zakończenie wybierzmy w pęku \(\mathcal{O}\) dowolne dwa prostopadłe okręgi i dołączmy do nich dowolny okrąg z \(\Omega.\) Dostaniemy trzy okręgi, z których każde dwa są prostopadłe – ciekawa własność jak na prostopadłość. A czy możliwa jest taka konfiguracja czterech okręgów?