Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Każdy z nas dostał pewnie kiedyś nietrafiony prezent. Puzzle 7+, kiedy mieliśmy 5 lat, skarpetki z Harrym Potterem, chociaż kibicowaliśmy Voldemortowi, czy choinkę zapachową, mimo że nie mamy samochodu. Uśmiechamy się, dziękujemy, ale w głębi duszy już zastanawiamy się, co z tym fantem zrobić. Wyrzucić nie wypada, a zwrócić do sklepu bez paragonu się nie uda. Na pomoc przychodzi jednak Delta! W tym artykule pokażemy, że prezentami można łatwo się powymieniać tak, aby wszyscy byli zadowoleni.
W naszym artykule dla uproszczenia przyjmiemy, że każdy dostał jeden prezent, który chętnie by wymienił (przy dużych rodzinach może być to sporym niedoszacowaniem), oraz że z każdych dwóch prezentów potrafi wskazać, który prezent woli. Każdy umieszcza przed sobą (rozpakowany!) prezent i wykonujemy następującą procedurę:
Krok 1: Każda osoba wskazuje prezent, na którym zależy jej najbardziej.
Krok 2: Znajdujemy cykl, czyli grupę osób, która w kółko wskazuje na swoje prezenty (grupa może składać się z jednej osoby).
Krok 3: Osoby z tej grupy wymieniają się cyklicznie i razem z prezentami za pazuchą opuszczają pokój.
Krok 4: Jeżeli zostały jeszcze jakieś prezenty, wracamy do Kroku 1.
Popatrzmy na przykład. Powiedzmy, że po pierwszym kroku sytuacja wygląda następująco:

Widzimy na przykład, że Dwight chce iPoda, Pam chce dzbanek, a Kevin z wszystkich prezentów najbardziej chce swój masażer do stóp. W drugim kroku musimy znaleźć cykl. Czy jakiś cykl musi powstać? Tak, a aby go znaleźć, wystarczy, że wystartujemy od dowolnej osoby i będziemy podążać za wskazaniami rąk. W ten sposób dostaniemy listę osób, na której w końcu ktoś się powtórzy, np. zaczynając od Ryana, dostajemy ciąg: Ryan, Kelly, Pam, Dwight, Pam… Taka osoba rozpoczyna cykl, w naszym przykładzie złożony z Pam i Dwighta. Jeżeli jest więcej niż jeden cykl (tak jak u nas), to wybieramy dowolny z nich. Weźmy cykl Pam – Dwight. Wykluczamy te dwie osoby oraz ich rzeczy i rozpoczynamy kolejną rundę, w której zasady są takie same: każdy wskazuje, którą z pozostałych rzeczy chciałby mieć najbardziej. W naszym przypadku oznacza to, że wszystkie osoby, które wskazywały iPoda lub dzbanek, muszą wskazać coś innego:
To, który cykl weźmiemy, nie wpłynie na wynik procedury, bo jeżeli są inne cykle, to pozostaną one aż do czasu, gdy je wyeliminujemy – nikomu nie zmieni się najbardziej lubiany przedmiot.

Postępujemy teraz tak jak poprzednio – znajdujemy cykl, wykonujemy zamiany i wykluczamy osoby. Po usunięciu trzech widocznych cykli zostaną nam tylko trzy osoby:

Eliminujemy cykl Kelly – Ryan, i Jim zostaje ze starą koszulą. Finalnie powstały następujące cykle zamian:

Czyli Pam dostaje dzbanek, Dwight iPoda, Toby obraz, Meredith rękawicę, Michael książkę, Kevin masażer itd.
Odporność na wujka Staszka (uncle-Staszek-stability)
Procedura jest prosta, a na dodatek bardzo bezpieczna! Przede wszystkim nikt nie może skończyć z gorszą rzeczą niż ta, z którą zaczął. Jest tak dlatego, że zawsze możemy wskazywać na swoją rzecz – jeżeli zgodziliśmy się na wymianę, to oznacza, że otrzymaliśmy coś lepszego, niż już mieliśmy.
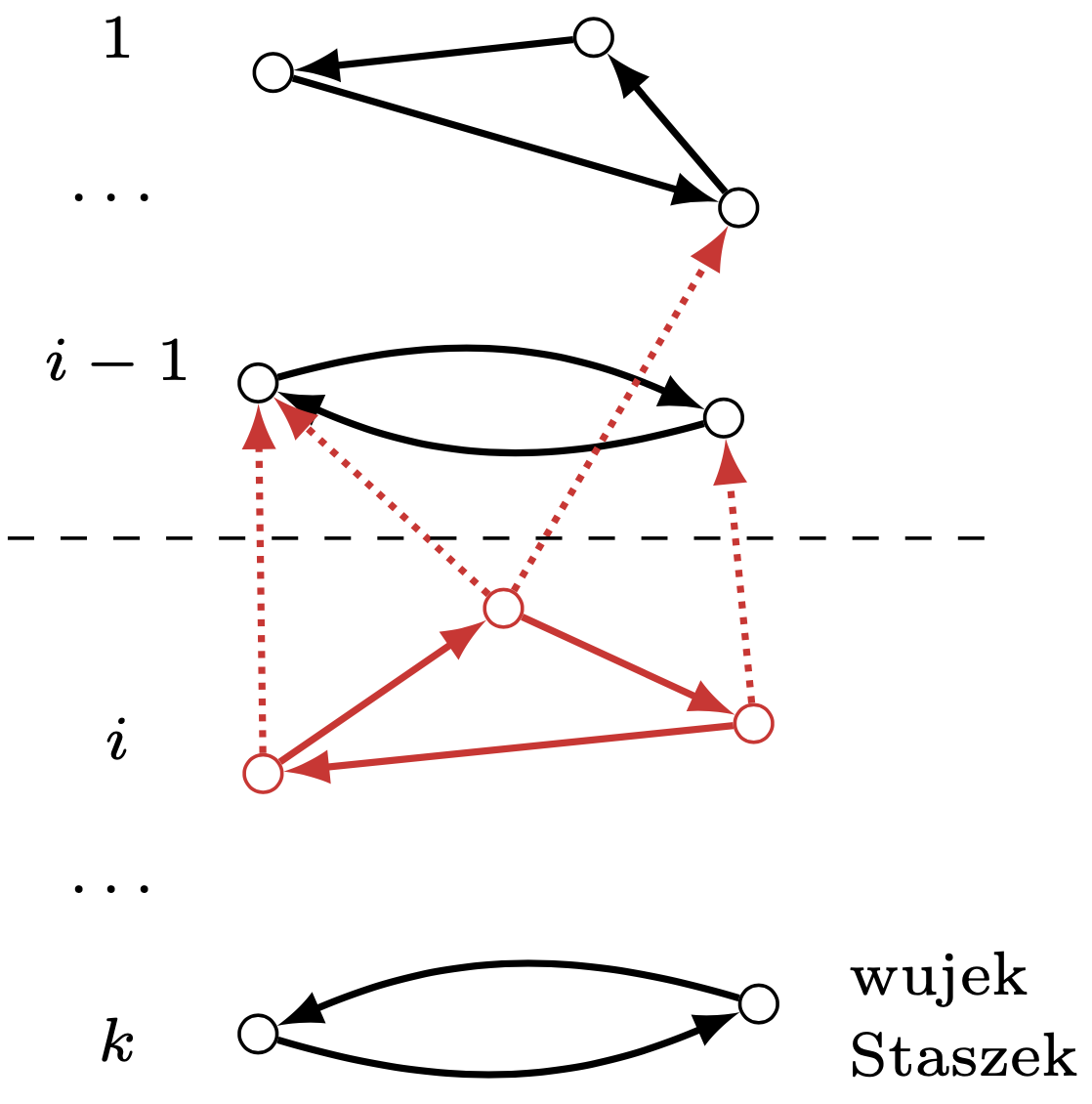
Wiemy, że samo to zapewnienie nie wystarczy, bo zawsze znajdzie się jeden chytry wujek, powiedzmy wujek Staszek, który swoje wie i podejrzliwie podchodzi do tych naukowych wymysłów. Zastanówmy się, czy nasz mechanizm jest odporny na jego potencjalne próby mataczenia.
Najpierw pomyślmy, co się stanie, jeżeli wujek Staszek podpatrzy, kogo wskazują inni, a potem z lekkim opóźnieniem sam wskaże przedmiot. Czy opłaci mu się wskazać inną rzecz niż tę, którą chciałby najbardziej?
Elementy z \(i\)-tego cyklu nigdy nie będą wskazywały elementów, które są eliminowane później, dlatego nie utworzą z nimi cyklu.
Okazuje się, że nie. Załóżmy, że wujek Staszek bez mataczenia zostałby wyeliminowany w \(k\)-tej rundzie. Czy głosując inaczej, mógłby dostać którąś z rzeczy, które usunęliśmy we wcześniejszych rundach? Na pewno nie mógłby dostać nic wyeliminowanego w pierwszej rundzie – wszystkie osoby z pierwszego cyklu dostały to, co chciały najbardziej, i tę rzecz dostaną niezależnie od tego, na co wskazuje palec wujka Staszka (nawet jeżeli wujek Staszek stworzyłby inny cykl, i to jego wybralibyśmy w pierwszej rundzie, to członkowie pierwszego cyklu będą wciąż na siebie wskazywać i w końcu wykonają swoje wymiany). O przedmiotach z pierwszego cyklu możemy zatem zapomnieć. Wujek Staszek nie ma też szans dostać nic wyeliminowanego w drugiej rundzie – osoby z tego cyklu wskazują na siebie nawzajem lub na początku ewentualnie na coś ,,nieosiągalnego” z pierwszego cyklu. Nasz chytry wujek nie utworzy więc z nimi cyklu. Analogicznie wujek Staszek nie dostanie nic z cyklu 3, 4, …, \(k-1.\) Może zatem dostać jedynie coś innego, wyeliminowanego w \(k\)-tej lub kolejnej rundzie, ale przecież tych rzeczy nie woli, skoro nie głosował na nie oryginalnie. Nie ma zatem żadnej motywacji, żeby oszukiwać i nie pokazywać przedmiotu, na którym zależy mu najbardziej. No, może poza przypadkiem, że są to różowe szpilki.
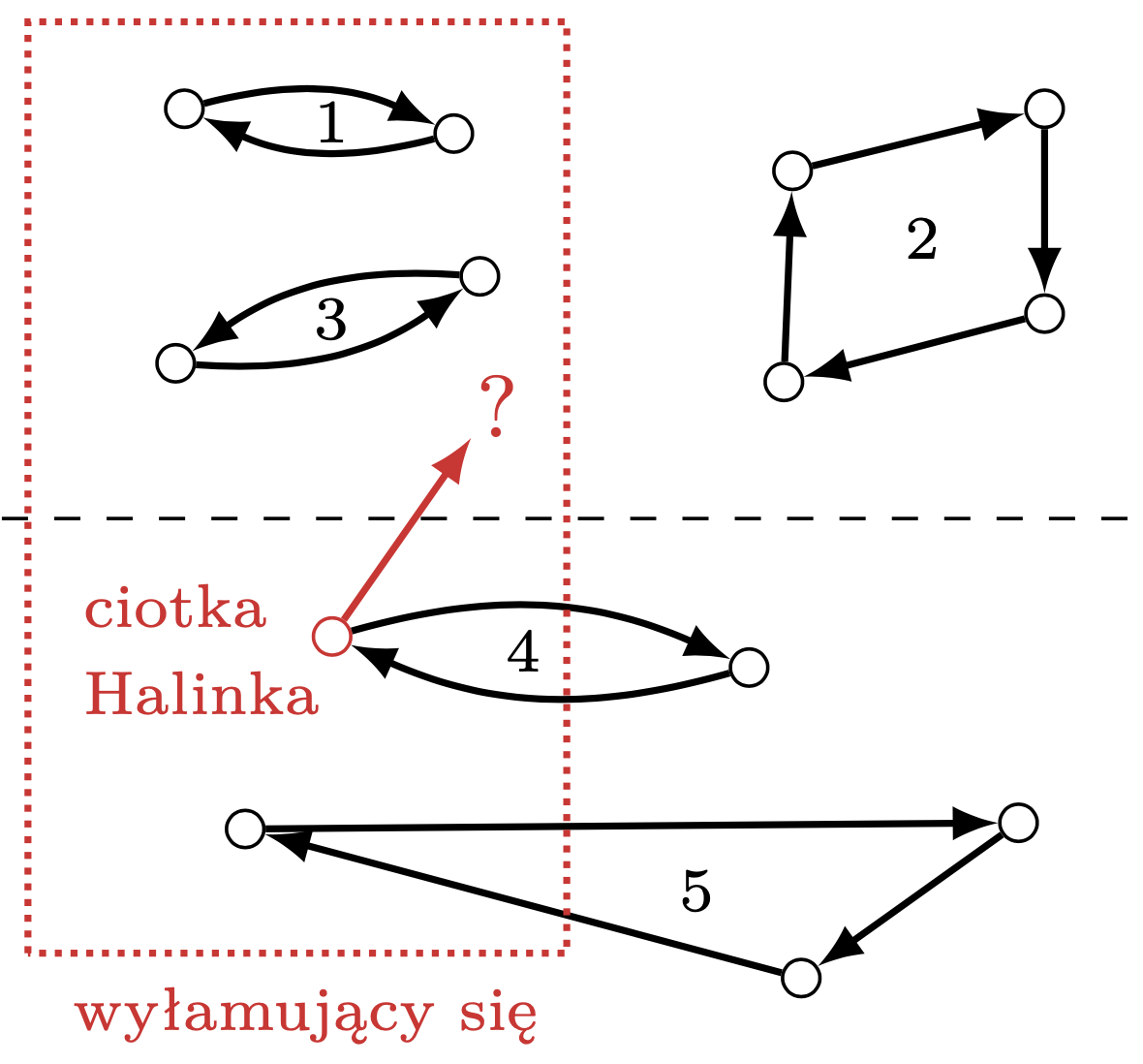
A co, jeśli wujek Staszek podburzy część rodziny, aby zamknęła się w osobnym pokoju i powymieniała prezentami między sobą? Czy mogą na tym zyskać? To znaczy: czy jest możliwe, że nikt z nich na tym nie straci, a przynajmniej jedna osoba zyska? Znowu odpowiedź brzmi: nie!
Gdyby grupa się wyłamała, to aby ktoś zyskał (np. ciotka Halinka), ktoś musiałby stracić. Musiałby to być ktoś eliminowany wcześniej, kto nie chce się zamieniać.
Aby to pokazać, popatrzmy na osobę, która zyskuje i z wyłamującej się grupy była wyeliminowana najwcześniej w naszej oryginalnej procedurze; niech to będzie ciotka Halinka, żona Staszka. Wszystkie osoby z wyłamującej się grupy, które wyeliminowaliśmy przed ciotką Halinką, dostają te same prezenty co w oryginalnej procedurze. Ciotka nie mogła zatem dostać ich przedmiotów. Nie mogła także dostać przedmiotów innych osób wyeliminowanych wcześniej, bo nie są w wyłamującej się grupie i nie ma ich w tym pokoju. Dostała więc przedmiot osoby, która była wyeliminowana po niej albo wtedy co ona, ale tu dochodzimy do sprzeczności, bo w oryginalnej metodzie ciotka dostała najlepszy z takich przedmiotów.
Używając naukowej terminologii, pokazaliśmy, że opisana procedura, znana pod nazwą Top Trading Cycle:
jest odporna na strategię (precyzyjniej, dominant-strategy incentive-compatible), czyli każdej osobie opłaca się postępować zgodnie ze swoimi prawdziwymi preferencjami;
skutkuje takim przypisaniem przedmiotów, które jest jedynym w rdzeniu (core). Oznacza to, że nie istnieje grupa, która wymieniając się tylko między sobą, mogłaby poprawić swoją sytuację (przez co rozumiemy, że nikt nie pogorszy, a przynajmniej jedna osoba polepszy).
Co ciekawe, można pokazać, że wynik naszej procedury jest jedynym przyporządkowaniem odpornym na próby grupowego wyłamania się. Argument za tym jest następujący: jeżeli ktoś z pierwszego wybranego przez nas cyklu dostanie coś innego niż to, na co wskazuje, to uczestnicy pierwszego cyklu będą mogli się wyłamać i wymienić prezentami w swoim gronie – nikt z nich na tym nie straci, a ktoś na pewno zyska. Osoby z drugiego cyklu nie dostaną więc żadnej z rzeczy, którą wyeliminowaliśmy w pierwszym cyklu, więc najlepsze, na co mogą liczyć, to to, na co wskazują. Analogicznie jak poprzednio, argumentujemy, że oni też muszą te rzeczy dostać. Kontynuując to rozumowanie, dochodzimy do wniosku, że przyporządkowanie musi wyglądać tak, jak u nas.
Życzymy owocnych wymian. Wszelkie zażalenia prosimy kierować do potomków Davida Gale’a, który wymyślił opisaną metodę, albo do potomków Lloyda Shapleya oraz Herberta Scarfa, którzy w 1974 roku, czyli dokładnie 50 lat temu, ją opisali.