Uniwersytet im. A. Mickiewicza w Poznaniu
Zajmiemy się tu zadaniami, w których należy wyznaczyć wszystkie liczby naturalne \(n,\) dla których istnieje pewien zadany obiekt. Trzeba pamiętać, że rozwiązanie takiego zadania składa się z dwóch części:
-
w przypadku tych \(n,\) dla których dany obiekt istnieje, wystarczy podać jego konstrukcję albo (co się zdarza w trudniejszych zadaniach) udowodnić jego istnienie metodami pośrednimi, takimi jak na przykład zasada szufladkowa;
-
dla tych \(n,\) dla których nie istnieje dany obiekt, trzeba przeprowadzić dowód jego nieistnienia, najczęściej metodą nie wprost – przez założenie istnienia i doprowadzenie do sprzeczności.
Zwykle jedna z tych dwu części jest łatwiejsza. Pozwala to postawić odpowiednią hipotezę, co często ułatwia rozwiązanie trudniejszej części, ponieważ wiemy już, co chcemy wykazać.
Jako przykład rozwiążemy następujące zadanie z VII Wielkopolskiej Ligi Matematycznej.
Przykład. Nazwijmy grubym prostokąt o bokach \(x\) i \(y\) spełniających warunek \(\frac12x < y<2x.\) Wyznaczyć wszystkie liczby naturalne \(n,\) dla których z kafelków o wymiarach \(1\times1, 1\times2, \ldots, 1\times n\) można ułożyć gruby prostokąt (każdy z kafelków musi być użyty dokładnie jeden raz).
Rozwiązanie. Pole takiego prostokąta jest równe \(\frac12n(n+1),\) dodatkowo jeden z boków ma długość co najmniej \(n.\) W takim razie drugi bok ma długość co najwyżej \(\lfloor\frac12(n+1)\rfloor,\) co jest równe \(\frac12n\) dla \(n\) parzystych. Ale wówczas otrzymany prostokąt nie jest gruby. Udowodniliśmy zatem, że dla parzystych \(n\) taki prostokąt nie istnieje.
W przypadku nieparzystych \(n\) możemy skonstruować gruby prostokąt, tak jak na rysunku poniżej.
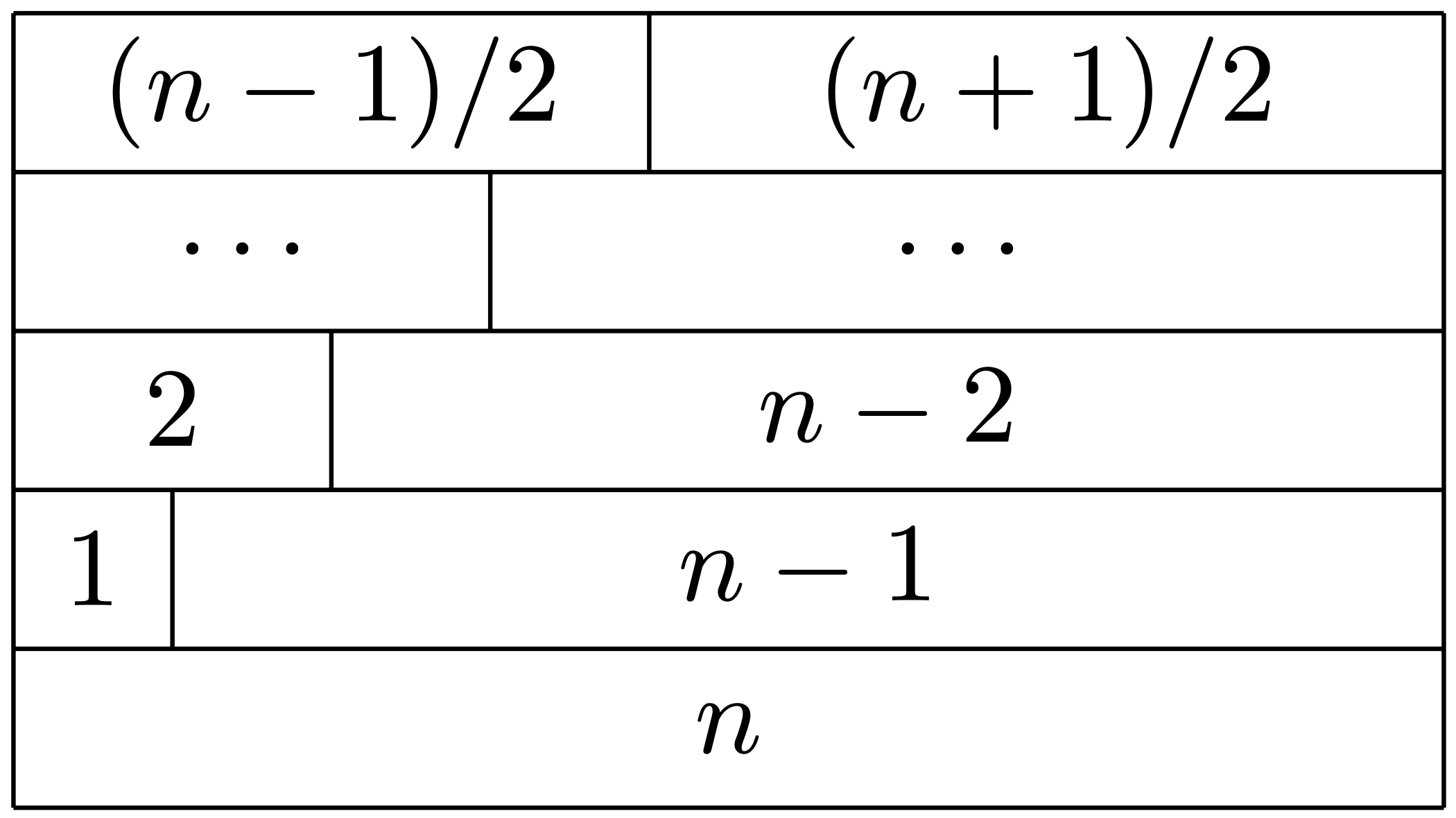
Widoczny tu motyw parzystości często pojawia się w tego typu zadaniach.
Zadania
-
Wyznaczyć wszystkie liczby naturalne \(n\ge4,\) dla których istnieje \(n\)-kąt, którego każdy kąt wewętrzny ma \(90^\circ\) lub \(270^\circ.\)
Wskazówka Każde dwa sąsiednie boki są prostopadłe, więc \(n\ge 4\) musi być parzyste.
-
Dla jakich liczb całkowitych dodatnich \(n\) zbiór \(\{1,2,3,\ldots,2n\}\) można rozbić na dwa rozłączne \(n\)-elementowe podzbiory o jednakowych sumach?
Wskazówka Liczba \(1+2+\ldots+2n=n(2n+1)\) musi być parzysta, więc liczba \(n\) również.
-
Wyznaczyć wszystkie liczby naturalne \(n,\) dla których istnieje \(n\)-ścian wypukły, którego wszystkie ściany są przystającymi trójkątami.
Wskazówka Liczba krawędzi takiego wielościanu jest równa \(\frac 32n,\) więc \(n\) musi być parzyste. Dla \(n=4\) mamy czworościan foremny, a dla parzystych \(n>4\) można skleić podstawami dwa przystające prawidłowe ostrosłupy \((n/2)\)-kątne.
-
Niech \(n\) będzie liczbą nieparzystą. Z \(\frac{n^3-1}2\) niebieskich prostopadłościanów o wymiarach \(1\times1\times2\) i jednego zielonego o wymiarach \(1\times1\times1\) chcemy zbudować sześcian o krawędzi \(n,\) ale środek powstałego sześcianu ma leżeć w środku zielonego klocka. Wyznaczyć wszystkie \(n,\) dla których jest to możliwe.
Wskazówka Zauważmy, że analogiczna konstrukcja na płaszczyźnie jest wykonalna dla każdego nieparzystego \(n.\) Jeśli \(n=4k+1,\) to jako środkową warstwę sześcianu bierzemy konstrukcję z płaszczyzny, a dodatkowo z góry i z dołu dokładamy prostopadłościany \(n\times n\times 2k.\) W przypadku \(n=4k+3\) kolorujemy sześciany jednostkowe sześcianu \(n\times n\times n\) w czarno-białą szachownicę. Niech środkowy sześcianik będzie czarny – wśród pozostałych jest wtedy więcej białych niż czarnych, z czego można wywnioskować, że konstrukcja jest niewykonalna.
-
Znaleźć wszystkie całkowite dodatnie \(n,\) dla których istnieje ciąg \((x_0,x_1,\ldots,x_n)\) o następujących własnościach: \(x_0=0,\) \(x_1+x_2+\ldots+x_n=0\) oraz \(|x_k|=|x_{k-1}+1|\) dla każdego \(k=1,2,\ldots,n.\) (LII OM, zmodyfikowane)
Wskazówka Niech \(s_k=x_1+x_2+\ldots+x_k.\) Po podniesieniu danej w zadaniu równości obustronnie do kwadratu, zsumowaniu stronami dla \(k=1,2,\ldots,n\) i prostych przekształceniach otrzymamy \(2s_n+n+1 = (x_n+1)^2,\) więc \(s_n=0 \iff |x_n+1|=\sqrt{n+1}.\) Wnioskujemy stąd, że \(n=m^2-1\) dla pewnego naturalnego \(m.\) Osiągalności dowodzimy indukcyjnie, rozważając wszystkie możliwe wartości \(x_n.\)
-
Wyznaczyć wszystkie dodatnie liczby całkowite \(n\) o następującej własności: z \(n\) prostokątów o wymiarach \(1\times n, 2\times n, \ldots, n\times n\) można ułożyć kwadrat. (LXXV OM)
Wskazówka Liczba \(\frac 12n^2(n+1)\) musi być kwadratem, więc \(n=2k^2-1\) dla pewnej liczby całkowitej \(k,\) a stąd bok kwadratu ma długość \(kn.\) W celu wykonania konstrukcji można ułożyć \(k^2\) kwadratów \(n\times n.\)
Problem otwarty
-
Na płaszczyźnie znaduje się \(n\) punktów czerwonych, \(n\) zielonych i \(n\) niebieskich. Każda prosta przechodzi albo przez co najwyżej jeden z tych punktów, albo przez dwa punkty jednakowego koloru, albo przez trzy punkty różnych kolorów. Wyznaczyć wszystkie możliwe wartości \(n.\) (Problem autorski, częściowe rozwiązanie w Matematycznym Kalendarzu Adwentowym 2021).
Wskazówka Znana jest mi konstrukcja dla \(n=1,2,3,4\) i nic więcej.