Afiliacja: Wydział Budownictwa i Inżynierii Środowiska, Szkoła Główna Gospodarstwa Wiejskiego w Warszawie
**Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Archimedes z Syrakuz (ok. 287–212 p.n.e.) – jeden z najwybitniejszych umysłów matematycznych w historii. Urodził się i zmarł w Syrakuzach. Poza matematyką zajmował się również fizyką i inżynierią. W swoich czasach wsławił się dzięki wynalazkom mechanicznym – tzw. śrubie Archimedesa do pompowania wody, dźwigni, planetarium (bardzo dokładnie odtwarzającym ruchy ciał niebieskich) oraz maszynom wojennym, które przerażały rzymskich żołnierzy podczas oblężenia Syrakuz (oblężenie to przyniosło śmierć Archimedesowi). Niestety tylko niektóre dzieła Archimedesa przetrwały do naszych czasów. Należy do nich ważny traktat zatytułowany ,,Metoda”, który został ponownie odkryty dopiero w 1906 roku, w Konstantynopolu, praktycznie przez przypadek – w palimpseście powstałym w roku 1229. W tym traktacie Archimedes szczegółowo opisał swoją metodę dźwigni. Historia wspomnianego palimpsestu (zawierającego także inne traktaty Archimedesa) i metody użyte do jego prawidłowego odczytania są przedstawione w bardzo ciekawej książce Reviela Netza i Williama Noela [4].
Największe pomysły cechuje prostota
William Golding
Obliczanie pól figur płaskich i objętości brył, nawet w prostych przypadkach, bywa czasem dość kłopotliwe, np. wtedy, gdy łatwo jest napisać całkę wyrażającą pole figury, ale samo obliczenie tej całki jest niebanalne. Zagadnieniem metod obliczania pól i objętości zajmowało się wielu wybitnych matematyków, począwszy od czasów starożytnych aż po nam współczesne.
W tym artykule przedstawiamy trzy geometryczne podejścia do wyznaczania pól i objętości opracowane w różnych epokach: podejście Archimedesa (III w. p.n.e.), Cavalieriego (XVII w.) oraz Mamikona Mnatsakaniana (XX w.).
Metoda I – podejście Archimedesa. Archimedes uważany jest za jednego z twórców statyki i hydrostatyki. Obliczył on środki ciężkości wielu ważnych figur geometrycznych i brył, między innymi trójkąta, trapezu, dowolnego wycinka paraboli i segmentu paraboloidy obrotowej. Swoje wyniki dotyczące statyki zawarł w dziełach O równowadze płaszczyzn i Kwadratura paraboli.
Prawo dźwigni, sformułowane przez Archimedesa, jest jednym z praw równowagi, należy do statyki i mówi, że:
Wielkości są w równowadze w odległościach odwrotnie proporcjonalnych do ich wag.
Jeżeli po obu stronach dźwigni umieścimy masy, odpowiednio, \(m\) i \(m',\) a odległości ich środków ciężkości od punktu podparcia dźwigni, odpowiednio, \(d_S\) i \(d_{S'},\) są do siebie w stosunku odwrotnie proporcjonalnym do stosunków tych mas: \[\begin{aligned} \frac{d_S}{d_{S'}}=\frac{m'}{m}, \end{aligned}\] to dźwignia pozostaje w równowadze statycznej.
Jeśli przyjmiemy, że obie masy mają tę samą stałą gęstość, to \(m'/m=V'/V,\) gdzie \(V'\) i \(V\) są objętościami mas, odpowiednio, \(m'\) i \(m.\) Zatem \[\begin{aligned} \frac{d_S}{d_{S'}}=\frac{V'}{V}. \end{aligned}\] Gdy rozważamy wyidealizowany problem dwuwymiarowy, objętości \(V'\) i \(V\) zamieniamy na pola \(A'\) i \(A\) dwóch figur płaskich.
Powyższą zasadę można wykorzystać w celu wyznaczania pól i objętości w następujący sposób (por. [2]). Przypuśćmy, że \(R\) i \(S\) to dwa obszary leżące wzdłuż tego samego odcinka osi poziomej (rys. 1). Mając dane pole \(A(S)\) oraz środek ciężkości \(c_S\) obszaru \(S,\) pytamy o pole \(A(R)\) obszaru \(R.\)

Rys. 1
Obszary \(R\) i \(S\) są wypełnione liniami pionowymi, odpowiednio, \(l\) i \(l'\) tak, że każda linia \(l\) (odp. \(l'\)) jest zawarta w obszarze \(R\) (odp. \(S\)), a każdy punkt obszaru \(R\) (odp. \(S\)) należy do dokładnie jednej linii \(l\) (odp. \(l'\)).
Przypuśćmy, że istnieje taka stała \(k,\) że dla każdej pionowej linii w odległości \(x\) od punktu \(O,\) przecinającej obszary \(R\) i \(S\) w odcinkach o długościach \(l\) i \(l',\) odpowiednio, spełniona jest relacja \[\frac{k}{x}=\frac{l'}{l}\,.\] Wówczas z prawa dźwigni wynika, że odcinek \(l\) umieszczony w punkcie \(P,\) w odległości \(k\) od punktu podparcia \(O,\) równoważy odcinek \(l'\) w miejscu, w którym się znajduje.
Zatem jeśli obszar \(R\) zostanie umieszczony tak, aby jego środek ciężkości znalazł się w punkcie \(P,\) to zrównoważy on obszar \(S\) w miejscu, w którym się znajduje, co prowadzi do równania \[\frac{k}{x_S}=\frac{A(S)}{A(R)},\] gdzie \(x_S\) to odległość środka ciężkości \(c_S\) obszaru \(S\) od punktu \(O.\) Znając \(A(S),\) \(x_S\) oraz \(k,\) z powyższego równania obliczamy szukaną wielkość \(A(R).\)
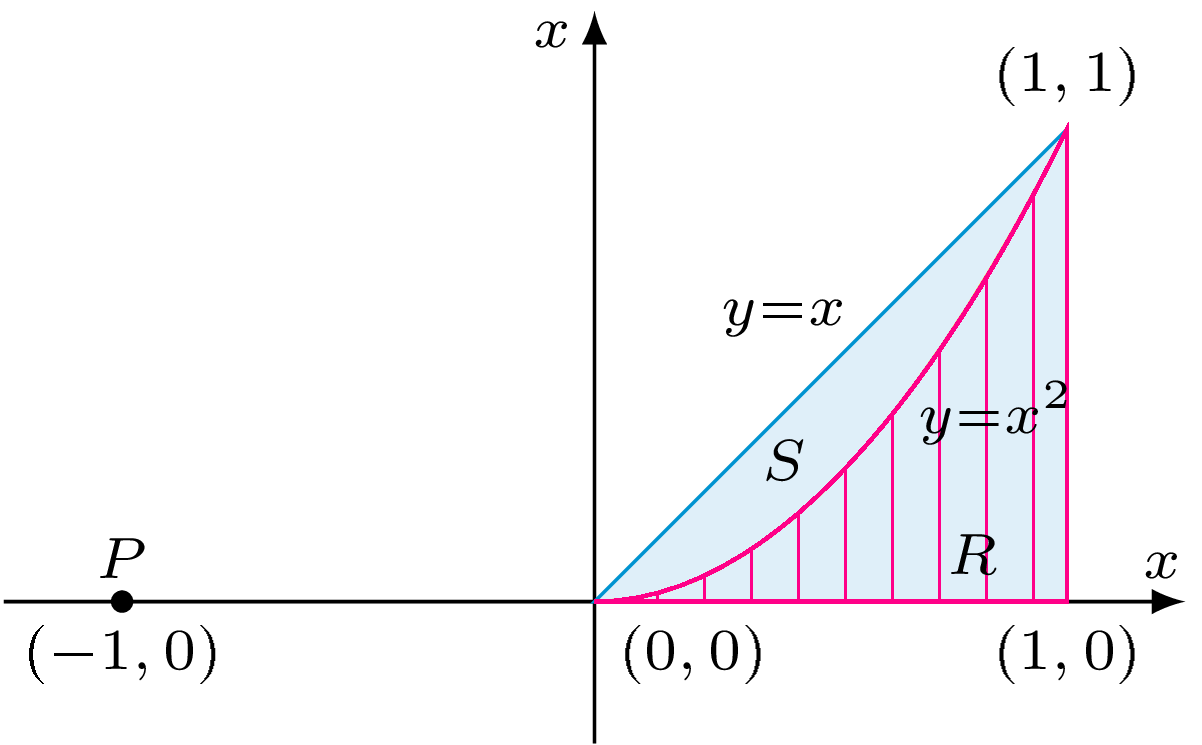
Przykład 1. Obliczenie pola pod parabolą. Weźmy za \(R\) obszar ograniczony przez parabolę \(y=x^2,\) oś \(OX\) oraz prostą \(x=1.\) Niech \(S\) będzie trójkątem o wierzchołkach w punktach \((0,0),\) \((1,0),\) \((1,1),\) którego pole powierzchni wynosi \(A(S)=\frac{1}{2},\) a środek ciężkości ma pierwszą współrzędną \(x_{S}=\frac{2}{3}.\)
Rys. 2
Mamy \(l=x^2,\) a \(l'=x,\) zatem możemy przyjąć \(k=1\) i otrzymujemy \(1 \cdot x^2=x \cdot x.\) Oznacza to (przy założeniu, że oś \(OX\) jest dźwignią podpartą w punkcie \((0,0)\)), że gdybyśmy przesunęli obszar \(R\) pod parabolą tak, aby jego środek ciężkości znalazł się w punkcie \(P\) o współrzędnych \((-1,0),\) to zrównoważyłby on trójkąt w miejscu, w którym się znajduje. Otrzymujemy zatem: \[A(R) = A(S) \cdot x_S = \frac{1}{2} \cdot \frac{2}{3} = \frac{1}{3}.\] W celu wykorzystania tej metody do wyznaczenia objętości brył należy zastąpić długości odcinków polami powierzchni przekrojów poprzecznych. Jako ilustrację przytoczymy jeden z najważniejszych wyników otrzymanych przez Archimedesa.
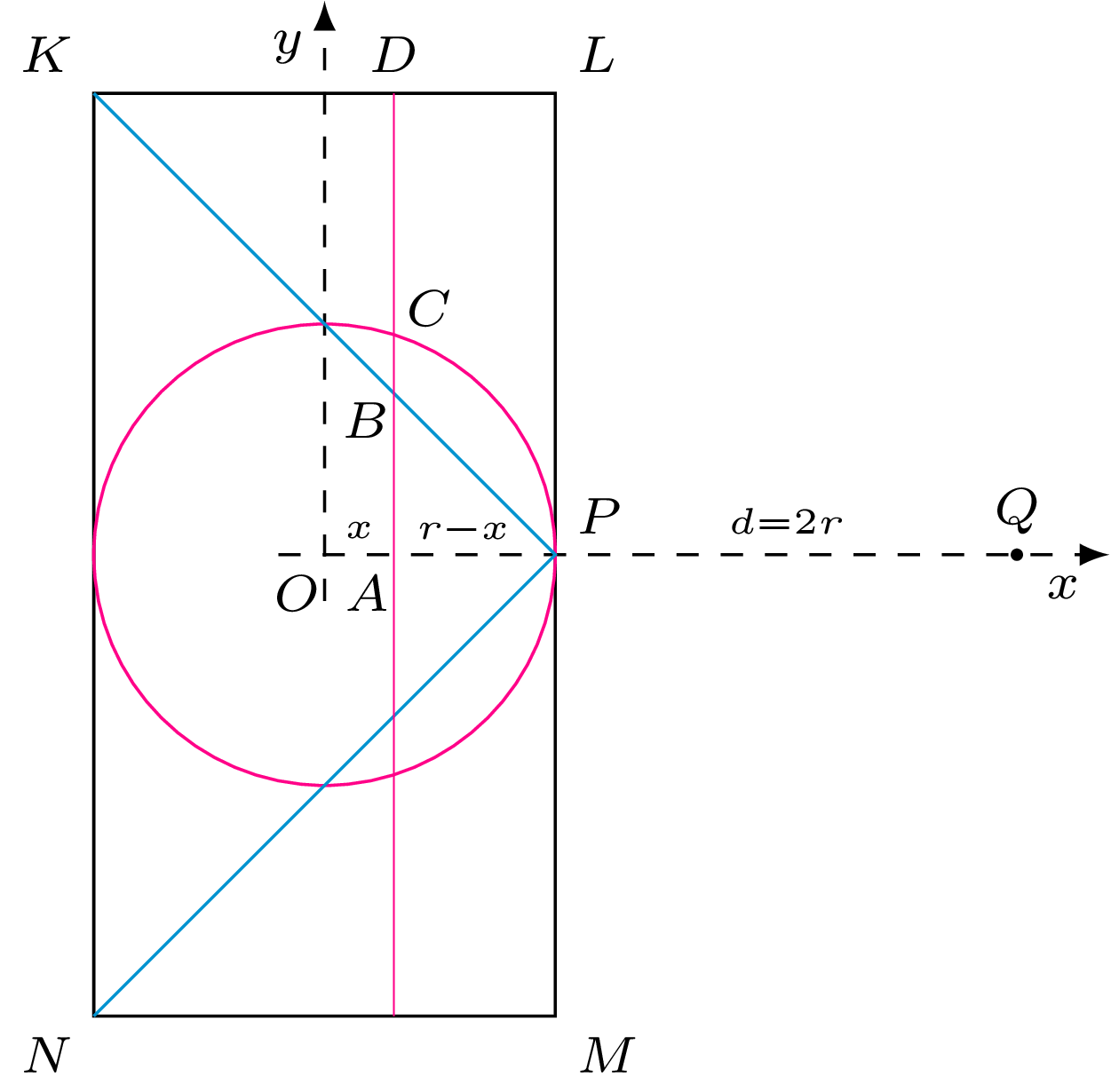
Przykład 2. [2] Obliczenie objętości kuli. Konstrukcję rozpoczynamy od narysowania okręgu \(x^2+y^2=r^2\) przecinającego oś \(OX\) w punkcie \(P=(r,0).\) Następnie rysujemy prostokąt \(KLMN,\) którego środek ciężkości umiejscowiony jest w środku układu współrzędnych. Jego podstawa ma długość \(d=2r,\) a jego wysokość jest równa \(h=2d.\) Rysujemy również trójkąt \(KNP.\) Przez obrót tych figur wokół osi \(OX\) otrzymujemy bryły: kulę \(S,\) stożek \(C\) oraz walec \(Z.\) Zauważmy, że otrzymane bryły zbudowane są z dysków prostopadłych do osi \(OX.\) Dla przykładu, przekrój płaszczyzną prostopadłą do osi \(OX,\) przechodzącą przez punkt \(A=(x,0)\) przecina kulę – tworząc koło \(S_x\) o promieniu \({AC=y=\sqrt{r^2-x^2}},\) stożek – tworząc koło \(C_x\) o promieniu \(AB=r-x\) oraz walec – tworząc koło \(Z_x\) o promieniu \(AD=d=2r.\) Przeprowadźmy rachunki: \[\begin{aligned} d \cdot [A(S_x)+A(C_x)] &= \pi d \cdot [y^2+(r-x)^2] \\&= \pi d \cdot [(r^2-x^2)+(r^2-2rx+x^2)] \\&= \pi d \cdot (2r^2-2rx) \\&= \pi d^2 \cdot (r-x) \\&= (r-x) \cdot A(Z_x). \end{aligned}\] Mamy zatem \[d \cdot [A(S_x)+A(C_x)] = (r-x) \cdot A(Z_x),\] co oznacza, że jeśli przyjmiemy, że oś \(OX\) jest dźwignią z podparciem w punkcie \(P,\) oraz umieścimy koła \(S_x\) i \(C_x\) w punkcie \(Q=(3r,0),\) to razem zrównoważą koło \(Z_x\) w miejscu, w którym się znajduje. To prowadzi do wniosku, że jeśli kulę \(S\) oraz stożek \(C\) umieścimy tak, aby ich środki ciężkości znalazły się w punkcie \(Q,\) to razem zrównoważą one walec \(Z\) w miejscu, w którym się znajduje. Zatem zasada dźwigni implikuje relację: \[2r \cdot [V(S)+V(C)] = r \cdot V(Z).\] Podstawiając znane objętości \(V(C)=\frac{1}{3} \pi d^3\) oraz \(V(Z) = \pi d^3,\) obliczamy objętość kuli o promieniu \(r\): \[V(S) = \frac{1}{6} \pi d^3 = \frac{4}{3} \pi r^3.\] Metoda II – podejście Cavalieriego. Bonaventura Cavalieri spopularyzował swoją metodę w dwóch pracach, Geometria indivisibilibus z 1635 roku oraz Exercitationes geometricae sex z 1647 roku. Opiera się ona na zasadzie znanej jako twierdzenie Cavalieriego.
Rys. 3
Bonaventura Francesco Cavalieri (1598–1647). Włoski matematyk i astronom. Studiował na uniwersytetach w Pizie i w Bolonii. Był uczniem Galileusza. Zajmował się głównie geometrią. Jako pierwszy zaczął stosować metody nieskończenie małych elementów do obliczania pól powierzchni i objętości
Twierdzenie Cavalieriego. [2] Jeśli dwie bryły mają tę własność, że ich przekroje wszystkimi płaszczyznami równoległymi do jednej, z góry ustalonej płaszczyzny mają te same pola, to te bryły mają równe objętości. Jeśli przekroje na równych wysokościach są w stałym stosunku, to objętości tych brył również są w tym stosunku.
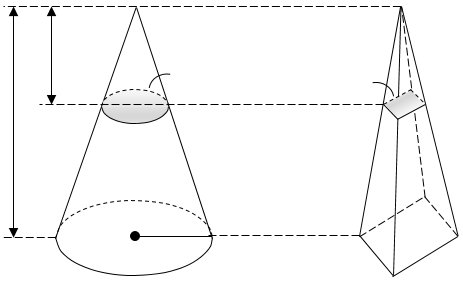
Przykład 3. Obliczenie objętości stożka. Zauważmy najpierw, że możemy łatwo wyznaczyć pola powierzchni przekrojów stożka oraz ostrosłupa na dowolnej wysokości. Mamy (patrz rys. 4) \[A(C_x)=\frac{\pi r^2 x^2}{h^2} \ \ \ \textrm{oraz} \ \ \ A(P_x)=\frac{x^2}{h^2}.\]
Rys. 4
Ponieważ stosunek tych pól na dowolnej wysokości jest stały i nie zależy od \(x,\) \[\frac{A(C_x)}{A(P_x)}=\pi r^2,\] więc, na podstawie twierdzenia Cavalieriego, stosunek objętości brył jest taki sam. Znając objętość ostrosłupa (\(V(P)=\frac{1}{3}\cdot 1 \cdot h\)), łatwo teraz wyznaczamy objętość stożka: \[\frac{V(C)}{V(P)}=\pi r^2 \Rightarrow V(C)=\pi r^2 V(P) = \frac{1}{3} \pi r^2 h.\] Metoda III – podejście Mamikona. Przytoczymy tu tylko jeden z całej bogatej kolekcji pomysłów Mamikona Mnatsakaniana, odsyłając zainteresowanego Czytelnika do dalszej lektury [1]. Przedstawiony tu pomysł ma źródło w prostej obserwacji. Zastanówmy się, ile wynosi pole powierzchni pierścienia zawartego pomiędzy dwoma okręgami o wspólnym środku, w którym długość cięciwy większego okręgu, stycznej zewnętrznie do mniejszego okręgu, wynosi \(a\)?
Więcej przykładów zastosowania zasady Cavalieriego można znaleźć w artykule Jarosława Górnickiego z \(\Delta^{1}_{12}.\)
Mamikon Mnatsakanian (po lewej), Tom M. Apostol (po prawej)Mamikon Mnatsakanian (1942–2021). Ormiański fizyk, który na metodę „całkowania wizualnego” wpadł w trakcie studiów. Pomysł ten jednak przez wiele lat nie został zauważony i doceniony. Dopiero w trakcie pobytu Mamikona w USA prof. Tom M. Apostol dostrzegł w jego metodzie potencjał i wspólnie zaczęli się nią zajmować i rozwijać.
,,Jako nauczyciel rachunku różniczkowego z ponad 50-letnim stażem i autor kilku podręczników na ten temat byłem zdumiony, gdy dowiedziałem się, że wiele standardowych problemów w rachunku różniczkowym można łatwo rozwiązać za pomocą innowacyjnego podejścia wizualnego, które nie korzysta ze wzorów”. – Tom M. Apostol

Rys. 5
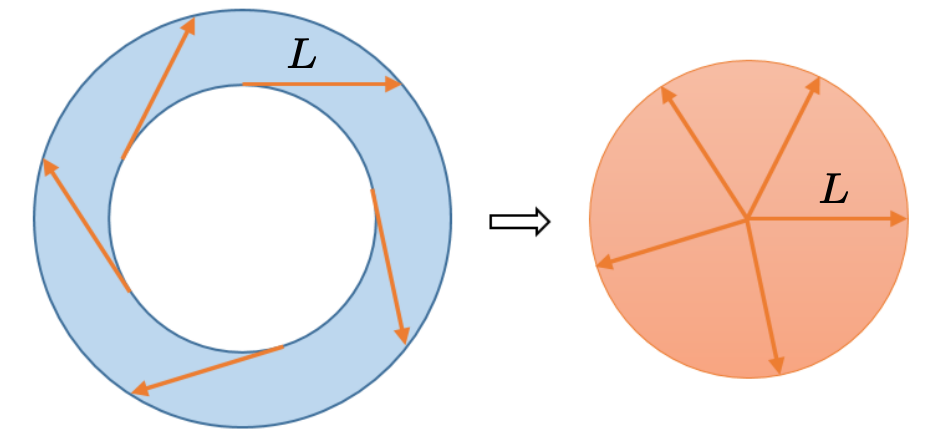
Rys. 6
Standardowy rachunek jest prosty, odpowiedź to (przy oznaczeniach z rys. 5): \[\pi R^2 - \pi r^2 = \pi (R^2-r^2)=\pi \biggl(\frac{a}{2}\biggr)^2,\] gdzie w ostatniej równości skorzystaliśmy z twierdzenia Pitagorasa. Pole to nie zależy zatem od promieni okręgów, a jedynie od długości cięciwy stycznej do wewnętrznego okręgu. Obserwacja ta stała się przyczynkiem do rozważań na temat wyznaczenia tego pola w inny sposób.
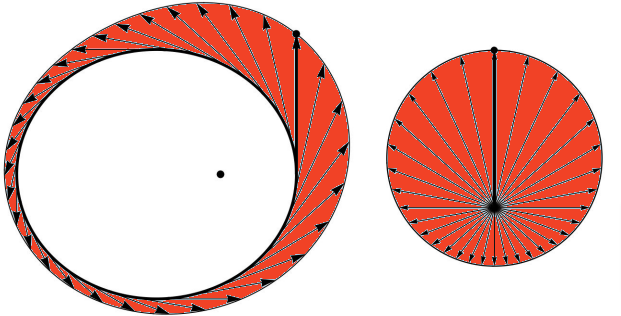
Wyobraźmy sobie, że połowa wspomnianej cięciwy jest wektorem \(\vec L\) o długości \(L=\frac{a}{2},\) który obracamy wokół mniejszego okręgu tak, że w każdym miejscu jest on styczny do tego okręgu. Wykonując pełny obrót, zakreślimy cały interesujący nas obszar. Mamikon spostrzegł, że po zaczepieniu wszystkich tych wektorów w jednym punkcie otrzymamy koło o promieniu równym długości obracanego wektora i polu równym \(\pi L^2\) (rys. 6). Pole to jest oczywiście równe polu rozważanego pierścienia (zauważmy, że to rozumowanie nie wymaga użycia twierdzenia Pitagorasa).
Powyższą sytuację możemy zinterpretować w ramach mechaniki Newtona jako szczególny przypadek ogólniejszego twierdzenia mówiącego o tym, że hodograf prędkości ruchu po elipsie w polu Newtonowskim z centrum w jednym z jej ognisk jest okręgiem o promieniu \(r=\frac{v_P+v_A}{2},\) gdzie \(v_P\) i \(v_A\) są prędkościami, odpowiednio, w peryhelium i aphelium elipsy (por. artykuł William Rowan Hamilton i hodograf z \(\Delta^{9}_{24}\)).
Mamikon uogólnił swoje spostrzeżenie, formułując następujące twierdzenie, dotyczące krzywych niekoniecznie zamkniętych, do których wektory styczne nie muszą mieć tej samej długości w każdym punkcie krzywej.
Twierdzenie Mamikona (postać ogólna). Pole zakreślenia stycznego dla dowolnej gładkiej krzywej jest równe polu jego pęku stycznego.
Twierdzenie Mamikona pozostaje prawdziwe również dla krzywych w przestrzeni trójwymiarowej.
Przez ,,zakreślenie styczne” rozumiemy obszar złożony z rozłącznych odcinków stycznych do krzywej, a przez ,,pęk styczny” – zbiór powstały przez takie przesunięcie owych odcinków, by pozostały one rozłączne i pokryły się punkty ich styczności do krzywej. Na rysunku 6 widzimy przykład zakreślenia stycznego do wewnętrznego okręgu po lewej stronie i jego pęk styczny po prawej stronie rysunku. Wspomniany wyżej hodograf prędkości dla ruchu po elipsie w polu Newtonowskim jest następnym przykładem pęku stycznego, także będącego okręgiem (rys. 7). Tym razem zakreślenie styczne składa się z wektorów o różnej długości.
Rys. 7
W celu zilustrowania powyższego twierdzenia pokażemy dwa przykłady dotyczące krzywych na płaszczyźnie.
Przykład 4. Wyznaczenie pola powierzchni pomiędzy wykresem funkcji eksponencjalnej a osią odciętych w granicach od minus nieskończoności do ustalonego \(x\). W celu zrozumienia rozwiązania ważne jest zauważenie, że dla funkcji \(y=e^{\frac{x}{b}}\) odcinek łączący dowolny punkt \((x,0)\) na osi odciętych z miejscem przecięcia tej osi ze styczną do wykresu funkcji w punkcie \((x,e^{\frac{x}{b}})\) ma stałą długość równą \(b\) (patrz rys. 8).
\(y\!=\!e^{x/b}\) \(b\) \(b\) \(b\) \(x\)
Rys. 8
Rys. 9
Zauważmy, że przenosząc wszystkie odcinki styczne do miejsca przecięcia stycznej do krzywej w punkcie \((x, e^\frac{x}{b})\) z osią \(OX,\) zapełniamy trójkąt prostokątny o przyprostokątnych długości \(b\) i \(e^{\frac{x}{b}}.\) Trójkąt ten wypełnia zatem połowę pola powierzchni pod wykresem, które wobec tego musi być równe \(2 \cdot \frac{1}{2} b e^\frac{x}{b}=b e^\frac{x}{b}.\)
Przykład 5. Wyznaczenie pola powierzchni pomiędzy wykresem funkcji \(x^n\) a osią odciętych w granicach od zera do ustalonego \(x\). Dla ustalenia uwagi przyjmiemy \(n=2\) (dla innych potęg rozumowanie jest analogiczne).
Zauważmy, że figura, której pola szukamy, zawarta jest w prostokącie o bokach równych \(x\) i \(x^2,\) zatem na pewno jest to część pola powierzchni tego prostokąta równego \(P = x^3.\) Archimedes jako pierwszy obliczył, przy pomocy metody dźwigni, że pole to wynosi \(\frac{1}{3}P\) (patrz przykład 1). Poniżej pokażemy, jak można uzyskać ten wynik w dość prosty sposób, oparty na elementarnym podejściu geometrycznym. To, co będzie nam potrzebne, to fakt, że styczna do paraboli w punkcie o odciętej \(x\) przecina oś \(OX\) w punkcie o odciętej \(\frac{x}{2}\) \((=x-\frac{x^2}{2x})\). Styczna ta dzieli naszą figurę na dwie części, na rysunku oznaczone przez \(S\) oraz \(T.\) Figura \(S\) powstaje przez narysowanie wszystkich odcinków stycznych do paraboli i kończących się na osi \(OX.\)
Metodę Mamikona można również odnaleźć w artykule W którą stronę jechał rower? z \(\Delta^8_{22}\).
Przedłużmy teraz odcinki tworzące obszar \(S\) do przecięcia z osią \(OY\) (rys. 9b). Z wcześniejszej obserwacji dotyczącej ich punktu przecięcia z osią \(OX\) wynika, że w ten sposób każdy z nich został przeskalowany przez \(t=2.\) Z twierdzenia Mamikona i twierdzenia o jednokładności wynika, że zakreskowany obszar ma pole powierzchni równe \(t^2A(S)=4A(S).\) Dlatego obszar pod osią \(OX\) ma powierzchnię równą \(3A(S).\) Jednocześnie obszar ten jest przystający do obszaru \(T.\) Zatem \(A(T)=3A(S)\) oraz \(4A(T) = P,\) skąd otrzymujemy \({A(T\cup S) = \frac{1}{3}P=\frac{1}{3}x^3}.\)
Literatura
[1] T. M. Apostol, M. A. Mnatsakanian, New Horizones in Geometry, The Mathematical Association of America, 2012.
[2] C. H. Edwards, The Historical Development of the Calculus, Springer-Verlag, NewYork, 1979.
[3] P. Lynch, Mamikon’s Visual Calculus and the Hodograph, Mathematics Today, April 2022, 212-214.
[4] R. Netz, W. Noel, Kodeks Archimedesa, Magnum, 2002.
Wszystkie powyższe obliczenia można łatwo otrzymać, korzystając z rachunku całkowego w ujednolicony sposób, dość mechanicznie i prawie bez żadnego nakładu myślowego. Pokazuje to siłę rachunku całkowego, w którym rozumowanie jest ukryte w ,,czarnej skrzynce”, a do nas należy włożenie danych, ,,pokręcenie korbką” i wyjęcie gotowego wyniku. Jednak ten brak naoczności Leibnizowskiej wersji rachunku różniczkowego i całkowego był jedną z przyczyn, dla których Isaac Newton napisał Principia w języku geometrii starożytnych i geometrycznej wersji tegoż rachunku. Dzisiaj, w świecie mechanizacji myślenia, w którym palec (od naciskania klawiszy lub ekranu) boli nas często bardziej niż głowa, przypomnienie wartości piękna, prostoty i głębi rozumowań geometrycznych staje się coraz cenniejsze, nie tylko w dydaktyce matematyki i fizyki.