Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Wyobraźmy sobie następującą sytuację: w Zaczarowanym Lesie żyje sobie \(n>1\) krasnoludków i każdy wychodzi rano do pracy. Przemieszczają się one wzdłuż ustalonych prostych, cały czas poruszając się w tym samym kierunku i ze stałą prędkością. Wiadomo, że ich trasy krzyżują się w sposób maksymalny – to znaczy, że każdy ma na swojej drodze \(n-1\) skrzyżowań z pozostałymi (i w związku z tym, żadne trzy proste nie przecinają się w jednym punkcie). Jak jednak wiadomo z pewnej bajki, krasnoludki są istotami niezwykle towarzyskimi – powiemy zatem, że krasnoludek jest szczęściarzem, gdy spotka na swojej drodze wszystkie pozostałe. Wówczas okazuje się, że jeśli choć dwa krasnoludki są szczęściarzami, to wszystkie nimi są! Jak można w ogóle podejść do dowodu takiego zaskakującego faktu? Osoby nieprzepadające za geometrią zapewne zechciałyby od razu wszystko sparametryzować i zagłębić się w rachunkach. Okazuje się jednak, że istnieje pewne bardzo ładne i szokująco elementarne rozumowanie.
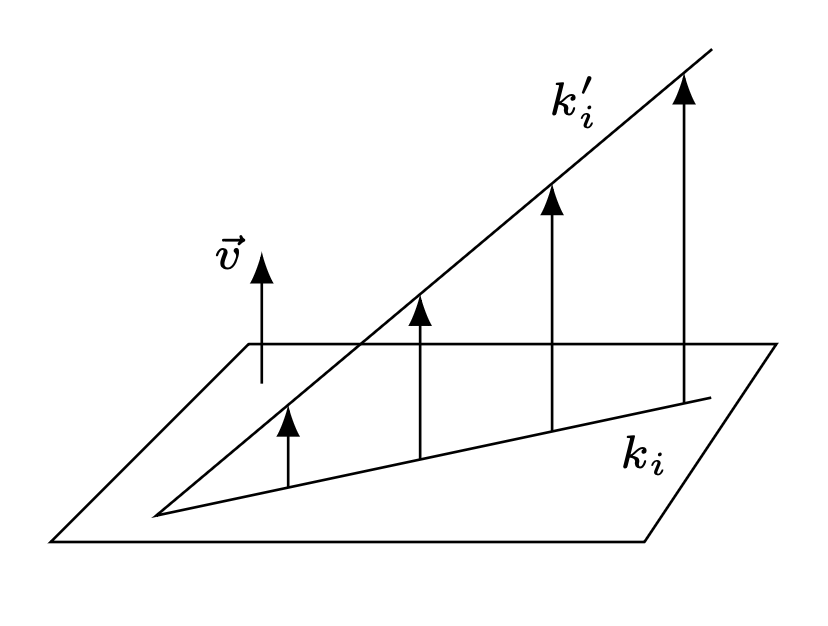
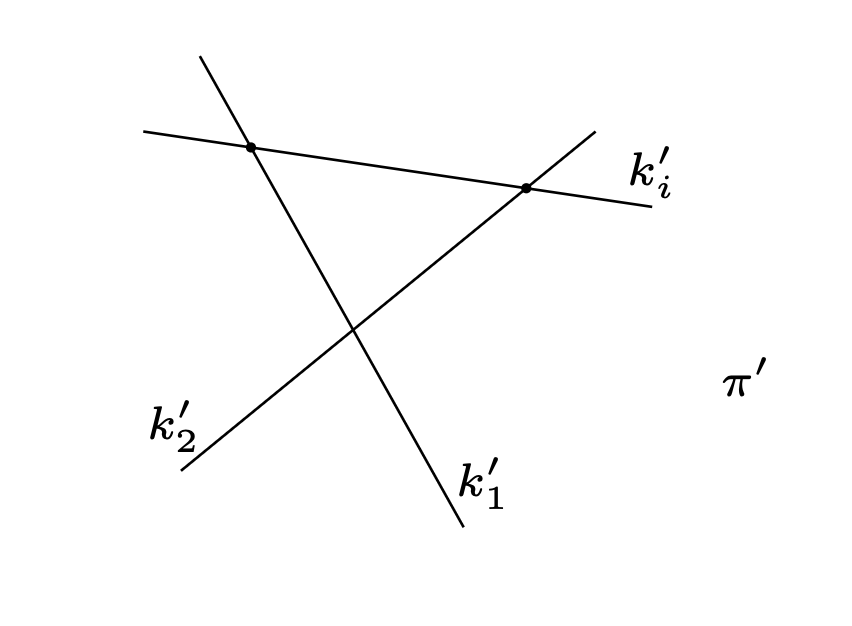
O dziwo, aby rozwiązać ten dwuwymiarowy problem, użyteczne jest odklejenie się od płaszczyzny \(\pi\) Zaczarowanego Lasu i ucieczka w trójwymiarową przestrzeń! Dorysujmy dodatkowy wektor czasowy ustawiony prostopadle do płaszczyzny \(\pi.\) Przyjmujemy, że czas jest skierowany w górę, jak na rysunku obok. Upływ czasu jest jednakowy dla wszystkich krasnoludków (uprzedzam fizyków – pomijamy tu efekty relatywistyczne). Trasa \(k_i\) każdego krasnoludka staje się wówczas prostą \(k_i'\) w trójwymiarze. Jeżeli chcemy zobaczyć, gdzie krasnoludki znajdują się w danej chwili, to sprawdzamy, gdzie reprezentujące ich proste przecinają poziomą płaszczyznę odpowiadającą tej chwili w czasie, czyli na właściwej wysokości. Oczywiście krasnoludki spotykają się wtedy i tylko wtedy, gdy znajdują się w tym samym miejscu, w tym samym czasie – z punktu widzenia naszych „podniesionych” prostych, wtedy i tylko wtedy, gdy proste te się przecinają. Wiemy, że istnieją takie dwie proste, powiedzmy \(k_1'\) i \(k_2',\) które przecinają wszystkie pozostałe „primowane” proste. Popatrzmy więc na płaszczyznę \(\pi'\) wyznaczoną przez \(k_1'\) i \(k_2'.\) Dowolna prosta \(k_i'\) przecina się z \(k_1'\) oraz \(k_2'\) w dwóch różnych punktach, a więc jest zawarta w \(\pi'.\) W związku z tym dowolne dwie proste \(k_i'\) i \(k_j'\) leżą w \(\pi',\) co oznacza, że się przecinają lub są równoległe. Zauważmy jednak, że nie mogą być równoległe – w przeciwnym przypadku, proste \(k_i, k_j \subset \pi\) nie miałyby punktu wspólnego, co przeczyłoby treści. Kończy to zatem dowód.
Rozumowanie to można pociągnąć znacznie dalej! Czy umiesz pokazać, Drogi Czytelniku, że przez cały czas trwania marszu wszystkie krasnoludki są współliniowe?
Opisany powyżej fakt znany jest jako Problem Czterech Podróżnych (zauważmy, że rozwiązanie korzystało jedynie z tylu krasnoludków – pierwszego, drugiego, \(i\)-tego oraz \(j\)-ego). Główne piękno tego rozumowania polega na tym, że aby rozwiązać problem płaski, uciekliśmy w trójwymiar. Przypatrzmy się kilku geometrycznym (i nie tylko!) sytuacjom, w których pojawia się ten elegancki motyw.
Nieco geometrii olimpijskiej
Rozpatrzmy następujące zadanie. Pojawiło się ono na Obozie Naukowym OMG (poziom OM) w \(2015\) roku.
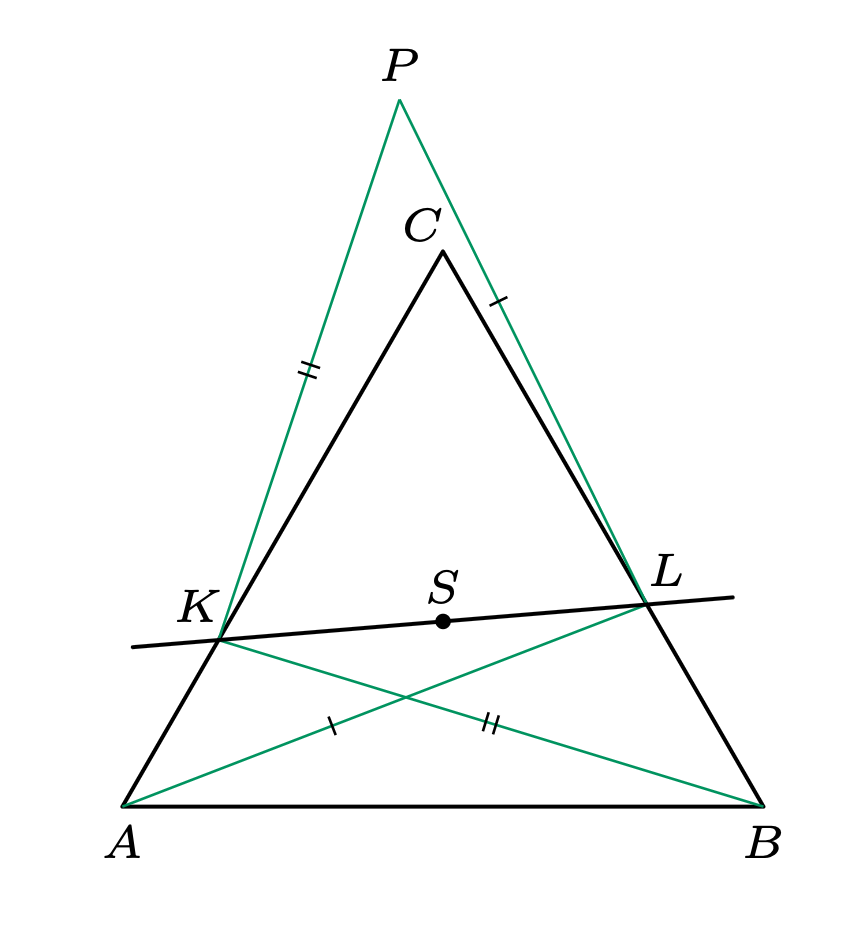
Zadanie. Dany jest trójkąt równoboczny \(ABC\) o środku ciężkości \(S.\) Prosta \(l\) przechodzi przez \(S.\) Niech \(K\) i \(L\) to przecięcia \(l\) z odcinkami \(AC\) i \(BC,\) odpowiednio. Punkt \(P\) spełnia warunki \(AL=PL\) oraz \(BK=PK.\) Udowodnij, że odległość punktu \(P\) od prostej \(l\) jest stała, niezależna od doboru początkowej prostej \(l\) przez \(S.\)
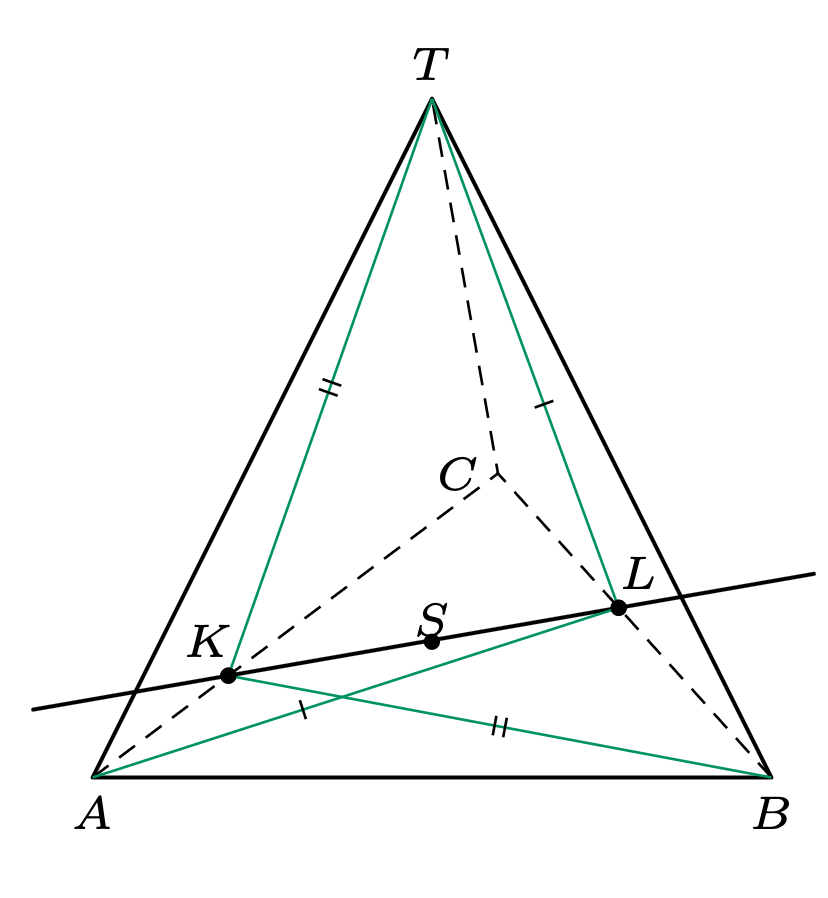
Problem ten jest zaskakująco ciężki, póki trzymamy się kurczowo geometrii płaskiej (przed dalszym czytaniem, zachęcam do podjęcia wyzwania!). Zadanie jednak niemalże trywializuje się po dorysowaniu jednego punktu w trójwymiarze. Niech \(T\) będzie takim punktem w przestrzeni, że \(ABCT\) jest czworościanem foremnym. Wówczas z symetrii tego czworościanu uzyskujemy \(PL=AL=TL\) oraz \(PK=BK=TK.\) Na mocy cechy bok-bok-bok mamy więc \(\triangle KLP \equiv \triangle KLT,\) czyli odległość \(P\) od \(KL\) (a więc i od \(l\)) jest taka sama co odległość \(T\) od \(l.\) Ta jednak pokrywa się z wysokością czworościanu, która oczywiście nie zależy od wyboru prostej \(l.\) Koniec.
Dla tych, którzy powiedzieliby: „po co takie sztuczki, przecież to oczywiste, jak się wpisze w układ współrzędnych”, proponuję spojrzeć na następujący problem.
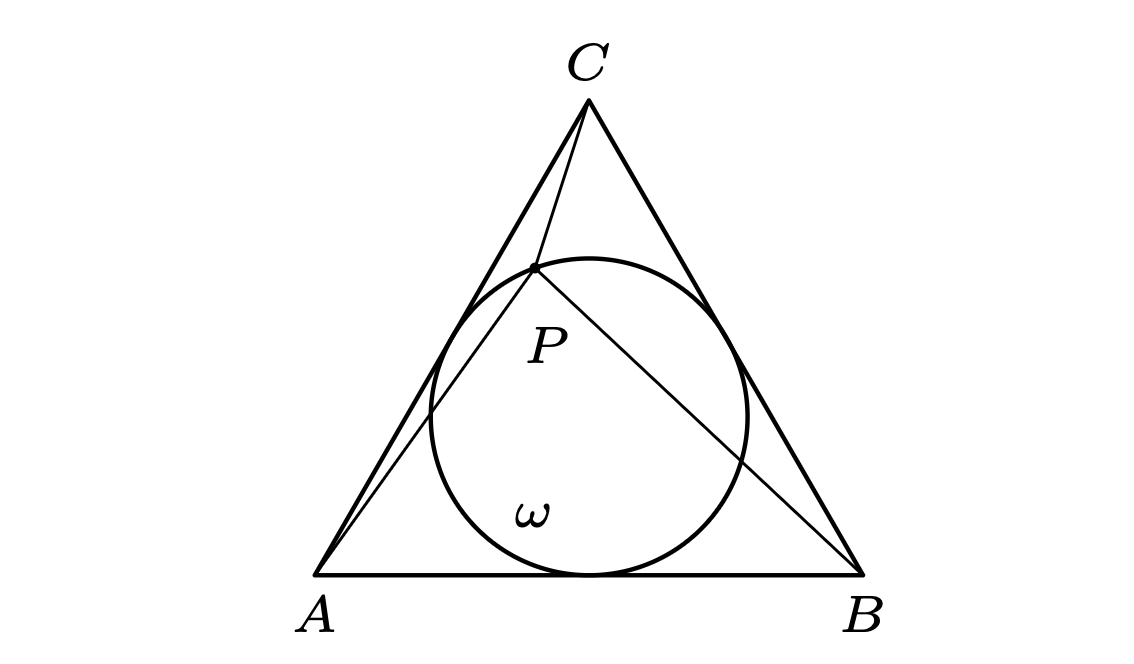
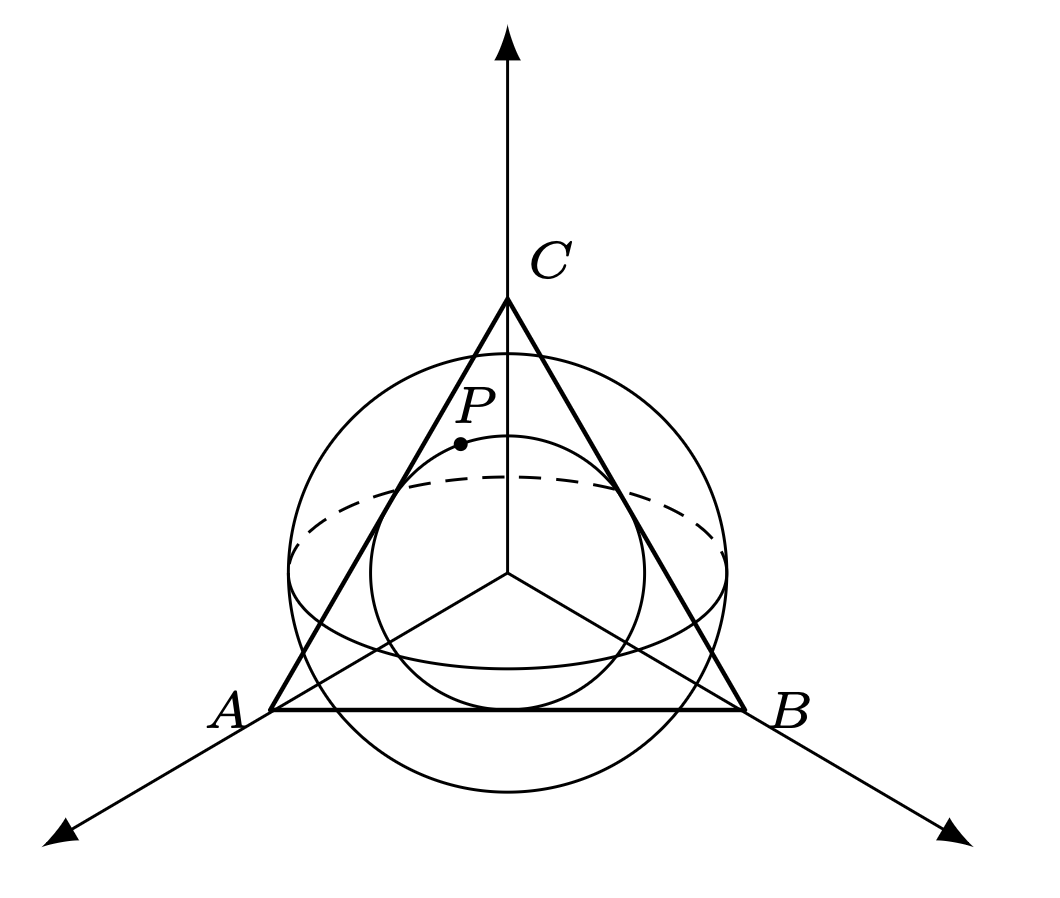
Zadanie. Okrąg \(\omega\) jest wpisany w trójkąt równoboczny \(ABC.\) Punkt \(P\) jest zmieniającym położenie punktem na okręgu \(\omega.\) Udowodnij, że wartość wyrażenia \(AP^2+BP^2+CP^2\) jest stała.
Co w tym niezwykłego? Bierzemy dwie osie, przypisujemy punktom współrzędne i liczymy, prawda? Zachęcam do spróbowania – jak nie robi się tego sprytnie, to rachunki wyjdą (może jeszcze nie najgorsze na świecie, ale) przynajmniej brzydkie. Sztuczka z ucieczką w \(3\)D może być niezwykle przydatna nawet w rozwiązaniach obliczeniowych: Rozpatrzmy trójwymiarowy układ współrzędnych. Wierzchołki trójkąta umieśćmy w punktach \((0,0,1),\) \((0,1,0),\) \((1,0,0)\) – oczywiście daje to trójkąt równoboczny zawarty w płaszczyźnie \(x+y+z=1.\) Czym wówczas jest okrąg \(\omega\)? Jest to przecięcie pewnej sfery o środku w \((0,0,0)\) z tą płaszczyzną (jaki jest jej promień \(R\)?). Innymi słowy, jeśli \(x_P,y_P,z_P\) są współrzędnymi punktu \(P \in \omega,\) to \(x_P^2+y_P^2+z_P^2 = R^2\) jest stałą wartością. Możemy zatem łatwo obliczyć: \[\begin{gathered} AP^2+BP^2+CP^2\\ \begin{split} & = ((x_P-1)^2 + y_P^2 + z_P^2) + (x_P^2 + (y_P-1)^2 + z_P^2) + (x_P^2 + y_P^2 + (z_P-1)^2) \\ & = 3(x_P^2+y_P^2+z_P^2) - 2(x_P+y_P+z_P) + 3 \\ & = 3 \cdot R^2 - 2 \cdot 1 + 3 = 3R^2+1, \end{split} \end{gathered}\] co oczywiście jest stałe. Widzimy zatem, jak użyteczne jest myślenie poza „pudełkiem” zwanym płaszczyzną. Szach-mat!
To samo rozumowanie można zastosować dla dowolnego okręgu o środku będącym środkiem trójkąta \(ABC\) – przykładowo dla okręgu opisanego.
Think bigger
Zanim przejdziemy dalej, do bardziej skomplikowanych konfiguracji, chciałbym wspomnieć o pewnym ważnym, intuicyjnym bycie, zwanym formalnie przestrzenią rzutową. Ile razy zdarzyło się nam stwierdzić, że „dwie proste przecinają się”, zapominając o przypadku, że mogą być równoległe? W tego typu konfiguracjach wygodnie by było uznawać, że proste równoległe również się przecinają, ale w nieskończoności. Intuicja ta prowadzi nas do wspomnianej płaszczyzny rzutowej.
Definicja. Przez płaszczyznę rzutową rozumiemy płaszczyznę z dorzuconymi punktami w nieskończoności (niewłaściwymi), zwanymi kierunkami prostych – każda prosta przechodzi przez swój kierunek, który jest taki sam dla prostych doń równoległych. Ponadto przyjmujemy, że wszystkie punkty w nieskończoności leżą na jednej prostej w nieskończoności (niewłaściwej).
Płaszczyzna z dorzuconym tylko jednym punktem w nieskończoności również jest sensownym bytem – po prostu nie na nasze potrzeby. W ramach ciekawostki powiem, że twór ten nazywa się (w geometrii) płaszczyzną inwersyjną lub (w analizie) sferą Riemanna.
Twór ten jest niezwykle wygodny, gdyż na płaszczyźnie rzutowej dowolne dwie różne proste mają dokładnie jeden punkt wspólny i przez dowolne dwa różne punkty przechodzi dokładnie jedna prosta. Ponadto byt ten można łatwo rozszerzyć do trzech wymiarów: każda prosta dostaje jeden kierunek (wspólny dla wszystkich prostych równoległych), kierunki prostych współpłaszczyznowych leżą na jednej prostej niewłaściwej (wspólnej dla płaszczyzn równoległych), wszystkie proste niewłaściwe leżą na jednej (jedynej!) płaszczyźnie niewłaściwej. Przez resztę artykułu przyjmuję, że zajmujemy się właśnie przestrzenią rzutową (dzięki czemu nie trzeba będzie rozpatrywać przypadków). Zaczniemy od ślicznego dowodu tzw. twierdzenia Monge’a:
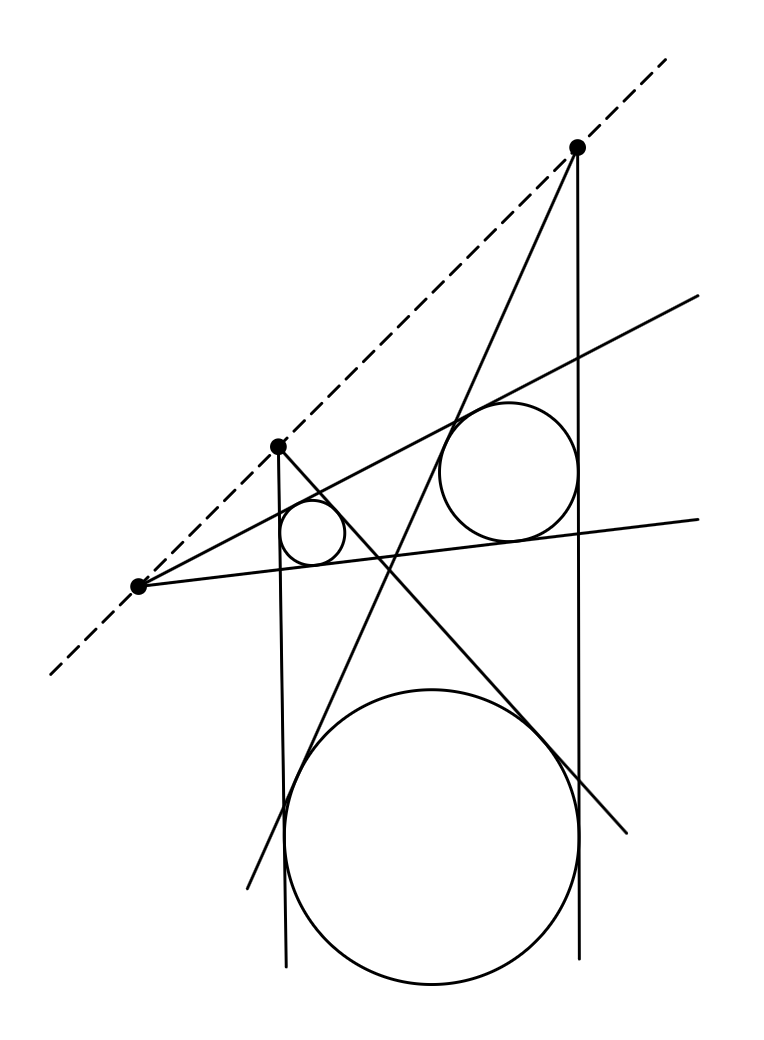
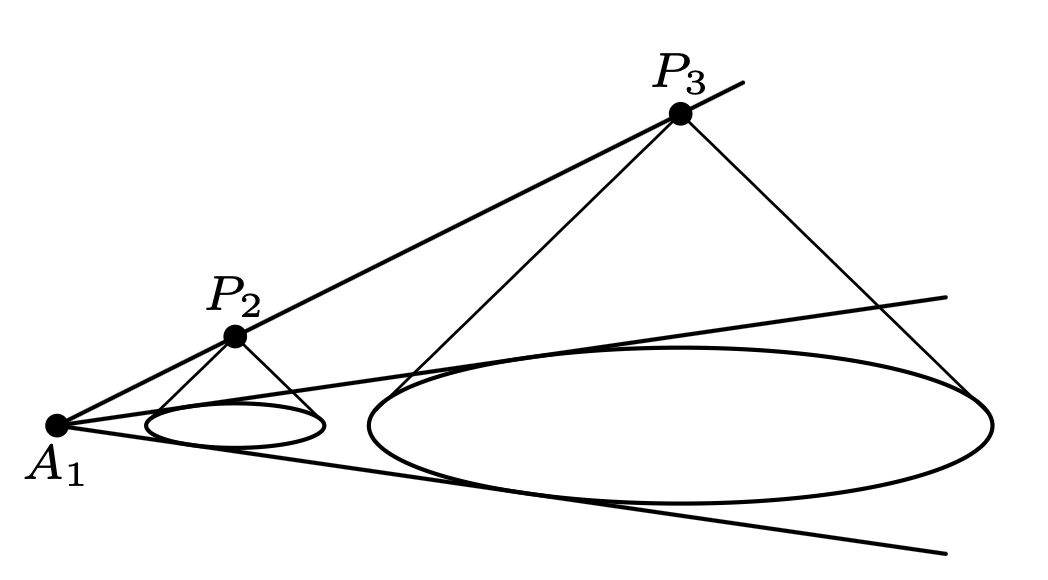
Twierdzenie. Dane są trzy okręgi, \(o_1, o_2, o_3,\) rozłączne zewnętrznie. Niech \(A_1\) to punkt przecięcia wspólnych stycznych zewnętrznych do okręgów \(o_2\) i \(o_3.\) Analogicznie definiujemy \(A_2\) oraz \(A_3.\) Wówczas punkty \(A_1,\) \(A_2,\) \(A_3\) leżą na jednej prostej.
Klasyczny dowód tego faktu wymaga znajomości twierdzenia o składaniu jednokładności. Nie byłoby to jednak w duchu tego artykułu! Robimy inaczej: rozważamy podobne stożki \(s_1,\) \(s_2,\) \(s_3,\) których podstawami są okręgi \(o_1,\) \(o_2,\) \(o_3,\) odpowiednio. Niech ponadto \(P_1,\) \(P_2,\) \(P_3\) będą odpowiednimi wierzchołkami tych stożków, przy czym leżą one wszystkie po tej samej stronie płaszczyzny \(\pi\) zawierającej nasze okręgi. Rozważmy jednokładność o środku w \(A_1\) przenoszącą \(o_2\) na \(o_3.\) Przeniesie ona \(s_2\) na \(s_3\) (przez podobieństwo), a więc \(P_2\) na \(P_3.\) Stąd \(A_1\) leży na prostej \(P_2P_3.\) Analogicznie uzasadniamy, że punkty \(A_2\) i \(A_3\) leżą odpowiednio na prostych \(P_3P_1\) i \(P_1P_2.\) Punkty \(P_1,\) \(P_2,\) \(P_3\) leżą na pewnej płaszczyźnie \(\pi'\) (jeśli są współliniowe, wybieramy dowolną płaszczyznę, która je zawiera). Wówczas punkty \(A_1,\) \(A_2,\) \(A_3\) leżą na \(\pi\) (z definicji) oraz na \(\pi'\) (bo każda z prostych \(P_1P_2,\) \(P_2P_3,\) \(P_3P_1\) zawiera się w \(\pi'\)). Dlatego punkty te leżą w przecięciu płaszczyzn \(\pi\) oraz \(\pi'.\) Płaszczyzny jednak zawsze przecinają się wzdłuż prostej – kończy to zatem dowód.
Co by się stało, gdybyśmy przyjęli, że dwa spośród punktów \(P_1,\) \(P_2,\) \(P_3\) leżą po jednej stronie \(\pi,\) a pozostały po drugiej?
Na zakończenie udowodnimy jeden z najbardziej znanych faktów geometrii rzutowej – twierdzenie Desargues’a; uogólnimy je przy okazji na trzeci wymiar.
Twierdzenie. Dane są dwa trójkąty \(ABC\) i \(A'B'C'\) w \(\mathbb{R}^3.\) Wówczas proste \(AA',\) \(BB'\) i \(CC'\) przecinają się w jednym punkcie wtedy i tylko wtedy, gdy punkty przecięcia prostych \(BC \cap B'C' = P,\) \(CA \cap C'A' = Q\) i \(AB \cap A'B' = R\) istnieją i leżą na jednej prostej.
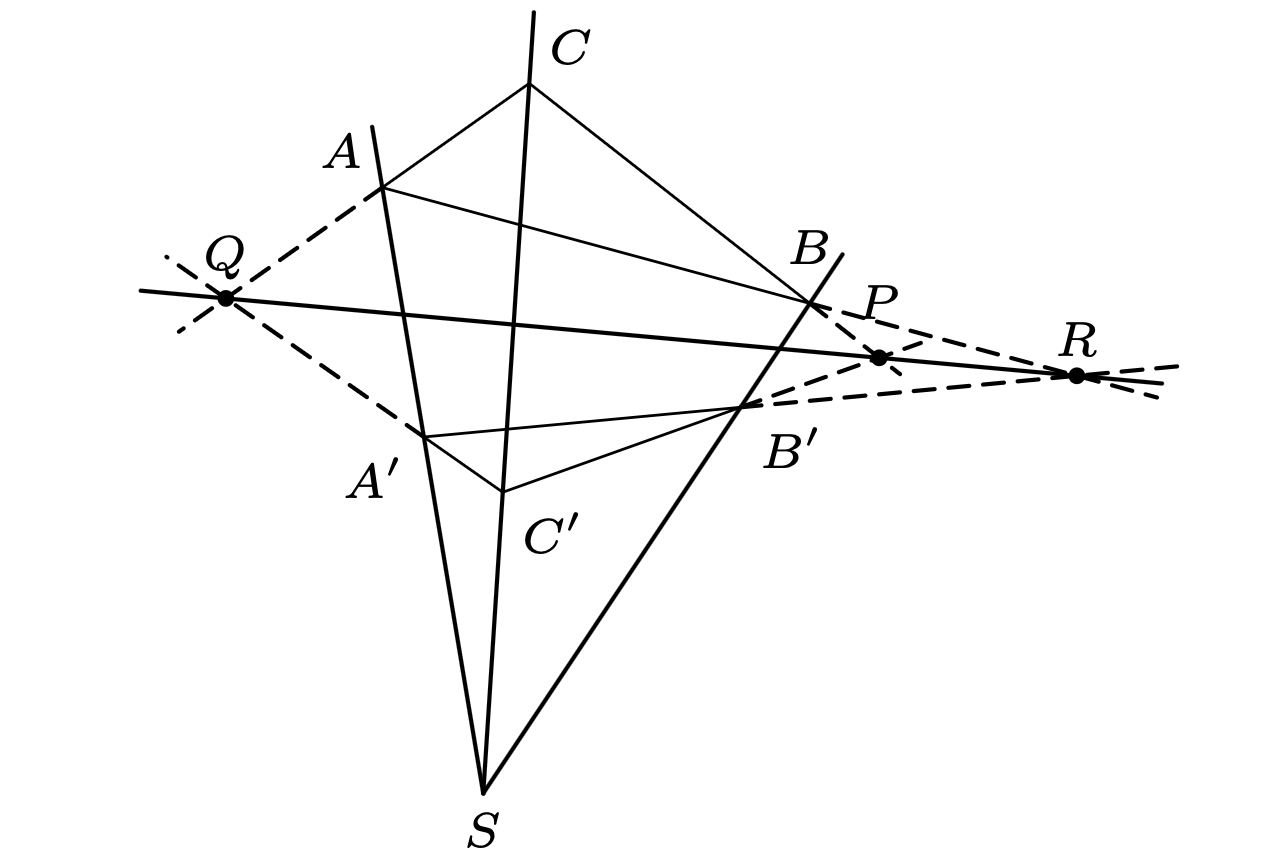Załóżmy, że proste \(AA',\) \(BB',\) \(CC'\) przecinają się w jednym punkcie
\(S.\) Dowód rozbijemy na dwa przypadki. Załóżmy najpierw, że trójkąty \(ABC\) i \(A'B'C'\) leżą w różnych płaszczyznach. Skoro \(CC'\) i \(BB'\) się przecinają, to są
zawarte w jednej płaszczyźnie. Oznacza to więc, że \(BC\) i \(B'C'\) się przecinają,
czyli punkt \(P\) istnieje. Leży on ponadto w płaszczyźnie \(\pi\) trójkąta \(ABC\)
(bo \(BC\) zawiera się w \(\pi\)) oraz w płaszczyźnie \(\pi'\) trójkąta \(A'B'C'\) (bo \(B'C'\) zawiera się w \(\pi'\)). Podobne rozumowanie dla punktów \(Q\) i \(R\) pokazuje, że punkty te
istnieją i leżą na \(\pi \cap \pi',\) czyli na prostej.
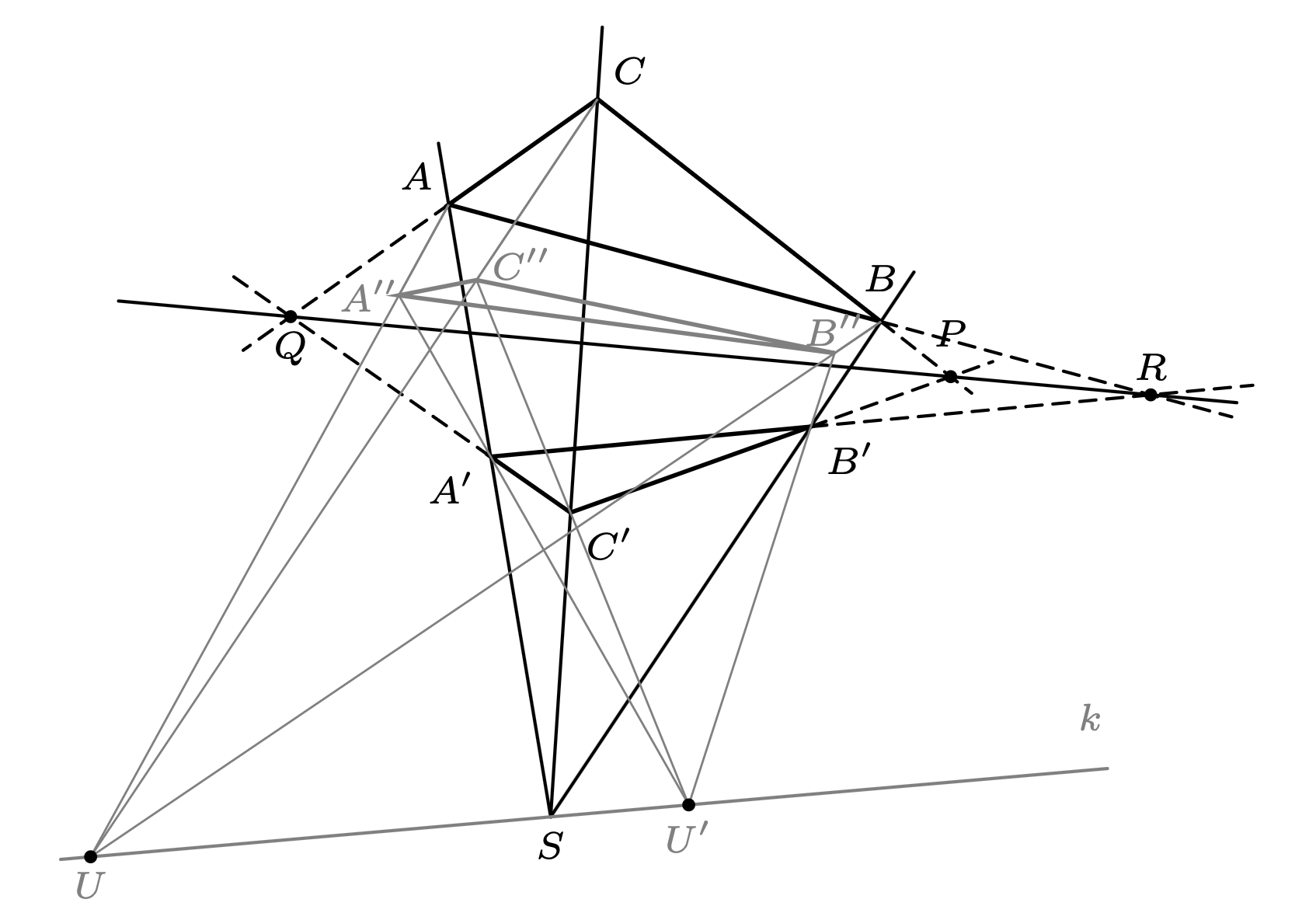
Rozważmy teraz trudniejszy przypadek, gdy trójkąty \(ABC\) i \(A'B'C'\) są zawarte w tej samej płaszczyźnie \(\pi\) (zazwyczaj w takiej postaci podawane jest to twierdzenie). Istnienie punktów \(P,\) \(Q,\) \(R\) mamy wówczas za darmo, lecz to współliniowość jest główną trudnością. Niech \(k\) będzie dowolną prostą przez \(S,\) wychodzącą poza \(\pi.\) Niech ponadto \(U\) i \(U'\) to dowolne (różne) punkty na \(k.\) Proste \(AA'\) i \(UU'\) przecinają się (w \(S\)), więc są one zawarte w jednej płaszczyźnie. Wynika stąd, że proste \(AU\) i \(A'U'\) przecinają się w pewnym punkcie \(A''\) leżącym poza \(\pi.\) Podobnie: niech \(B'' = BU \cap B'U'\) oraz \({C'' = CU \cap C'U'}.\) Niech \(\pi''\) będzie płaszczyzną zawierającą punkty \(A'',\) \(B'',\) \(C''\) (więc \(\pi''\neq\pi\)). Proste \(AA'',\) \(BB'',\) \(CC''\) przecinają się w \(U,\) więc z udowodnionego już przypadku punkty \({P_1 = BC \cap B''C''},\) \(Q_1 = CA \cap C''A'',\) \({R_1 = AB \cap A''B''}\) istnieją i są współliniowe. Podobnie: punkty \({P_2 = B'C' \cap B''C''},\) \(Q_2 = C'A' \cap C''A'',\) \({R_2 = A'B' \cap A''B''}\) istnieją i są współliniowe. Zauważmy finalnie, że skoro \(P_1\) i \(P_2\) są punktami na \(B''C''\) oraz na \(\pi,\) to \(P_1=P_2\) (prosta niezawarta w płaszczyźnie przecina ją dokładnie w jednym punkcie), czyli jest to również punkt \(P.\) Analogiczne rozumowanie dla \(Q\) i \(R\) kończy więc dowód wynikania w jedną stronę. Dowód w drugą stronę pozostawiamy Czytelnikowi jako ćwiczenie (wskazówka: wystarczy odwrócić powyższe rozumowanie).
Zademonstrowane przykłady rozwiązań trójwymiarowych w planimetrii są jedynie kilkoma ze znacznie szerszej klasy. Zachęcam więc Ciebie, Drogi Czytelniku, do poszukiwania tego typu sposobów myślenia w napotykanych problemach. Dla nienasyconych miłośników geometrii zostawiam jeszcze garść zadań (według mnie, o rosnącym poziomie trudności) do samodzielnego przemyślenia:
-
Czy istnieje taki pięciokąt wypukły \(A_1A_2A_3A_4A_5,\) że dla każdego \(i = 1,2,\dots ,5\) proste \(A_iA_{i+1}\) oraz \(A_{i+2}A_{i+4}\) nie są równoległe, przecinają się w punkcie \(B_i,\) a punkty \(B_1, B_2, \dots , B_5\) są współliniowe? (Przyjmujemy, że \(A_6 = A_1,\) \(A_7 = A_2\) itd.)
Wskazówka Warto zacząć rozwiązanie od znalezienia przykładu na płaszczyźnie rzutowej (pomijając wymóg braku równoległości z treści zadania). -
(Twierdzenie Johnsona) Przystające okręgi \(o_1,\) \(o_2,\) \(o_3\) przechodzą przez punkt \(S.\) Niech \(o_2 \cap o_3 = \{A,S\},\) \(o_3 \cap o_1 = \{B,S\}\) oraz \(o_1 \cap o_2 = \{C,S\}.\) Udowodnij, że okrąg opisany na trójkącie \(ABC\) przystaje do bazowych okręgów.
Wskazówka Między punktami z zadania narysuj 9 odcinków tej samej długości. Czy rysunek nie przypomina pewnej bryły? Jakiego punktu na nim brakuje? -
Czy istnieje w \(\mathbb{R}^2\) konfiguracja skończenie wielu okręgów o rozłącznych wnętrzach, w której każdy okrąg jest styczny do dokładnie pięciu innych?
Wskazówka Zacznij od znalezienia takiej konfiguracji okręgów rozmieszczonych na sferze. Jakiego przekształcenia można użyć, by przenieść ten układ na płaszczyznę?
A co, gdyby pójść dalej? Zachęcam do próby znalezienia takiego problemu trójwymiarowego, żeby jego rozwiązanie było dużo prostsze, patrząc z perspektywy wymiaru czwartego. Warto zainspirować się którymś (bądź kilkoma) z problemów przedstawionych w artykule.