Afiliacja: Instytut Matematyki Stosowanej i Mechaniki, Uniwersytet Warszawski
[…] i to jest główną naszą troską, byśmy niczego nie przyjmowali za prawdę, co najmniejszemu nawet podlega powątpiewaniu. – René Descartes
Albowiem zastąpienie możliwości logicznej pojęcia (mianowicie, że pojęcie nie zaprzecza samemu sobie) możliwością transcendentalną rzeczy (mianowicie, że jakiś przedmiot odpowiada pojęciu) może zwodzić i zadowalać tylko naiwnych. – Immanuel Kant
Naszym celem jest przedstawienie artykułu Georga Cantora z 1874 roku, będącego pierwszą publikacją z nowej dziedziny matematyki – teorii mnogości – w szerszym kontekście historycznym, a w szczególności, omówienie jego pięknego i mającego duży potencjał wyniku:

Georg Cantor (1845–1918)

Joseph Liouville (1809–1882)
Liczbami algebraicznymi nazywamy pierwiastki wielomianów o współczynnikach całkowitych. Liczby niealgebraiczne to liczby, które nie są algebraiczne. W tym artykule rozważamy tylko liczby rzeczywiste.
Mając dowolny ciąg liczb rzeczywistych \(S\) i dowolny przedział \([\alpha, \beta]\) na prostej rzeczywistej, można w \([\alpha, \beta]\) wyznaczyć liczbę \(\eta,\) która nie należy do \(S.\) Można zatem wyznaczyć nieskończenie wiele takich liczb \(\eta\) w \([\alpha, \beta].\)
Oryginalne sformułowanie było wyrażone w terminologii zrozumiałej przez współczesnych i zawierało ograniczenia dodatkowe, świadomie wprowadzone przez Cantora dla podkreślenia konstruktywności i przejrzystości rozważań.
Twierdzenie 1 . Jeśli mamy (przeliczalnie) nieskończony ciąg \(\omega_1, \omega_2,\ldots, \omega_\nu,\ldots\) różnych od siebie liczb rzeczywistych, które przebiegają według jakiejś reguły, to w każdym danym przedziale \([\alpha, \beta]\) można wyszczególnić liczbę \(\eta\) (a więc także nieskończenie wiele z nich), która nie występuje w tym ciągu (jako jego element).
Cantor użył powyższego twierdzenia w tym samym artykule do dowodu istnienia liczb niealgebraicznych (zob. margines)
oraz do sformułowania, jako wniosku, twierdzenia o niemożliwości ustawienia zbioru wszystkich liczb rzeczywistych w ciąg ponumerowany liczbami naturalnymi, czyli o nieprzeliczalności zbioru liczb rzeczywistych. Porządek logiczny argumentacji Cantora jest następujący.Zaproponował on sposób ustawienia liczb algebraicznych w ciąg, dowodząc tym samym ich przeliczalności. Następnie argumentuje, że jeśli za \(S\) weźmiemy ciąg wszystkich liczb algebraicznych, to powyższe twierdzenie dowodzi istnienia nieskończenie wielu liczb niealgebraicznych, inaczej przestępnych, w dowolnym przedziale na prostej liczbowej.
W końcu formułuje wniosek, że zbiór wszystkich liczb rzeczywistych jest nieprzeliczalny – zakładając jego przeliczalność i biorąc za \(S\) ciąg zawierający wszystkie liczby rzeczywiste, otrzymujemy sprzeczność.
Zauważmy, że z przeliczalności zbioru liczb algebraicznych i nieprzeliczalności zbioru liczb rzeczywistych wynika istnienie oraz nieprzeliczalność zbioru liczb przestępnych, ale ta odwrócona argumentacja daje niekonstruktywny dowód istnienia tych ostatnich i Cantor nie zamieścił jej w rozważanym artykule.
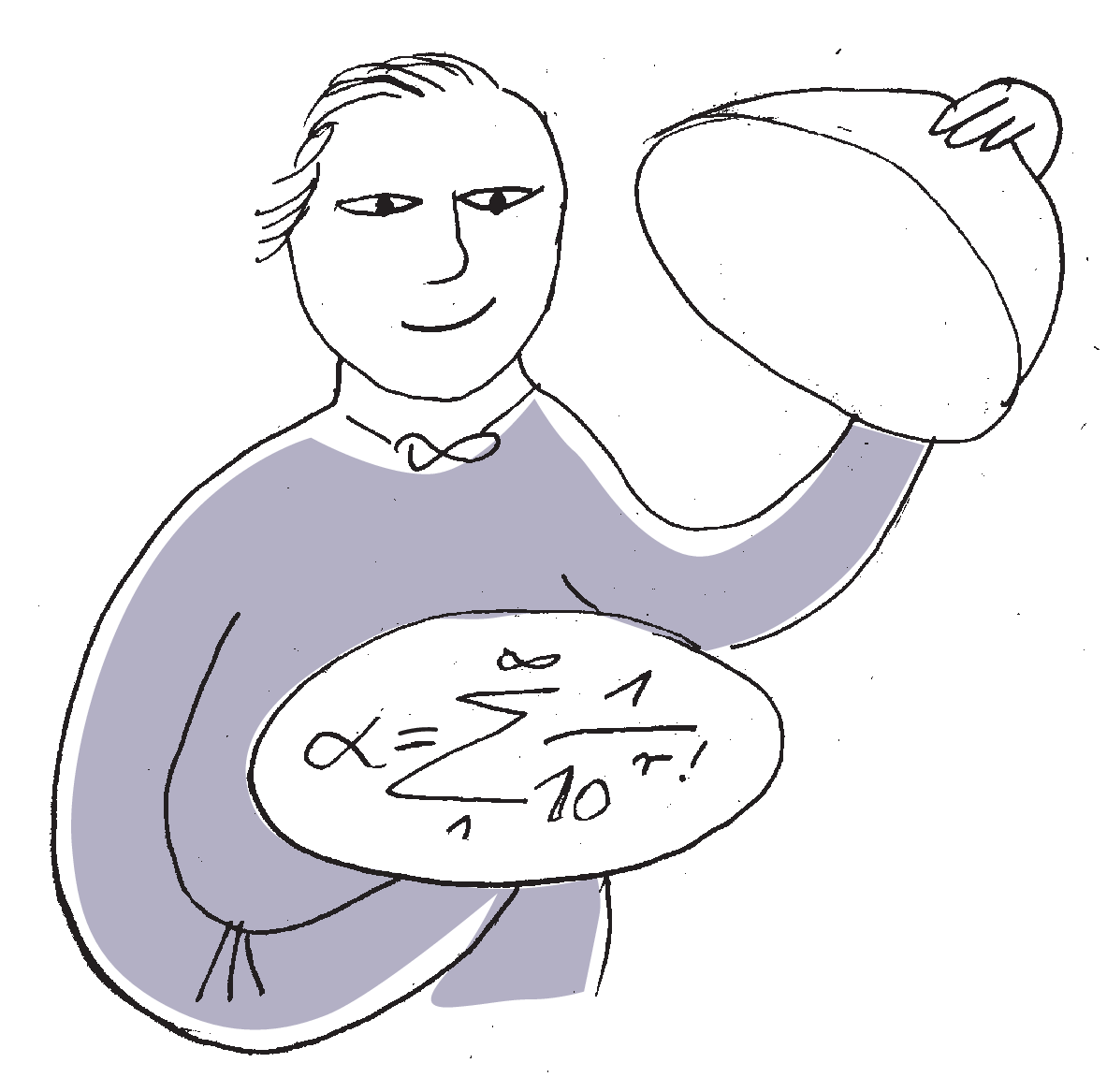
Pierwszą konkretną liczbę przestępną podał Joseph Liouville w 1851 roku, ale już w roku 1844 pokazał, jak można je konstruować. Wcześniej tylko domniemywano, że pewne liczby są liczbami przestępnymi. Liczba z 1851 to liczba \(\alpha\) dana wzorem: \[\begin{aligned} \label{alpha-def} \alpha=\sum_{r=1}^{\infty}\frac{1}{10^{r!}}= \frac{1}{10^{1!}}+\frac{1}{10^{2!}}+\frac{1}{10^{3!}}+\frac{1}{10^{4!}} + \ldots \end{aligned}\] Dowód Liouville’a przestępności liczby \(\alpha\) opierał się na jego własnym wyniku znanym dziś jako Twierdzenie Aproksymacyjne Liouville’a [Havil, 2012]:
Jeśli \(\alpha\) jest pierwiastkiem niewymiernym nieredukowalnego wielomianu \[\begin{aligned} \label{polyn} f(x) = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \ldots + a_0 \end{aligned}\] o współczynnikach całkowitych, to dla dowolnego \(\varepsilon>0\) istnieje tylko skończenie wiele liczb wymiernych \(p/q\) spełniających nierówność \[|\alpha-p/q| < 1/q^{n+\varepsilon}.\] Liouville pokazał, że w przypadku liczby \(\alpha\) określonej w (3) powyższa nierówność zachodzi dla nieskończonego ciągu liczb wymiernych \(p_k/q_k,\) gdzie \[p_k=10^{k!} \left( \frac{1}{10^{1!}}+\frac{1}{10^{2!}}+\frac{1}{10^{3!}}+\ldots+\frac{1}{10^{k!}} \right), \ \ \ q_k=10^{k!}.\] Istotnie, porównując \(|\alpha-p_k/q_k|\) z szeregiem geometrycznym, mamy \[\frac{1}{10^{(k+1)!}}+\frac{1}{10^{(k+2)!}} +\ldots < \frac{1}{10^{(k+1)!}} \left( 1+\frac{1}{10}+\frac{1}{10^2} +\ldots \right) = \frac{\frac{10}{9}}{q_k^{k+1}}< \frac{1}{q_k^{n+\varepsilon}}\] dla wszystkich \(k\) spełniających \(q_k^{k+1-n-\varepsilon} > 10/9,\) zatem \(\alpha\) nie może być liczbą niewymierną algebraiczną. Z racji swej konstrukcji – jej rozwinięcie dziesiętne jest nieskończone i nieokresowe – nie jest też liczbą wymierną, a więc jest liczbą przestępną.
Dowód Cantora istnienia liczb przestępnych, jak wspomnieliśmy powyżej, oparty jest na Twierdzeniu 1, które jego autor dowodzi następująco. Niech \(S\) będzie ciągiem \(\omega_1,\omega_2, \omega_3, \ldots\) liczb rzeczywistych postulowanym w twierdzeniu. Z tego ciągu wybieramy pierwsze dwie liczby należące do wnętrza przedziału \([\alpha, \beta],\) oznaczamy mniejszą z nich przez \(\alpha_1,\) a większą przez \(\beta_1.\) Powtarzamy tę procedurę dla przedziału \([\alpha_1,\beta_1],\) znajdując w jego wnętrzu liczby \(\alpha_2\) i \(\beta_2,\) należące do ciągu \(S.\) Powtarzamy tę procedurę dla przedziału \([\alpha_2,\beta_2]\) i tak dalej. Otrzymamy w ten sposób pewien ciąg przedziałów zstępujących.
Jeśli ciąg ten jest skończony, tzn. \([\alpha_1,\beta_1],\) \([\alpha_2,\beta_2],\) …, \([\alpha_N,\beta_N]\) dla pewnej liczby naturalnej \(N,\) to we wnętrzu ostatniego przedziału znajduje się co najwyżej jeden element \(\omega\) ciągu \(S.\) Wtedy dowolna różna od \(\omega\) liczba we wnętrzu tego przedziału nie należy do ciągu \(S.\)
Jeśli natomiast ciąg przedziałów jest nieskończony, to zachodzi zbieżność: \[\lim_{n\to\infty}\alpha_n = \alpha_\infty \le \beta_\infty = \lim_{n\to\infty}\beta_n.\] Albo wspólna część tych przedziałów jest niezdegenerowanym przedziałem \([\alpha_\infty, \beta_\infty],\) i wówczas dowolna liczba \(\eta\) we wnętrzu przedziału nie należy do ciągu \(S,\) albo \(\alpha_\infty = \beta_\infty =: \eta.\) Zauważmy, że \(\eta\) nie może należeć do ciągu \(S,\) gdyż dla każdego \(n,\) \(\omega_n\) nie należy do \([\alpha_{n+1},\beta_{n+1}].\) Twierdzenie jest udowodnione.
Spełniający pełne wymagania konstruktywistów dowód twierdzenia Cantora można znaleźć w [Bishop, 1985].
Cantor obawiał się, że redakcja znakomitego czasopisma, w którym publikowali wcześniej Niels Abel i Carl Friedrich Gauss, mogłaby odrzucić jego artykuł ze względu na użyte w nim nowatorskie argumenty, w tym zanegować jego przełomowy wynik o niemożliwości ustawienia zbioru wszystkich liczb rzeczywistych w ciąg ponumerowany liczbami naturalnymi. Użył zatem pewnego podstępu. Już sam tytuł artykułu O własności zbioru wszystkich rzeczywistych liczb algebraicznych miał uspokoić, czy może zmylić, redaktorów, a szczególnie nieprzejednanego konstruktywistę Leopolda Kroneckera (1823–1891), sugerując, że główny wynik artykułu dotyczy możliwości ustawienia w ciąg liczb algebraicznych. Artykuł został szybko opublikowany.
Należy w tym miejscu oddać sprawiedliwość Kroneckerowi, jednemu z największych matematyków XIX wieku, przedstawianemu czasem niesłusznie jako wroga samego Cantora. Kroneckerowi zależało na tym, aby matematyka była oparta na solidnych podstawach i, będąc redaktorem, blokował artykuły zawierające enigmatyczne argumenty, w szczególności te oparte na nieostrych definicjach rozważanych obiektów i ryzykownej logice.
Konstrukcja matematyczna (a) i pewnik wyboru (b):
(a) Niech \(A\) będzie zbiorem niepustych, parami rozłącznych przedziałów \(\{(n,n+1): n=1,2,3, \ldots\}\) na prostej liczbowej. Określamy zbiór \(S\) jako zbiór liczb \(\{n+1/2: n=1,2,3, \ldots\}\) będących środkami tych przedziałów.
(b) Dla każdej rodziny \(A\) niepustych zbiorów parami rozłącznych istnieje zbiór \(S,\) do którego należy dokładnie jeden element z każdego ze zbiorów należących do rodziny \(A.\)
Konstrukcja w punkcie (a) jest oczywista dla każdego, natomiast przyjęcie stwierdzenia w punkcie (b) za prawdziwe jest aktem wiary w przypadku nieskończonej, w szczególności nieprzeliczalnej, liczby zbiorów.
Uważał, że dopuszczenie do argumentacji matematycznej niekonstruktywnych i nieintuicyjnych uzasadnień nie powinno mieć miejsca. W końcu jednak do tego doszło, Kronecker przegrał, przeważyły nowe nurty i… pojawiły się paradoksy, a w ślad za nimi poważny kryzys w matematyce, która utraciła spójność i pewność [Kline, 1982]. Kronecker byłby przerażony, gdyby się dowiedział, że np. stwierdzenie (b), zamieszczone na marginesie, będzie w niedalekiej przyszłości zaliczone do aksjomatów tak zwanych podstaw matematyki. Obecny trend ku myśleniu algorytmicznemu, będący konsekwencją łatwo dostępnych efektywnych komputerowych technik obliczeniowych, można uznać za swoistą rehabilitację na długo odsuniętego w cień Kroneckera.
Następny artykuł Cantora, z roku 1878, i dalsze prace zawierają już coraz odważniejsze rozważania dotyczące operacji na zbiorach nieskończonych, wywołując głosy krytyczne. Zarzuty dotyczyły między innymi samej materii dowolnych zbiorów nieskończonych i niekonstruktywności dowodów. Zarzut niekonstruktywności dowodu istnienia liczb przestępnych został też sformułowany pod adresem jego pierwszego artykułu, tego z 1874 roku, co było oczywistym nieporozumieniem, wynikającym z tego, że, jak to wyraził A. Kanamori: „w opisach twórczości Cantora w większości przypadków odwrócono kolejność wnioskowania o istnieniu liczb przestępnych, ustalając najpierw nieprzeliczalność zbioru liczb rzeczywistych, a dopiero potem wyciągając wniosek o istnieniu [liczb przestępnych] z przeliczalności zbioru liczb algebraicznych”. [Wikipedia]
Choć pojawiały się też głosy broniące konstruktywności dowodu istnienia liczb niealgebraicznych w artykule [Cantor, 1874], np. w 1930 roku Abraham Fraenkel stwierdził, że metoda opisana w tym artykule jest „metodą, która – nawiasem mówiąc, wbrew powszechnej interpretacji – jest zasadniczo konstruktywna, a nie tylko egzystencjalna”, to nieporozumienie co do charakteru tego dowodu trwało nadal. Jeszcze w 1968 roku Mark Kac i Stanisław M. Ulam [Kac, 1968] pisali:
„Kontrast między metodami Liouville’a i Cantora jest uderzający, a metody te stanowią doskonałą ilustrację dwóch całkowicie odmiennych podejść do udowadniania istnienia obiektów matematycznych. Liouville jest czysto konstrukcyjny, Cantor jest czysto egzystencjalny”.
Zobaczmy najpierw, jak ten „czysto egzystencjalny” dowód Cantora wygląda na prostym przykładzie.
Przykład. Niech \([\alpha, \beta]=[1,2]\) oraz niech \[\begin{aligned} \label{wymierne}\let\frac\tfrac S = \bigl\{ \frac{3}{2}, \frac{4}{3}, \frac{5}{3}, \frac{5}{4}, \frac{7}{4}, \frac{6}{5}, \frac{7}{5}, \frac{8}{5}, \frac{9}{5}, \frac{7}{6}, \frac{11}{6}, \frac{8}{7},\frac{9}{7},\frac{10}{7}, \frac{11}{7},\frac{12}{7},\frac{13}{7}, \ldots \bigr\} \end{aligned}\] będzie ciągiem wszystkich liczb wymiernych we wnętrzu tego przedziału, ustawionych według widocznej reguły.
Pierwszymi dwoma wyrazami ciągu \(S\) są \(\frac{3}{2}\) i \(\frac{4}{3}.\) Oznaczmy \(\alpha_1=\frac{4}{3},\) \(\beta_1=\frac{3}{2}.\) Pierwszymi dwoma wyrazami ciągu \(S\) należącymi do przedziału \([\alpha_1,\beta_1]\) są liczby \(\alpha_2=\frac{7}{5}\) i \(\beta_2=\frac{10}{7}.\) Pierwszymi dwoma wyrazami ciągu \(S\) należącymi do przedziału \([\alpha_2,\beta_2]\) są liczby \(\alpha_3=\frac{24}{17}\) i \(\beta_3=\frac{17}{12},\) definiujące przedział \([\alpha_3,\beta_3].\) Okazuje się, że gdy mamy liczby \(\alpha_1\) i \(\beta_1,\) następne wyrazy ciągu par \((\alpha_n,\beta_n)\): \((\frac{24}{17},\frac{17}{12}),\) \((\frac{41}{29},\frac{58}{41}),\) \((\frac{140}{99},\frac{99}{70}), \ldots,\) definiuje następujący prosty algorytm. Na początku, w przedziale \([\frac{4}{3},\frac{3}{2}]\) mamy wskazać dwie pierwsze liczby ciągu \(S\) należące do tego przedziału. Liczby te, zgodnie z ustawieniem elementów ciągu \(S,\) będą miały możliwie najmniejsze mianowniki. Liczbą o najmniejszym mianowniku w tym przedziale jest liczba \(\frac{7}{5}\) jako medianta liczb \(\frac{4}{3}\) i \(\frac{3}{2},\) czyli liczba \(\frac 43 < \frac{4+3}{3+2} < \frac 32.\) Jako drugą liczbę bierzemy \(\frac{10}{7},\) mediantę liczb \(\frac{7}{5}\) i \(\frac{3}{2},\) \(\frac{7}{5}< \frac{10}{7}=\frac{7+3}{5+2} < \frac{3}{2},\) kierując się tym, że \(5+2<3+5.\) Zatem: \(\frac{7}{5}=\alpha_2\) i \(\frac{10}{7}=\beta_2.\) W następnym kroku medianta \(\frac{17}{12}\) liczb \(\frac{7}{5}\) i \(\frac{10}{7}\) będzie liczbą \(\beta_3,\) i ta naprzemienność się utrzyma. Postępując dalej, otrzymujemy dwa ciągi, rosnący i malejący: \[\frac{4}{3} < {\bf \frac{7}{5}}<\frac{24}{17}< {\bf \frac{41}{29}}<\frac{140}{99} <{\bf \frac{239}{169}}<\ldots<\frac{338}{239}< {\bf \frac{99}{70}}<\frac{58}{41} <{\bf \frac{17}{12}} < \frac{10}{7}< {\bf \frac{3}{2}}.\]Uzasadnienie poprawności przedstawionego algorytmu Czytelnik odnajdzie w artykule o ciągach Fareya z \(\Delta^5_{10}\). Wytłuszczone liczby \({\bf \frac{3}{2}, \frac{7}{5}, \frac{17}{12},\frac{41}{29},\frac{99}{70}, \frac{239}{169}, \ldots}\) są kolejnymi reduktami rozwinięcia liczby \(\sqrt{2}\) w ułamek łańcuchowy [Łukaszewicz, 2025], co też wynika z powyższej konstrukcji. Widzimy zatem, że w naszym przypadku procedura Cantora zastosowana do ciągu (1) prowadzi do wykazania istnienia liczby niewymiernej \(\sqrt{2}.\)
Dla \(\frac{p_0}{q_0}=\frac{1}{1},\) \(\frac{p_1}{q_1}=\frac{3}{2}\) dalsze redukty ułamka łańcuchowego liczby \(\sqrt{2}\) dane są wzorem rekurencyjnym: \(\frac{p_{n+1}}{q_{n+1}}= \frac{2p_n+p_{n-1}}{2q_n+q_{n-1}}= \frac{(p_n+p_{n-1})+p_n}{(q_n+q_{n-1})+q_n},\) co oznacza, że medianta medianty i reduktu jest reduktem.
Jeśli za \(S\) weźmiemy odpowiednio ustawiony ciąg liczb algebraicznych, to analogiczna procedura doprowadzi do liczby przestępnej, którą można obliczyć z żądaną dokładnością \(n\) miejsc po przecinku, posługując się programem komputerowym, opisanym w [Gray, 1994]. Zilustrujmy ją pokrótce. Przyporządkujmy wielomianowi (2) stopnia \(n\) liczbę \(h=n+|a_0|+|a_1|+|a_2|+ \ldots +|a_n|\) i nazwijmy ją wysokością wielomianu. Uporządkowanie w ciąg wszystkich liczb algebraicznych zaproponowane przez Cantora polega na ustawieniu najpierw w ciąg wszystkich wielomianów według rosnącego \(h,\) znalezieniu wszystkich pierwiastków wielomianów dla każdego \(h\) i uporządkowaniu ich według wielkości w obrębie \(h,\) a następnie ustawieniu ich w ciąg kolejnymi grupami.
| Wysokość \(h\) | Stopień \(n\) | Wielomian | Pierwiastki |
|---|---|---|---|
| 2 | 1 | \(x\) | \(0\) |
| 3 | 1 | \(2x,\) \(x \pm 1\) | \(0,\) \(\pm 1\) |
| 2 | \(x^2\) | ||
| 4 | 1 | \(3x,\) \(2x \pm 1,\) \(x \pm 2\) | \(0,\) \(\pm \tfrac{1}{2}\) |
| 2 | \(2x^2,\) \(x^2 \pm 1,\) \(x^2 \pm x\) | \(\pm 1,\) \(\pm 2\) | |
| 3 | \(x^3\) | ||
| 5 | 1 | \(4x,\) \(3x \pm 1,\) | \(0,\) \(\pm \tfrac{1}{3},\) \(\pm \tfrac{1}{2},\) |
| \(2x \pm 2,\) \(x \pm 3\) | \(\pm 1,\) \(\pm 3,\) \(\pm \tfrac{1}{\sqrt{2}}\) | ||
| 2 | \(3x^2,\) \(2x^2 \pm 1,\) \(x^2 \pm 2,\) | \(\pm \sqrt{2},\) \(\pm 2,\) | |
| \(2x^2 \pm x,\) \(x^2 \pm 2x,\) | \(\frac{\pm 1 \pm \sqrt{5}}{2}\) | ||
| \(x^2 \pm x \pm 1\) | |||
| 3 | \(2x^3,\) \(x^3 \pm 1,\) | ||
| \(x^3 \pm x,\) \(x^3 \pm x^2\) | |||
| 4 | \(x^4\) |
Tabelka powyżej przedstawia wszystkie wielomiany do wysokości \(h=5\) wraz z ich pierwiastkami. Te ostatnie ustawiamy w ciąg (bez powtórzeń), \[\bigl\{0,-1,1,-2,-\tfrac{1}{2},\tfrac{1}{2},2,-3, \tfrac{-1-\sqrt{5}}{2},-\sqrt{2}, \ldots \bigr\}.\] Ograniczając się do przedziału \([\alpha,\beta]=[0,1],\) otrzymujemy ciąg \[S=\{\omega_1,\omega_2,\omega_3,\omega_4,\omega_5,\omega_6, \ldots \} = \bigl\{0,1,\tfrac{1}{2},\tfrac{1}{3}, \tfrac{-1+\sqrt{5}}{2},\tfrac{1}{\sqrt{2}}, \ldots \bigr\}\] będący podciągiem tego poprzedniego i zawierający wszystkie liczby algebraiczne w tym przedziale. Zbiór liczb algebraicznych zawiera zbiór liczb wymiernych jako swój podzbiór, jest zatem gęsty w zbiorze liczb rzeczywistych. Stąd procedura Cantora zastosowana do ciągu \(S\) wyznaczy dokładnie jedną liczbę przestępną: \(\eta = \lim_{n\to\infty}\alpha_n = \lim_{n\to\infty}\beta_n.\)
Moglibyśmy spytać, dla jakiej najmniejszej liczby \(n\) zachodzi \(|\beta_n-\alpha_n|<\frac{1}{10^6}.\) Innymi słowy, pytanie dotyczy przybliżenia liczby \(\eta\) z dokładnością do \(\frac{1}{10^6}.\) Program komputerowy oparty na metodzie Cantora z 1874 roku, opisany w [Gray, 1994], wymaga asymptotycznie co najmniej \(O(2^{n^{1/3}})\) kroków, aby wyznaczyć \(n\) dokładnych cyfr, zatem jest mało efektywny. Przybliżenie liczby \(\eta\) z dokładnością do sześciu miejsc po przecinku wymaga przebiegnięcia ponad miliona liczb \(\omega_n,\) mamy \(\alpha_7 = \omega_{1406370} = 0{,}57341146 \ldots\) oraz \({\beta_7 = \omega_{1057887} = 0{,}57341183 \ldots}\)
W artykule [Gray, 1994] opisana jest też alternatywna metoda, gdzie wystarczy tylko \(O(n^2\log^2n\log\log n)\) kroków, co jest liczbą do przyjęcia w praktyce obliczeniowej.
Bibliografia
[Bishop, 1985] E. Bishop, D. Bridges, Constructive Analysis, Springer, 1985.
[Cantor, 1874] G. Cantor, Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen, [O własności zbioru wszystkich rzeczywistych liczb algebraicznych], J. Reine Angew. Math. 77 (1874), 258–262.
[Gray, 1994] R. Gray, Georg Cantor and Transcendental Numbers, The American Mathematical Monthly, 1994, Vol. 101(9), 819–832.
[Havil, 2012] J. Havil, The Irrationals, Princeton University Press, 2012.
[Kac, 1968] M. Kac, S. M. Ulam, Mathematics and Logic, New York, 1968.
[Kline, 1982] M. Kline, Mathematics. The Loss of Certainty, OUP, 1982.
[Łukaszewicz, 2025] G. Łukaszewicz, Geometria liczb, algorytmy Herona i Euklidesa i ułamki łańcuchowe, Delta 10/2025.
[Wikipedia] Cantor’s first set theory article,
en.wikipedia.org/wiki/Cantor’s_first_set_theory_article(dostęp: 04.08.2025).