W \(\Delta_{25}^{6}\) przedstawiliśmy sprytny, wizualny dowód tożsamości zwanej twierdzeniem Nikomacha. Dla naturalnych \(n\geq 1\) mamy \[1^3+2^3+3^3+\dots +n^3=(1+2+3+\dots +n)^2.\] Tym razem przedstawimy zupełnie inny dowód, którym uczcimy obchodzony 15 listopada Międzynarodowy Dzień Tabliczki Mnożenia.
O nieoczywistym zastosowaniu tabliczki mnożenia pisaliśmy również w \(\Delta^7_{25}\).
Dla wygody przyjmijmy oznaczenie \(n\)-tej liczby trójkątnej \(T(n)=1+2+3+\dots +n.\) Zauważmy także, że prawdziwa jest równość \[1+2+3+\dots +(n-1)+n+(n-1)+(n-2)+\dots +1=n^2.\] Istotnie, łatwo jest naszkicować argument indukcyjny: dla \(n=1\) jest to oczywiście prawda (\(1=1^2\)), przechodząc zaś z \(n\) do \(n+1,\) dopisujemy składniki \((n+1)+n\) po lewej stronie, gdy prawa wzrasta o \((n+1)^2-n^2=2n+1.\) Zatem różnica stron nie zmienia się, a wzór jest słuszny dla wszystkich \(n.\)
Czytelnik Obdarzony Niezwykłą Pamięcią przypomina sobie, że we wspomnianym artykule Trójkąty, kwadraty, sześciany ta pomocnicza tożsamość została uzasadniona geometrycznie.
Dla dowodu głównej tożsamości zastosujemy technikę podwójnego zliczania, dwukrotnie wyznaczając sumę liczb w kwadratowym narożu \(n\times n\) tabliczki mnożenia.
Zliczanie kolumnami. Najpierw obliczymy sumę liczb w każdej z kolumn, a następnie dodamy tak otrzymane sumy.
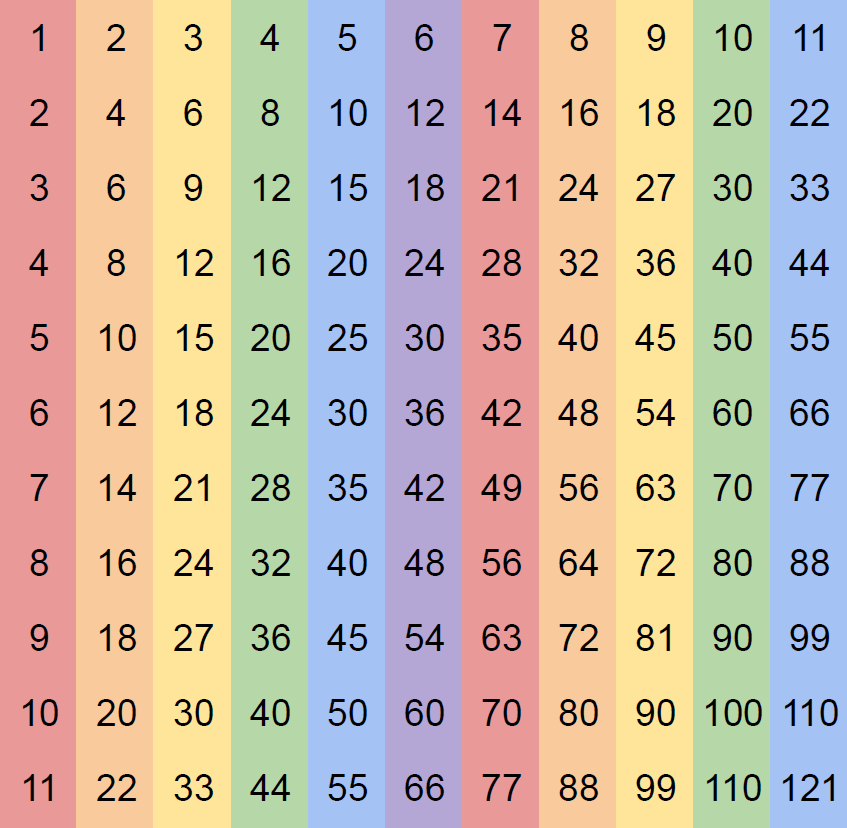
Suma liczb w \(k\)-tej kolumnie naszego naroża wynosi, licząc od góry, \[1k+2k+3k+\dots +nk=(1+2+3+\dots +n)\cdot k=kT(n).\] Suma liczb w całym narożu \(n \times n\) jest więc równa \[\begin{gathered} 1\cdot T(n)+2\cdot T(n)+3\cdot T(n)+\dots +n\cdot T(n)\\ =(1+2+3+\dots +n)\cdot T(n)=T(n)^2. \end{gathered}\] Jest to prawa strona głównej tożsamości.
Zliczanie warstwami. Podzielimy badane naroże na warstwy następująco: pierwsza warstwa zawiera tylko samo narożne pole; druga – pozostałe trzy pola zawarte w narożu \(2\times 2\); trzecia – pozostałych 5 pól w narożu \(3 \times 3\) i tak dalej: \(k\)-ta warstwa zawiera te pola naroża \(k\times k,\) które nie zawierają się w narożu \((k-1)\times(k-1).\) Jasne jest, że początkowe \(n\) warstw doskonale pokrywa całe naroże \(n\times n.\)
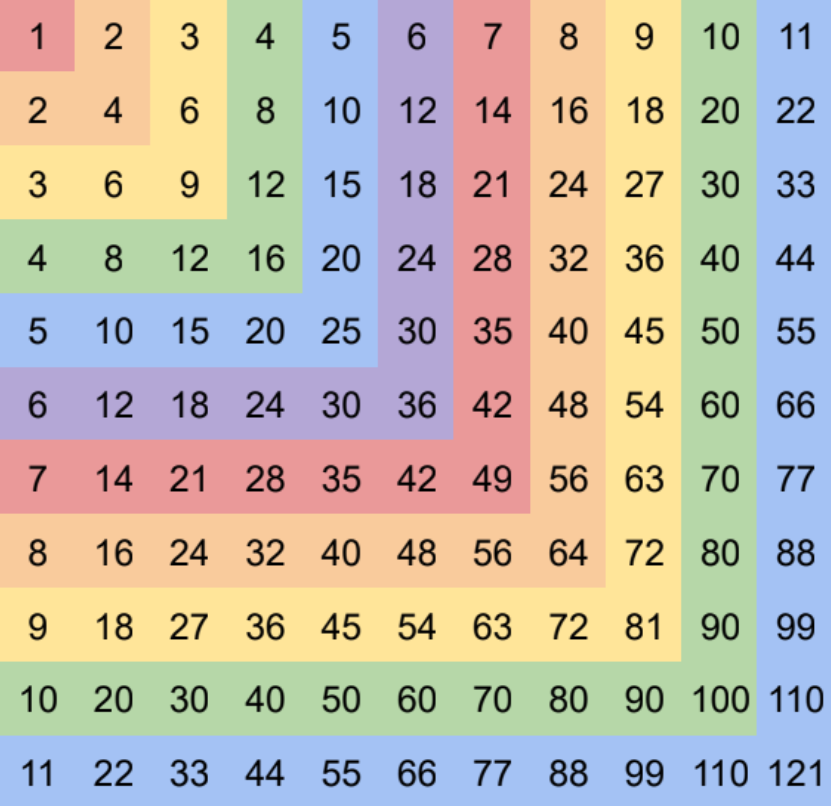
Obliczmy sumę liczb zawartych w \(k\)-tej warstwie. Wynosi ona \[\begin{gathered} 1k+2k+3k+\dots +(k-1)k+k^2+(k-1)k+\dots\\[-1pt]{} +3k+2k+1k\\[-1pt] \begin{aligned} & =(1+2+3+\dots +(k-1)+k+(k-1)+\dots +3+2+1)\cdot k \\[-1pt]&=k^2\cdot k=k^3, \end{aligned} \end{gathered}\] zgodnie z równością wykazaną we wstępie. Suma wszystkich liczb w narożu \(n\times n,\) pogrupowanych w kolejne warstwy, wynosi więc \(1^3+2^3+3^3+\dots +n^3.\) Ponieważ jest to lewa strona głównej tożsamości, jej dowód możemy uznać za zakończony.
Dowód ten ma kilka zalet; jedną z nich, która jak dotąd się nam nie ukazała, jest możliwość zademonstrowania go geometrycznie. Poniższa ilustracja pozwala zastąpić uprzednie zliczanie kolumnami prostym obliczeniem pola kwadratu.
Kolekcjonerzy dowodów mogą zajrzeć również do Małej Delty w \(\Delta^{10}_{94}\), gdzie Jarosław Górnicki przedstawia diagram jeszcze innego argumentu geometrycznego.

Dla Czytelnika Pragnącego Działać zostawiamy jeszcze jedno wyzwanie: Jaką tożsamość uzyskamy, stosując analogiczną technikę dla tabliczki mnożenia o wymiarach \(n\times 2n\)?