Afiliacja: Wydział Matematyki i Informatyki UJ
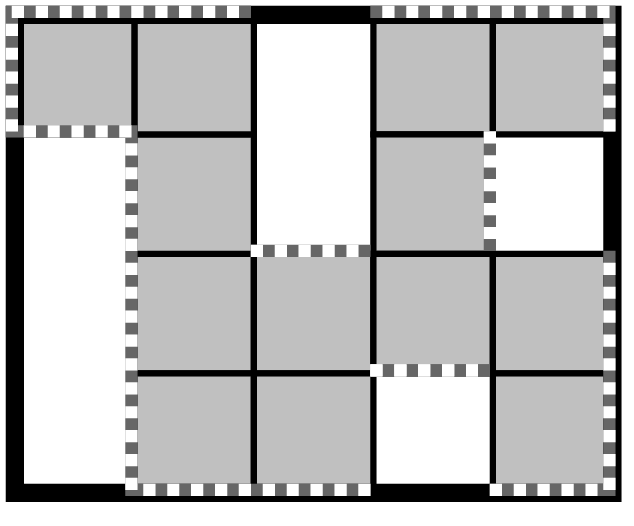
Poukładajmy jednostkowe kwadraty na płaszczyźnie. Jeden kwadrat oczywiście nie pozwala na żadną mnogość konfiguracji, a jego obwód wynosi 4 jednostki. Dwa też nie dają dużej swobody, jeśli chcemy, aby przylegały do siebie bokami. Przy takim założeniu można ułożyć tylko kostkę domina, o obwodzie 6. Począwszy od trzech kwadratów, pojawia się jakaś dowolność. Możliwości są jednak tylko dwie i obie dają taki sam obwód powstałego wielokąta. Cztery kwadraty można zestawić na aż 5 sposobów, w tym jeden o obwodzie 8 – takim samym, jak osiągany przez 3 kafelki. Jednak obwód obszaru pięciopolowego już nie może wynosić zaledwie 8 jednostek. Czytelnik może spróbować wyznaczyć kilka kolejnych wartości minimalnego obwodu figury ułożonej z \(n\) kwadratów (czyli tytułowego poliomina).
Małe układy kwadratowych kafelków (poliomina) i ich prostokąty ograniczające
W tym artykule przedstawimy pełny dowód jawnego wzoru na minimalny obwód. Wydaje się on całkiem ciekawy, ze względu na różnorodność kolejnych etapów, choć wszystkie są elementarne.
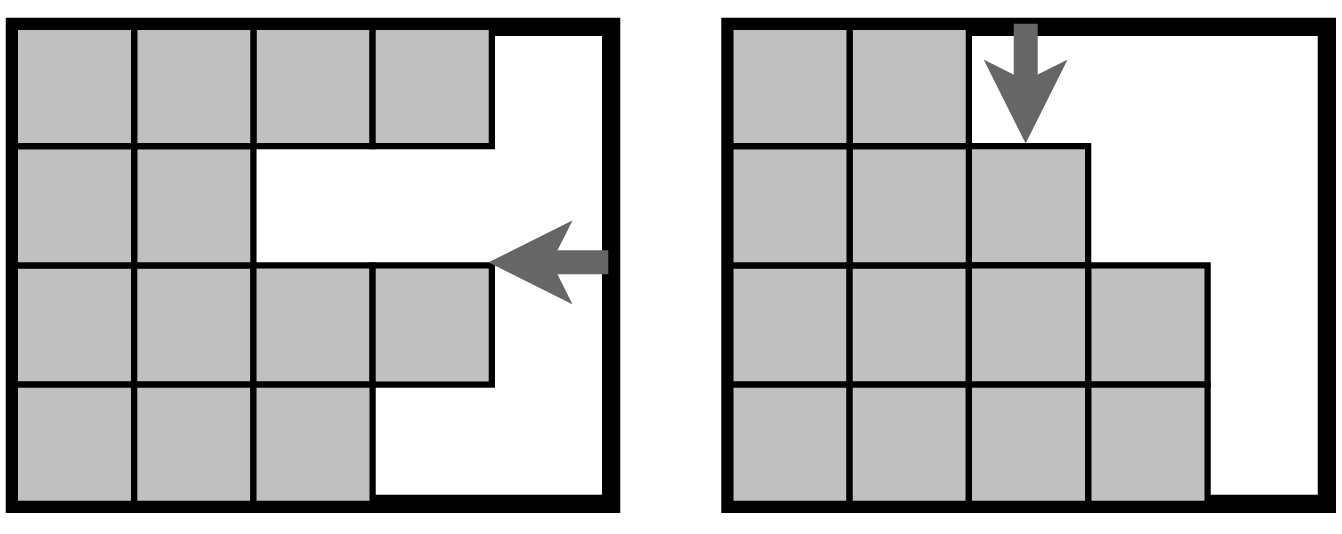
Możemy od razu przyjąć, że konfiguracje kafelków nie składają się z oddzielonych części; zsuwając ewentualne „wyspy”, możemy zmniejszyć łączny obwód, ponieważ miejsce styku przestanie się doliczać do obwodu. Zauważmy teraz, że na każdym układzie kwadratów można opisać dokładnie jeden minimalny prostokąt. Dowolny wiersz i dowolna kolumna tego prostokąta są przecinane przez co najmniej dwie krawędzie zewnętrzne ułożonej figury – tę przed pierwszym i tę za ostatnim polem leżącym w rozważanym wierszu. Możemy przypisać te krawędzie jednoznacznie do jednostkowych krawędzi tworzących obwód prostokąta – tych, które wyznaczają krańce rozważanego wiersza/kolumny. W ten sposób wykazaliśmy, że obwód prostokąta ograniczającego jest nie większy niż obwód układu kwadratowych kafelków.
Prostokąt ograniczający poliomino, na którego obwodzie zaznaczono krawędzie przypisane do obwodu prostokąta
Zauważmy teraz, że kafelki z danego wiersza możemy zsunąć na jedną (np. lewą) stronę, tak aby tworzyły jeden prostokąt (wysokości 1). Postępując tak z każdym wierszem, zapewnimy, że żaden z nich nie zawiera więcej niż dwóch krawędzi. Potem podobnego zsunięcia możemy dokonać w każdej z kolumn. Czy to nie „popsuje” nam żadnego wiersza? Nie, ponieważ po zsunięciu wierszy liczba kafelków w kolejnych kolumnach może się tylko zmniejszać – zatem po zsunięciu kolumn otrzymamy nierosnące „wieże”. Należy zauważyć, że podczas tego całego zsuwania prostokąt ograniczający mógł się pomniejszyć, ale to nie przeszkadza – wszak szukamy minimalnego obwodu. Zatem zachowując (lub wręcz zmniejszając) prostokąt ograniczający, byliśmy w stanie ułożyć wszystkie pola tak, że każdy wiersz i kolumna zawierają dokładnie dwie krawędzie, czyli obwód figury jest teraz równy obwodowi prostokąta ograniczającego!
Otrzymany efekt – spójność kolumn i wierszy – jest nazywany wypukłością poliomina
Pytanie zatem sprowadza się do tego, jaki najmniejszy obwód może mieć prostokąt o polu co najmniej \(n\)? Aby to rozstrzygnąć, pokażemy najpierw, że możemy ograniczyć uwagę do pewnego szczególnego typu prostokątów.
Nie trzeba chyba tłumaczyć obserwacji, że obwód prostokąta o całkowitych długościach boków jest liczbą parzystą.
\(\lfloor x \rfloor\) (podłoga z \(x\)) to największa liczba całkowita nie większa od \(x,\) natomiast \(\lceil x \rceil\) (sufit z \(x\)) to najmniejsza liczba całkowita nie mniejsza od \(x.\) Dla każdej liczby rzeczywistej \(x\) zachodzą nierówności \(x-1 < \lfloor x \rfloor \leq x \leq \lceil x \rceil < x+1.\)
Rozważmy dwa prostokąty, \(a\!\times\!b\) i \(c\!\times\!d,\) o jednakowym obwodzie. Zachodzi wtedy \((a+b)^2=(c+d)^2,\) czyli \(2(cd-ab) = a^2+b^2-c^2-d^2.\) Mając tę zależność, otrzymujemy kolejną: \[\begin{aligned} \underbrace{(a-b)^2 - (c-d)^2}_{\text{różnice długości boków}} & = a^2+b^2 -c^2-d^2 -2ab + 2cd \\&= 4 (\underbrace{cd - ab}_{\text{pola}}), \end{aligned}\] która oznacza, że prostokąt o mniejszej różnicy długości boków ma większe pole! Gdybyśmy mieli ustalony, całkowity obwód \(2k,\) to byłoby wiadomo, że aby zmaksymalizować pole prostokąta o takim obwodzie, należy znaleźć dwie liczby całkowite \(a,b\) spełniające \(a+b=k\) oraz minimalizujące różnicę \(|a-b|.\) Dla parzystego \(k\) odpowiedź to oczywiście \(a=b=k/2\) (nie sposób o mniejszą różnicę), a przypadek nieparzysty wymaga: \(a=\frac{k-1}2 =\lfloor k/2\rfloor,\) \(b=\frac{k+1}2 =\lceil k/2 \rceil\) (równość jest niemożliwa, wobec nieparzystości, więc różnica \(b-a=1\) jest optymalna). Tak określone prostokąty będziemy nazywać wypchanymi. Zauważmy, że jeśli \(n\) komórek można umieścić w prostokącie ograniczającym o obwodzie \(2k,\) to można je umieścić w wypchanym prostokącie o takim samym obwodzie. Teraz musimy tylko wyznaczyć najmniejsze \(k,\) dla którego wypchany prostokąt o obwodzie \(2k\) ma pole co najmniej \(n.\)
Prostokąt ograniczający figury realizującej minimalny obwód dla danego pola nie musi być wypchany. Ważne, że istnieje wśród nich (figur minimalizujących…) choć jedna o tej własności.
Niech \(k\) będzie największą liczbą całkowitą spełniającą \(k^2<n.\) Wtedy albo \(n\) kafelków mieści się w prostokącie \(k\!\times\!(k+1),\) albo dopiero w kwadracie \((k+1)\!\times\!(k+1).\) Pierwszy przypadek oznacza, że \(k^2 < n \leq k^2+k,\) co po pomnożeniu przez 4 daje \(4k^2 < 4n \leq 4k^2+4k.\) Jeśli z prawej strony dodamy 1, to nierówność będzie zachowana, a zyskamy możliwość zwinięcia do kwadratu: \({(2k)^2 < 4n \leq (2k+1)^2},\) czyli \({2k <\sqrt{4n} \leq 2k+1}.\) To oznacza ni mniej, ni więcej, tylko \({\lceil2\sqrt{n}\rceil = 2k+1}.\) Drugi przypadek jest analogiczny. Wiedząc, że \({k^2+k < n \leq (k+1)^2},\) ponownie mnożymy przez \(4\) i otrzymujemy, że \({(2k+1)^2 \leq 4n \leq (2k+2)^2}.\) Dodając 1 do \(4k^2+4k,\) pozornie straciliśmy silną nierówność, ale zauważmy, że \((2k+1)^2\) jest liczbą nieparzystą, czyli równość jednak nie może wystąpić. Po spierwiastkowaniu otrzymujemy \(\lceil2\sqrt{n}\rceil = 2k+2.\) W obu przypadkach sufit z podwojonego pierwiastka okazuje się połową obwodu odpowiedniego wypchanego prostokąta, czyli ostatecznie minimalny obwód dla \(n\) kwadratowych kafelków wynosi \(2 \lceil2\sqrt{n}\rceil.\)
Na koniec jeszcze krótka uwaga: jak ten wzór można szybko wyprowadzić metodą „na chłopski rozum”. Można odgadnąć (formalny dowód mamy zresztą za sobą), że dla \(n\) będących kwadratami wartość minimalnego obwodu wynosi \(4\sqrt{n}.\) Pozostaje ustalić, jak zaokrąglamy powyższą liczbę, gdy nie jest całkowita. Obwód musi być parzysty, ponadto przyjmijmy, że zaokrąglamy w górę. Takie zaokrąglanie (do nie mniejszej liczby parzystej) ma postać \(2\lceil x/2\rceil\) (proszę sprawdzić), co po podstawieniu \(x=4\sqrt{n}\) daje „nasz wzór”.
Jako przedsmak przyszłej odsłony przygody z obwodami spróbujmy teraz poukładać kafelki w kształcie równobocznych trójkątów. Zabawa nimi jest nieco trudniejsza, gdyż brakuje tu tak wspaniałego sprzymierzeńca jak papier w kratkę.
Istnieje papier w „trójkątną kratkę”, ale chyba nie każdy ma go w domu.
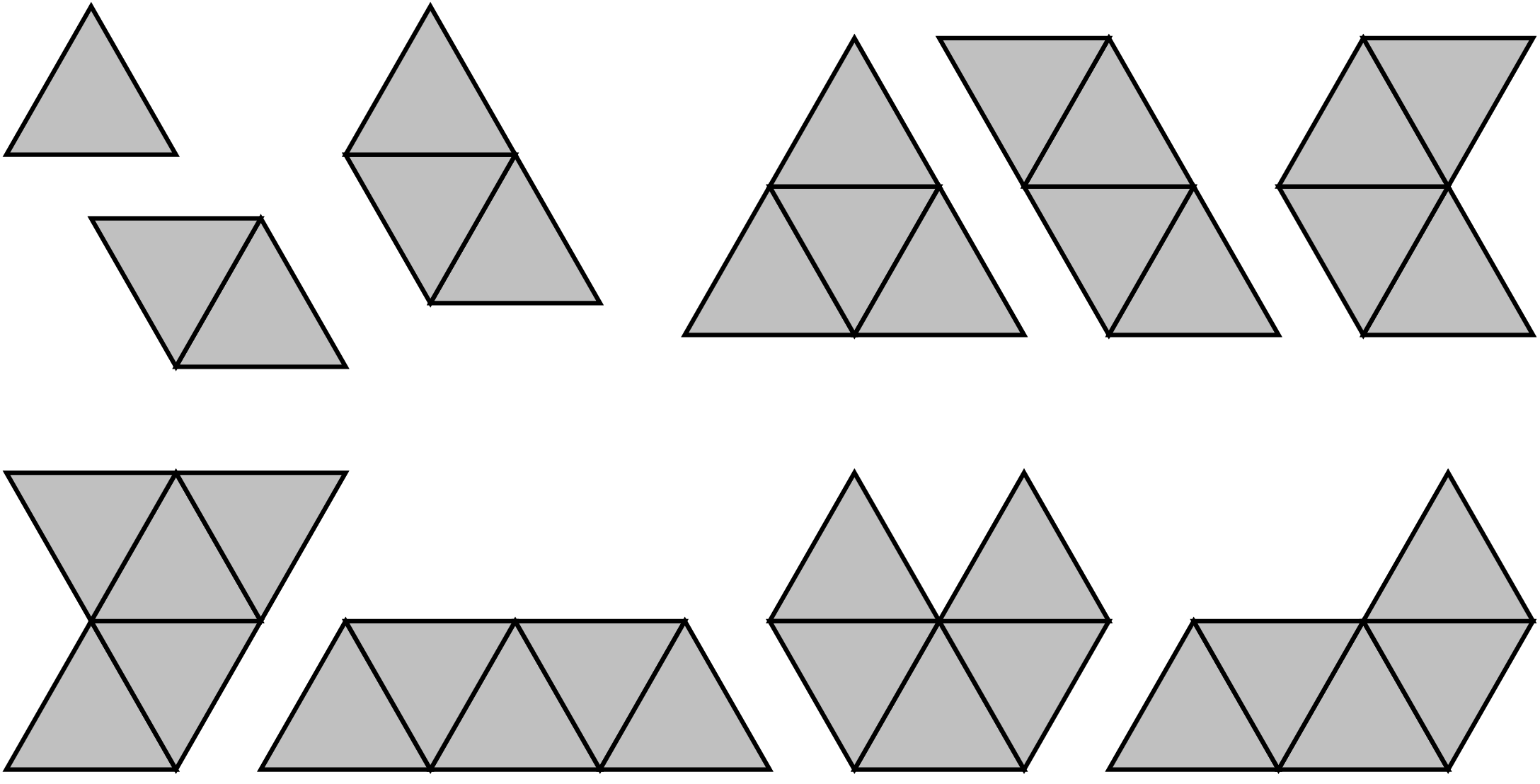
Tym razem jakakolwiek różnorodność pojawia się dopiero przy czterech polach, choć wszystkie trzy przypadki mają ten sam obwód (6). Dla pięciu kafelków również każda konfiguracja daje taki sam obwód (7). Do tego momentu otrzymujemy bardzo przyjemny postęp arytmetyczny, ale sześć trójkątów równobocznych pozwala nam zbudować sześciokąt foremny, którego obwód wynosi 6. Okazuje się, że funkcja minimalnego obwodu dla kafelków trójkątnych nie jest nawet monotoniczna!
Kształty ułożone z 1–5 trójkątów równobocznych. Nazywa się je „poliamondami”, ponieważ po angielsku dwa trójkąty tworzą „di-amond” (karo, \(\diamondsuit\)). Jako że „diament” nie jest w Polsce zwyczajową nazwą rombu, moglibyśmy nazywać konfiguracje trójkątów „poliapezami”, skoro trzy tworzą „tr(i)-apez”…
Można by się spodziewać, że dla dużych \(n\) obwód „okrągłej masy” trójkątów zacznie zachowywać się „normalnie”, ale w pewnym sensie „skacze” jeszcze bardziej: \[3, 4, 5, 6, 7, \smash{\overset{\triangledown}{6}}, 7, 8, 9, \smash{\overset{\triangledown}{8}}, 9, 10, \smash{\overset{\triangledown}{9}}, 10, 11, \smash{\overset{\triangledown}{10}}, 11, 12, \smash{\overset{\triangledown}{11}}, 12, 13, \smash{\overset{\triangledown}{12}}, 13, \smash{\overset{\triangledown}{12}}, 13, 14, \ldots\] Dopełnieniem tego obrazu grozy jest jawny wzór: \[2\left\lceil \textstyle\frac{n+\sqrt{6n}}{2}\right\rceil-n.\] Jego elementarne wyprowadzenie przedstawimy w części drugiej.