Afiliacja: Politechnika Śląska
Jakie zwierzątko jest schowane w pudełku? Fizyk zakrzyknąłby: Oczywiście, że kot! Natomiast matematyk wie, że może chodzić o pewnego jadowitego gada, któremu poświęcony jest niniejszy odcinek naszego Kąta.
Zacznijmy od teoriografowego uogólnienia pojęcia pudełka. Kostką \(n\)-wymiarową nazywamy graf mający \(2^n\) wierzchołków, każdy z nich etykietujemy jednoznacznie ciągiem binarnym długości \(n\) i przyjmujemy, że dwa wierzchołki są połączone krawędzią, gdy ich ciągi binarne różnią się na dokładnie jednej pozycji – takie dwa wierzchołki nazywamy sąsiednimi.
Informatyk mógłby stwierdzić, że chodzi o ciągi binarne, których odległość Hamminga jest równa \(1.\)
Poniżej pokażemy przykładowe reprezentacje graficzne kostek wymiaru nie większego niż \(4\).
Gdybyśmy dodali dwa warunki geometryczne: 1) każda krawędź ma taką samą, ustaloną, długość i 2) każde dwie sąsiednie krawędzie są wzajemnie prostopadłe, to zaprezentowane kostki moglibyśmy nazwać \(n\)-wymiarowymi hipersześcianami, a załączony rysunek prezentowałby przykładowe rzuty na płaszczyznę kilku najprostszych hipersześcianów. Są nimi, odpowiednio, odcinek, kwadrat, sześcian i tesserakt.

Skonstruujmy ścieżkę w następujący sposób. W rozważanej kostce zaczynamy w dowolnie wybranym wierzchołku i w każdym kroku przechodzimy z ostatnio odwiedzonego wierzchołka do wierzchołka z nim sąsiadującego tak długo, jak jest to możliwe zgodnie z zasadą: po dotarciu do nowego wierzchołka jego poprzednik wraz ze wszystkimi swoimi sąsiadami jest już niedostępny.
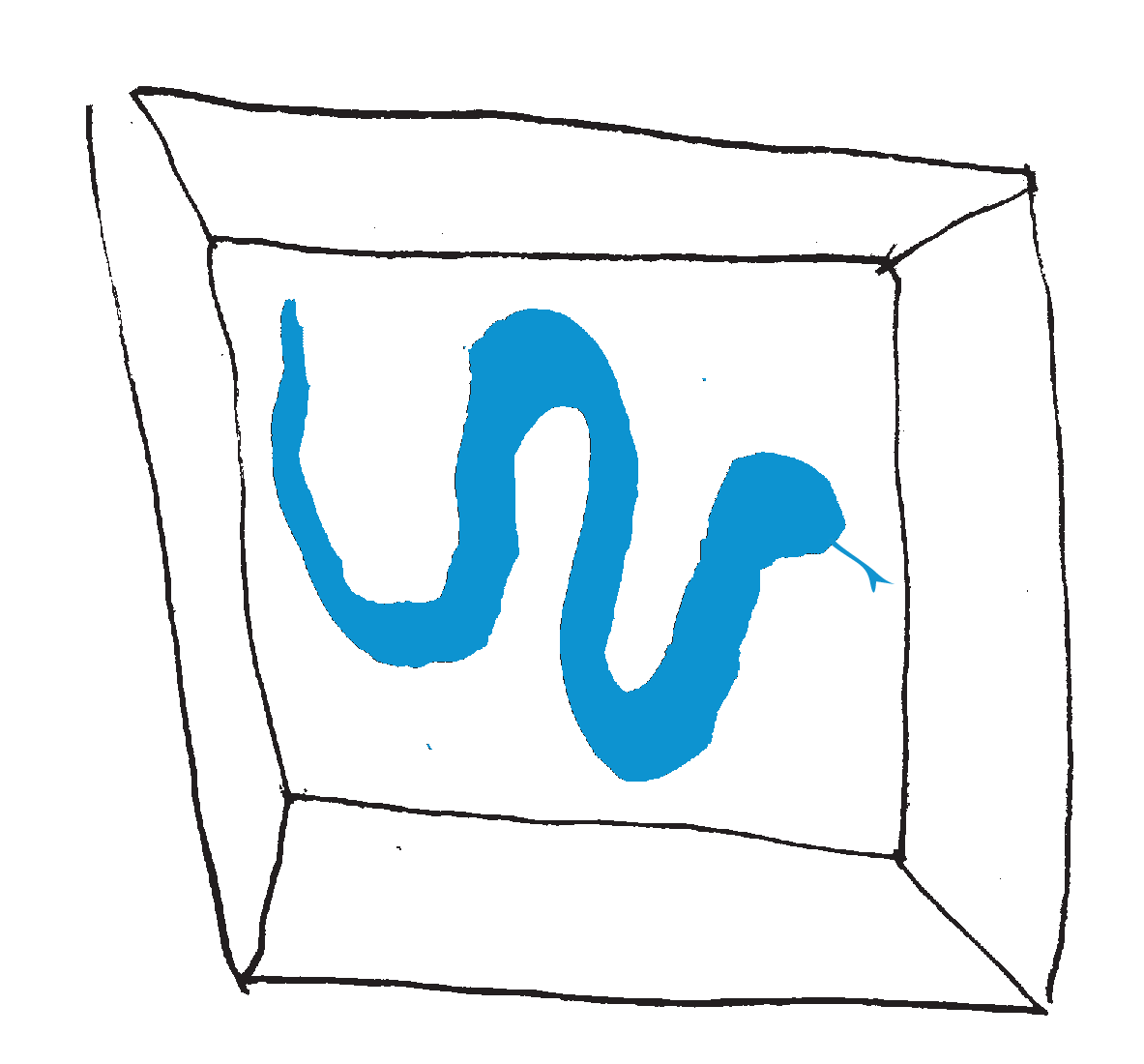
Zademonstrujmy to na przykładzie kostki trójwymiarowej (pudełka):

Otrzymaną w ten sposób ścieżkę nazywamy wężem.
Długością węża nazywamy liczbę krawędzi, przez które przechodzi. Zauważmy, że każdy wąż w trójwymiarowej kostce ma długość równą \(4,\) natomiast w czterowymiarowej można skonstruować węże różnych długości!
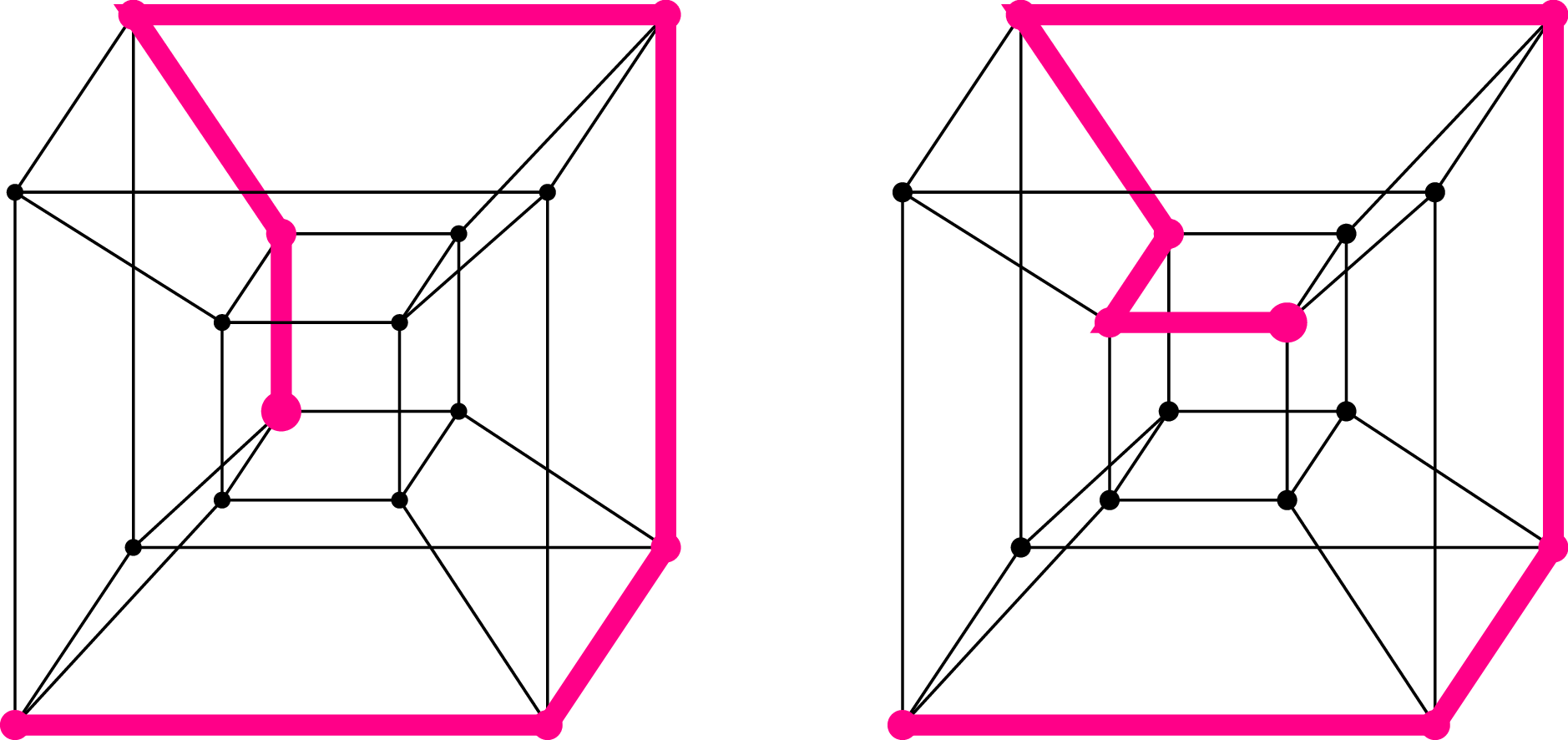
Co ciekawe, dla każdego \(n \ge 2\) można łatwo skonstruować relatywnie krótkiego węża – mającego długość \(2n - 2\) (czy wiesz jak?). Trochę trudniej jest uzasadnić, że krótsze węże nie występują w przyrodzie. Natomiast określenie rozmiaru najdłuższego węża jest nie lada wyzwaniem! Obecnie znamy go tylko dla wymiarów \(n\leqslant8\): \[1,\,2,\,4,\,7,\,13,\,26,\,50,\,98\] (OEIS: A099155). Jak długi może być wąż w \(9\)-wymiarowym pudełku? Jeżeli uda Ci się, Czytelniku, znaleźć odpowiedź na to pytanie, to daj mi znać!
Już wiemy, że w pudełku matematyka można znaleźć to samo, co w kieszeni skąpca. Wracając jednak do kotów – zauważmy, że one też bywają umieszczane w różnych miejscach. Koty w pudełkach są uwielbiane przez fizyków, koty w workach przez hazardzistów, a koty w internecie przez nas wszystkich!