Afiliacja: Uniwersytet im. A. Mickiewicza w Poznaniu
Opublikowany w tym numerze Kącik Początkującego Olimpijczyka nr 66 poświęcony jest zastosowaniu przekształceń afinicznych w rozwiązywaniu zadań olimpijskich. W niniejszym artykule przedstawiam nieco bardziej abstrakcyjne spojrzenie na tę tematykę.
Uogólniona płaszczyzna
Trójkę \[\Pi = (\mathcal{P},\mathcal{L},\thicksim),\] w której \(\mathcal{P}\) i \(\mathcal{L}\) są zbiorami, a \(\thicksim\) jest relacją pomiędzy ich elementami (czyli dla każdego \(P\in\mathcal{P}\) i \(\ell\in\mathcal{L}\) zdanie \(P\thicksim\ell\) jest prawdziwe lub fałszywe), nazywamy uogólnioną płaszczyzną. Jest to faktycznie obiekt niezmiernie ogólny, gdyż elementy zbiorów \(\mathcal{P}\) i \(\mathcal{L}\) mogą być czymkolwiek. Dla przykładu, \(\mathcal{P}\) może być zbiorem potraw, \(\mathcal{L}\) – zbiorem ludzi, a relacja \(P\thicksim\ell\) oznacza, że \(\ell\) lubi \(P.\) I to naprawdę jest pełnoprawna uogólniona płaszczyzna!
Chcąc jednak pozostać nieco bliżej planimetrii, umownie będziemy nazywać:
| \(\mathcal{P}\) | – | zbiorem punktów, |
| \(\mathcal{L}\) | – | zbiorem prostych, |
| \(\thicksim\) | – | relacją incydencji. |
Zamiast punkt \(P\) jest incydentny z prostą \(\ell\) możemy powiedzieć: punkt \(P\) leży na prostej \(\ell\) lub prosta \(\ell\) przechodzi przez punkt \(P\). Ważna uwaga – na płaszczyźnie euklidesowej proste w pewnym sensie są zbiorami punktów i relacja \(\thicksim\) jest po prostu relacją \(\in.\) W ogólności wcale nie musi tak być.
Punkty \(P_1,P_2,\ldots\) nazywamy współliniowymi, gdy istnieje prosta \(\ell,\) która przechodzi przez każdy z nich. Jeśli przez pewien punkt \(P\) przechodzi każda z prostych \(\ell_1,\ell_2,\ldots,\) to nazywamy te proste współpękowymi. Proste \(\ell_1\) i \(\ell_2,\) które nie są współpękowe, nazywamy równoległymi. Piszemy wówczas \(\ell_1\parallel\ell_2.\) Dodatkowo zakładamy, że każda prosta jest równoległa do samej siebie.
Płaszczyzna afiniczna
Aby nieco ograniczyć liczbę obiektów, z którymi będziemy pracować, wprowadzamy pojęcie płaszczyzny afinicznej, która – oprócz tego, że jest uogólnioną płaszczyzną – spełnia dodatkowo trzy aksjomaty. Każdy z nich opiszę krótko, podając, w jakim celu jest wprowadzony i jakie daje korzyści.
Aksjomat (A1). Przez każde dwa punkty przechodzi dokładnie jedna prosta.
Możemy zatem bez wyrzutów sumienia mówić prosta \(AB\), bo taka prosta istnieje i jest dokładnie jedna. Bezpośrednią konsekwencją tego aksjomatu jest to, że każde dwie proste albo są równoległe, albo istnieje dokładnie jeden punkt incydentny z nimi dwiema. W tym drugim przypadku będziemy mówić, że proste się przecinają, a wspomniany punkt nazwiemy ich punktem przecięcia. Jeśli trójka punktów \((A,B,C)\) nie jest współliniowa, to będziemy ją nazywać trójkątem \(ABC\). Jeżeli czwórka punktów \((A,B,C,D)\) spełnia warunki: \(AB\parallel CD\) i \(BC\parallel DA\) oraz te cztery proste są różne, to mówimy o równoległoboku \(ABCD\).
Aksjomat (A2). Dla każdego punktu \(P\) i prostej \(\ell\) istnieje dokładnie jedna prosta przechodząca przez punkt \(P\) i równoległa do prostej \(\ell.\)
Dzięki temu aksjomatowi relacja równoległości jest przechodnia: jeżeli \(\ell_1\parallel\ell_2\) i \(\ell_2\parallel\ell_3,\) to \(\ell_1\parallel\ell_3\) – w przeciwnym razie istniałby punkt, przez który przechodzą dwie proste (\(\ell_1\) i \(\ell_3\)) równoległe do \(\ell_2.\) Możemy zatem podzielić zbiór \(\mathcal{L}\) na takie rozłączne parami podzbiory \(\mathcal{K}_i\) indeksowane elementami \(i\) z pewnego zbioru \(I,\) że zachodzi równoważność \({\ell_1\parallel\ell_2\Leftrightarrow\ell_1,\ell_2\in\mathcal{K}_i}\) dla pewnego \(i\in I.\) Podzbiory te, czyli klasy równoległości prostych, nazywamy kierunkami.
Drugim ważnym wnioskiem jest to, że każdy trójkąt \(ABC\) można uzupełnić do równoległoboku \(ABCD.\) Konstrukcja jest następująca. Niech \(\ell_1\) będzie prostą równoległą do \(AB,\) przechodzącą przez \(C\) oraz niech \(\ell_2\) będzie prostą równoległą do \(BC,\) przechodzącą przez \(A.\) Mamy \(\ell_1\parallel AB\nparallel BC\parallel\ell_2.\) Oznacza to, że proste \(\ell_1\) i \(\ell_2\) należą do różnych kierunków, więc się przecinają. Jeśli \(D\) jest ich punktem przecięcia, to \(ABCD\) jest równoległobokiem.
Aksjomat (A3). Istnieje trójkąt.
Ten aksjomat zapobiega sytuacji zupełnie nieciekawej, w której wszystkie punkty leżą na jednej prostej. Można powiedzieć więcej: dla każdej prostej istnieją co najmniej dwa punkty, przez które ta prosta nie przechodzi – pierwszy wprost z aksjomatu, drugi z konstrukcji równoległoboku. Niech \(ABC\) będzie trójkątem, który uzupełniamy do równoległoboku \(ABCD.\) Dla dowolnej prostej \(\ell\) mamy \(\ell\nparallel AB\) lub \(\ell\nparallel BC.\) W pierwszym przypadku prostą \(\ell\) przecinają proste \(AB\) i \(CD,\) które są różne i równoległe – stąd na prostej \(\ell\) leżą co najmniej dwa punkty. W drugim przypadku jest analogicznie. Zatem każda prosta przechodzi przez co najmniej dwa punkty. Teraz już możemy utożsamić prostą ze zbiorem punktów, przez które przechodzi! Zamiast \(P\thicksim\ell\) możemy teraz pisać \(P\in\ell.\)
Kolineacje płaszczyzny afinicznej
Przekształcenie \(L:\mathcal{P}\to\mathcal{P}\) nazywamy kolineacją płaszczyzny \(\Pi\), jeśli jest bijekcją oraz spełnia następujący warunek: dla każdej trójki współliniowych punktów \(A,\) \(B,\) \(C\) punkty \(L(A),\) \(L(B),\) \(L(C)\) również są współliniowe.
Twierdzenie. Niech \(L\) będzie kolineacją płaszczyzny afinicznej. Wówczas dla każdej prostej \(\ell\in\mathcal{L}\) zbiór \(L(\ell)\) też jest prostą.
Mówiąc prościej, obrazami prostych są proste.
Dowód. Niech punkty \(A\) i \(B\) leżą na prostej \(\ell.\) Przez punkty
primowane zawsze oznaczać będziemy obrazy punktów nieprimowanych. Oznaczmy
\(\ell'=A'B'.\) Z definicji kolineacji wynika, że dla każdego \(X\in\ell\) zachodzi
\(X'\in\ell',\) więc \(L(\ell)\subseteq\ell'.\) Trzeba jeszcze
wykazać przeciwne zawieranie. Przypuśćmy, że tak nie jest i niech punkt
\(C\not\in\ell,\) ale \(C'\in\ell'.\) Ponieważ \({A',B',C'\in\ell'},\) obrazy prostych
\(AB,\) \(BC\) i \(CA\) są zawarte w \(\ell'.\) Uzupełnijmy trójkąt \(ABC\) do
równoległoboku \(ABCD.\)
Niech \(P\) będzie dowolnym punktem różnym od \(A,\) \(B,\)
\(C,\) \(D.\) Wówczas \(CP\nparallel AB\) lub \(AP\nparallel BC.\) W pierwszym przypadku
proste \(CP\) i \(AB\) przecinają się w pewnym punkcie \(Q.\) Ponieważ \(Q\) leży na
\(AB,\) mamy \(Q'\in\ell'.\) Również \(C'\in\ell',\) więc \(P'\in\ell'.\)
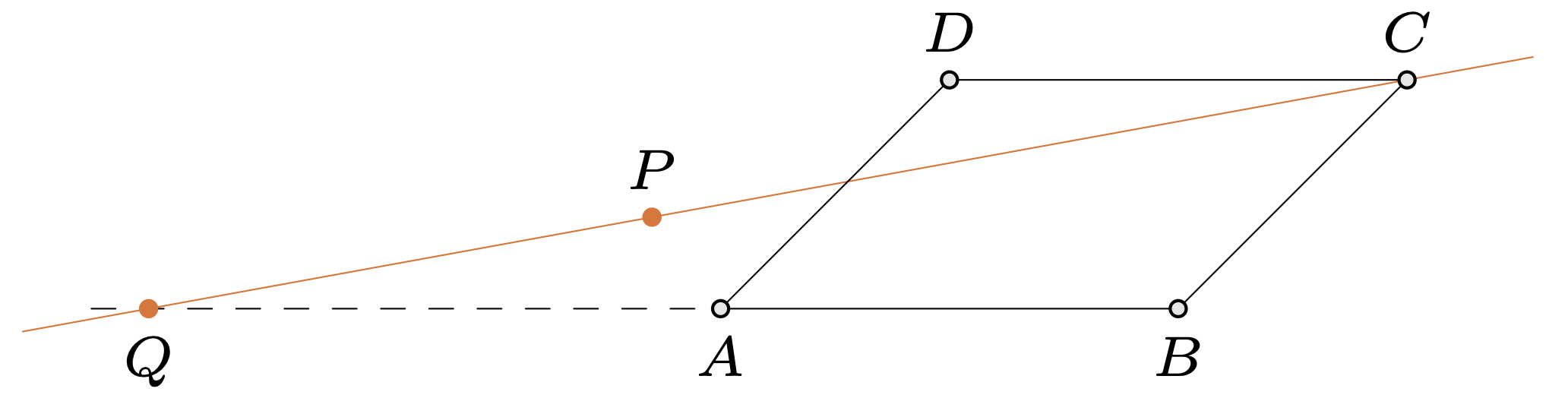
Drugi przypadek jest analogiczny. Wnioskujemy stąd, że \(L(\mathcal{P}\setminus\{D\})\subseteq\ell'.\) Funkcja \(F:\mathcal{P}\to\mathcal{P}\) jest bijekcją, więc co najwyżej jeden punkt (\(D'\)) nie leży na prostej \(\ell'.\) Jest to poszukiwana sprzeczność, bo powinny być co najmniej dwa takie punkty.\(\Box\)
Jednym z najważniejszych wniosków jest to, że przekształcenie odwrotne do kolineacji płaszczyzny afinicznej również jest kolineacją płaszczyzny afinicznej. Kolejne, nietrudne wnioski pozostawiam Czytelnikowi: obrazami/przeciwobrazami trójkątów są trójkąty, par prostych równoległych – pary prostych równoległych, par prostych przecinających się – pary prostych przecinających się, a równoległoboków – równoległoboki.
Płaszczyzna afiniczna \(\mathbb{R}^2\)
Od teraz będziemy prowadzić rozważania dla płaszczyzny euklidesowej \(\mathbb{R}^2\), która, jak łatwo sprawdzić, z punktami \(P=(x,y)\) oraz prostymi \(\ell=\{(x,y):{ax+by+c=0}\}\) \((a^2+b^2\neq0)\) spełnia definicję płaszczyzny uogólnionej z relacją \(\in\) oraz aksjomaty płaszczyzny afinicznej. Celem jest następujące
Twierdzenie. Kolineacje płaszczyzny \(\mathbb{R}^2\) są tym samym, co przekształcenia afiniczne, czyli odwzorowania bijektywne \(F:\mathbb{R}^2\to\mathbb{R}^2,\) spełniające następujące warunki:
obrazami prostych są proste;
jeśli \(\overrightarrow{SX}=x\overrightarrow{SA}\) dla pewnej liczby rzeczywistej \(x,\) to \(\overrightarrow{F(S)F(X)}=x\overrightarrow{F(S)F(A)}.\)
Dowód. Każde przekształcenie afiniczne jest kolineacją – wynika to z warunku (1). Załóżmy zatem, że przekształcenie \(L\) jest kolineacją \(\mathbb{R}^2.\) Warunek (1) już udowodniliśmy, dowód warunku (2) podzielimy na kilka kroków. Tak jak poprzednio, niech punkty primowane będą obrazami punktów nieprimowanych.
Krok 1. Jeśli \(\overrightarrow{A_1B_1}=\overrightarrow{A_2B_2},\)
to \(\overrightarrow{A_1'B_1'}=\overrightarrow{A_2'B_2'}.\)
Jeżeli proste \(A_1B_1\) i \(A_2B_2\) są różne, to \(A_1B_1B_2A_2\) jest
równoległobokiem, więc jego obraz \(A_1'B_1'B_2'A_2'\) też jest równoległobokiem.
W przeciwnym razie rozważamy dodatkowy wektor \(\overrightarrow{A_3B_3},\) który
leży poza prostą \(A_1B_1.\) Korzystając dwukrotnie z pierwszego przypadku, mamy \(\overrightarrow{A_1'B_1'}=\overrightarrow{A_3'B_3'}=\overrightarrow{A_2'B_2'}.\)
Niech \(V\) będzie zbiorem wektorów swobodnych, dwuwymiarowych, o współrzędnych rzeczywistych. Korzystając z powyższego, możemy zdefiniować przekształcenie \(T:V\to V\) indukowane przez kolineację \(L\) w następujący sposób: \(T(\vec{v})=\overrightarrow{A'B'},\) dla punktów \(A\) i \(B\) spełniających równość \(\vec{v}=\overrightarrow{AB}.\) Przekształcenie \(T\) jest poprawnie i jednoznacznie określone za pomocą \(L.\) Jeśli znamy \(T\) oraz wiemy, że \(L(S)=S',\) to możemy jednoznacznie odtworzyć przekształcenie \(L\) za pomocą równości \(\overrightarrow{S'X'}=T(\overrightarrow{SX}).\)
Krok 2. \(T(\vec{u}+\vec{v})=T(\vec{u})+T(\vec{v})\) oraz
\(T(t\vec{v})=tT(\vec{v})\) dla każdego wymiernego \(t.\)
Rozważmy takie punkty \(A,\) \(B,\) \(C,\) że \(\vec{u}=\overrightarrow{AB}\) i
\(\vec{v}=\overrightarrow{BC}.\) Wtedy \[T(\vec{u}+\vec{v}) =
T(\overrightarrow{AC}) = \overrightarrow{A'C'} = \overrightarrow{A'B'} +
\overrightarrow{B'C'} = T(\vec{u})+T(\vec{v}).\] Dalej indukcyjnie \(T((n+1)\vec{v}) = T(n\vec{v}+\vec{v}) = T(n\vec{v})+T(\vec{v}) = nT(\vec{v})+T(\vec{v}) = (n+1)T(\vec{v})\) z warunkiem początkowym \(n=1.\) Stąd \(mT(\frac nm\vec{v})=\newline = T(n\vec{v}) = nT(\vec{v}),\) więc \(T(\frac nm\vec{v}) = \frac nm T(\vec{v}).\) Pozostaje zauważyć, że \(T(-\vec{v})=-T(\vec{v}).\)
Rozważmy proste \(\ell_a\) i \(\ell_b\) przecinające się w punkcie \(S.\) Niech \(A,B\neq S\) będą odpowiednio punktami na prostych \(\ell_a\) i \(\ell_b\) oraz niech \(\vec{a}=\overrightarrow{SA}\) i \(\vec{b}=\overrightarrow{SB}.\) Określmy funkcję \(\phi:\mathbb{R}\to\mathbb{R}\) w taki sposób, że \({T(x\vec{a})=\phi(x)T(\vec{a})}\) dla każdego \(x\in\mathbb{R}.\) Analogicznie niech \(T(y\vec{b})=\psi(y)T(\vec{b}).\) Z poprzedniego kroku wynika, że \(\psi(t)=\phi(t)=t\) dla wszystkich \(t\) wymiernych.
Krok 3. \(\phi=\psi.\)
Niech \(x=y\) oraz \(\overrightarrow{SX}=x\vec{a}\) i
\(\overrightarrow{SY}=y\vec{b}.\) Mamy \(XY\parallel AB,\) więc \(X'Y'\parallel A'B'.\) Stąd \(\phi(x)=\psi(y).\)

Krok 4. \(\phi(x+y)=\phi(x)+\phi(y)\) dla \(x\) i \(y\) rzeczywistych.
Zachodzą równości: \(\phi(x)T(\vec{a})+\phi(y)T(\vec{a}) = T(x\vec{a})+\newline+T(y\vec{a}) = T(x\vec{a}+y\vec{a}) =
T((x+y)\vec{a})=\phi(x+y)T(\vec{a}).\)
Krok 5. Funkcja \(\phi\) jest niemalejąca.
Rozważmy wektor \(\vec{v}=x\vec{a}+\vec{b}.\) Wektor \(x\vec{v}\) jest do niego równoległy, więc wektory \(T(\vec{v})=\phi(x)T(\vec{a})+T(\vec{b})\) i \(T(x\vec{v})=\phi(x^2)T(\vec{a})+\phi(x)T(\vec{b})\) są równoległe. Mają one zatem proporcjonalne współczynniki przy \(T(\vec{a})\) i \(T(\vec{b}),\) co prowadzi do równości \(\phi(x^2)=\phi(x)^2.\) Wnioskujemy stąd, że jeśli \(t\ge0,\) to \(\phi(t)=\phi(\sqrt{t})^2\ge0.\) Dla \(y\ge x\) zapiszmy \(y=x+t.\) Mamy \(\phi(y)=\phi(x+t)=\phi(x)+\phi(t)\ge\phi(x).\)
Krok 6. \(\phi(t)=t\) dla każdego \(t\in\mathbb{R}.\)
Funkcja \(\phi\) jest niemalejąca oraz identycznościowa na zbiorze liczb wymiernych, więc jest identycznościowa na zbiorze liczb rzeczywistych, gdyż zbiór liczb wymiernych jest w nim gęsty.
Zauważmy, że teza kroku 6 tłumaczy się na równość z warunku (2). Uff, koniec dowodu!