Afiliacja: Uniwersytet im. A. Mickiewicza w Poznaniu
Przekształcenia afiniczne to bijekcje \(F:\mathbb{R}^2\to\mathbb{R}^2\) spełniające następujące warunki:
obrazami prostych są proste;
jeśli \(\overrightarrow{SX}=x\overrightarrow{SA}\) dla \(x\in\mathbb{R},\) to \(\overrightarrow{F(S)F(X)}=x\overrightarrow{F(S)F(A)}.\)
Aby wykazać, że dane przekształcenie płaszczyzny \(\mathbb{R}^2\) jest afiniczne, wystarczy zweryfikować, że jest bijektywne i zachowuje współliniowość punktów (co uzasadniam w artykule Proste i punkty w świecie abstrakcji w tym numerze Delty). Jest zatem oczywiste, że wszystkie homometrie (podobieństwa) są przekształceniami afinicznymi. Są jednak jeszcze inne przekształcenia afiniczne. Oto przykłady:
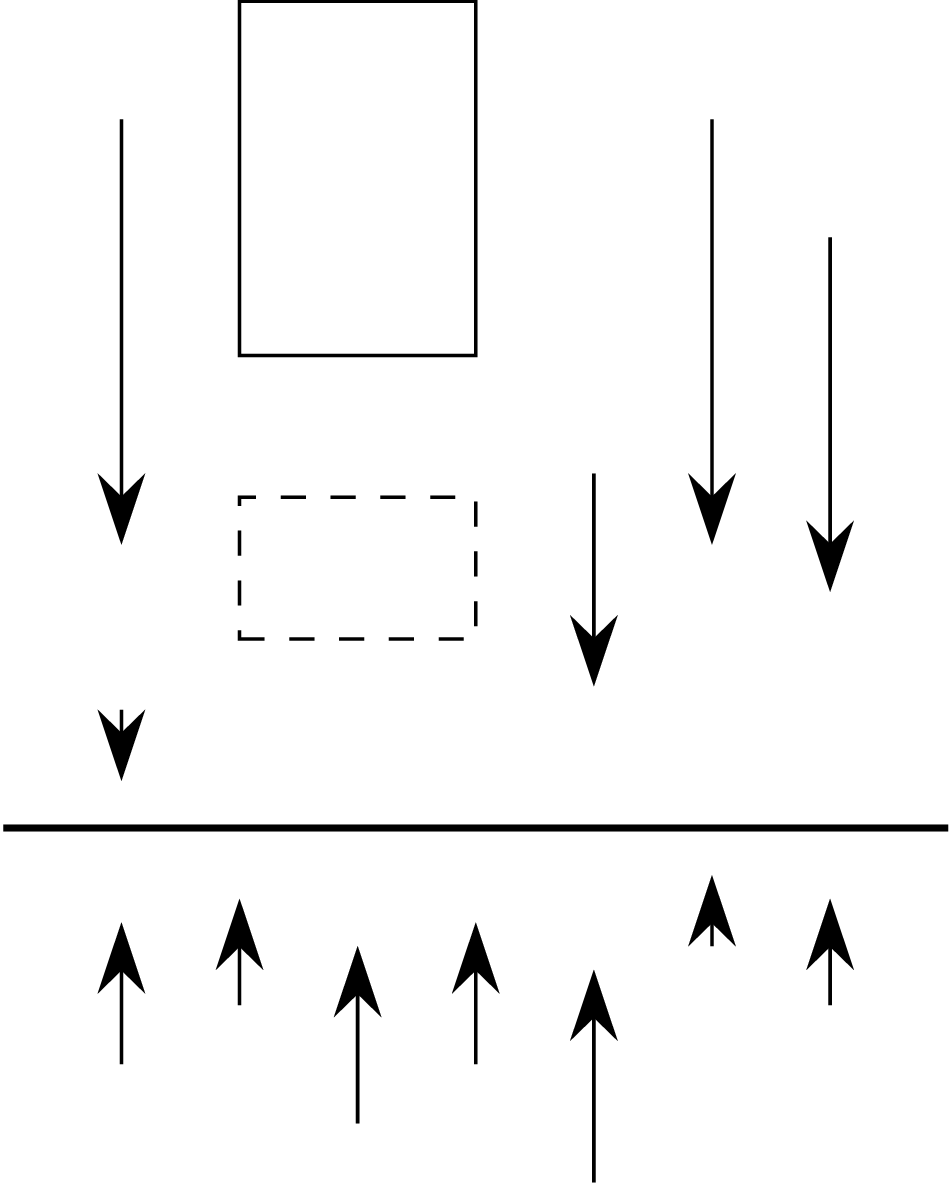
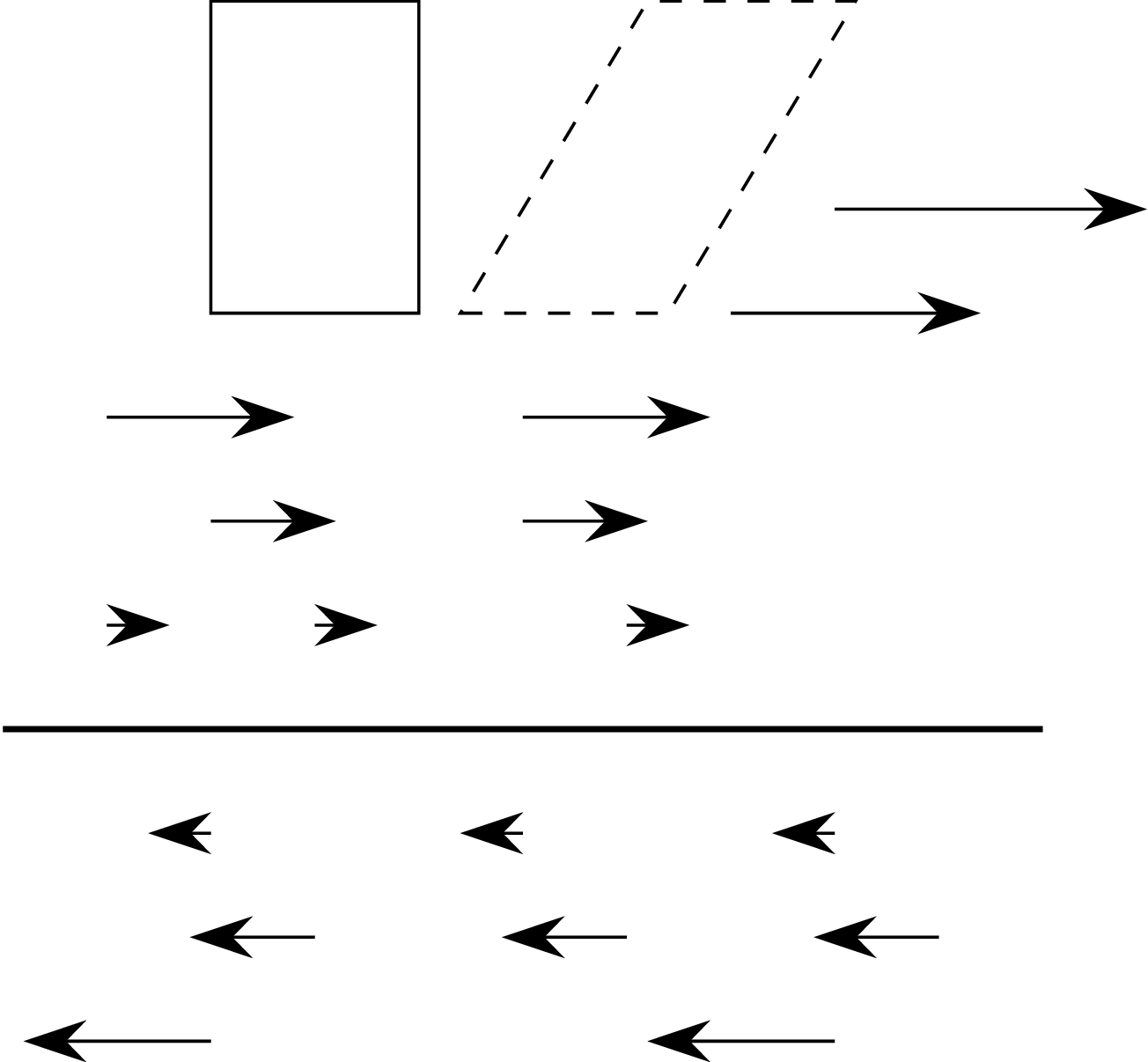
Po lewej stronie widzimy powinowactwo prostokątne, a po prawej pochylenie. Jeśli zaznaczona prosta ma równanie \(y=0,\) to dla powinowactwa prostokątnego mamy \((x,y)\mapsto(x,\lambda y)\) (\(\lambda\neq0\) jest współczynnikiem przekształcenia), a dla pochylenia \((x,y)\mapsto(x+\lambda y,y).\)
Niech \(ABC\) i \(A'B'C'\) będą niezdegenerowanymi trójkątami. Niech \(F_1\) będzie homometrią, która przekształca odcinek \(AB\) w odcinek \(A'B',\) a punkt \(C\) w pewien punkt \(C_1.\) Przez \(F_2\) oznaczmy powinowactwo prostokątne względem prostej \(A'B',\) które punkt \(C_1\) przekształca w taki punkt \(C_2,\) że \(C_2C'\parallel A'B'.\) Na koniec niech \(F_3\) będzie pochyleniem względem prostej \(A'B',\) dla którego \(F_3(C_2)=C'.\) Przekształcenie afiniczne \({F=F_3\circ F_2\circ F_1}\) przeprowadza punkty \(A,\) \(B,\) \(C\) w punkty, odpowiednio, \(A',\) \(B',\) \(C',\) więc każdy trójkąt można afinicznie przekształcić w każdy inny. Co więcej, jest to jedyne takie przekształcenie, gdyż jeśli \({F(X)=X'}\) i \({\overrightarrow{CX}=x\overrightarrow{CA}+y\overrightarrow{CB}},\) to \({\overrightarrow{C'X'}=x\overrightarrow{C'A'}+y\overrightarrow{C'B'}}.\)
Niech \(s\) będzie skalą homometrii \(F_1,\) a \(\lambda\) współczynnikiem
powinowactwa prostokątnego \(F_2.\) Wówczas \(F\) przekształci figurę o polu \(P\) w figurę o polu \(s^2|\lambda|\cdot P.\) Wynika z tego, że przekształcenia afiniczne zachowują proporcję pól.
Jeśli założenia i teza pewnego twierdzenia nie zmieniają się po zastosowaniu do nich przekształcenia afinicznego, to nazywamy je afinicznym. Takie twierdzenie wystarczy udowodnić dla jednej, najwygodniejszej konfiguracji geometrycznej i jest ono wówczas dowiedzione dla każdej konfiguracji, która jest z nią afiniczna.
Prosty przykład: środkowe trójkąta dzielą go na sześć trójkątów o równych polach. Jest to twierdzenie afiniczne, gdyż po przekształceniu afinicznym środkowe pozostają środkowymi (zachowanie współliniowości i proporcji na prostej) oraz trójkąty o równych polach są przekształcone właśnie na takie trójkąty. Wystarczy więc wykazać je dla trójkąta równobocznego, bo każdy trójkąt jest afiniczny z każdym, w szczególności z równobocznym. A środkowe dzielą trójkąt równoboczny na sześć trójkątów przystających.
Zadania
1. Dany jest trójkąt \(ABC.\) Na odcinku \(AB\) leżą punkty \(R_1\) i \(R_2\) spełniające równość \(|AR_1|=|BR_2|.\) Analogiczną własność mają punkty \(P_1\) i \(P_2\) na odcinku \(BC\) oraz \(Q_1\) i \(Q_2\) na odcinku \(CA.\) Wykazać, że trójkąty \(P_1Q_1R_1\) i \(P_2Q_2R_2\) mają równe pola.
Wystarczy wykazać to dla trójkąta równobocznego \(ABC.\) Można obliczyć \([P_1Q_1R_1]=[ABC]-[AR_1Q_1]-[BR_1P_1]-[CQ_1P_1],\) stosując wzór \([AR_1Q_1]=\frac{\sqrt3}4|AR_1|\cdot|AQ_1|\) i analogiczne dla pozostałych trójkątów. Tak samo obliczamy \([P_2Q_2R_2].\)
2. Na bokach \(BC,\) \(CA,\) \(AB\) trójkąta \(ABC\) leżą punkty, odpowiednio, \(P,\) \(Q,\) \(R\); zachodzi ponadto równość \(\frac{|AR|}{|RB|}=\frac{|BP|}{|PC|}=\frac{|CQ|}{|QA|}.\) Udowodnić, że trójkąty \(ABC,\) \(PQR\) oraz trójkąt wyznaczony przez proste \(AP,\) \(BQ,\) \(CR\) mają wspólny środek ciężkości.
Również wystarczy przeprowadzić dowód dla trójkąta równobocznego \(ABC.\) Aby się przekonać, że pozostałe dwa trójkąty też są równoboczne i mają ten sam środek co \(ABC,\) wystarczy obrócić trójkąt \(ABC\) o \(120^\circ\) wokół jego środka.
3. Dany jest równoległobok \(ABCD.\) Na odcinkach \(AB,\) \(BC,\) \(CD\) leżą, odpowiednio, punkty \(K,\) \(L,\) \(M,\) przy czym \(\frac{|AK|}{|KB|}=\frac{|BL|}{|LC|}=\frac{|CM|}{|MD|}.\) Prosta \(m\parallel KL\) przechodzi przez punkt \(B.\) Prosta \(l\parallel KM\) przechodzi przez punkt \(C.\) Prosta \(k\parallel ML\) przechodzi przez punkt \(D.\) Dowieść, że proste \(k,\) \(m,\) \(l\) przecinają się w jednym punkcie.
Każdy równoległobok jest afiniczny z kwadratem przez złożenie właściwego pochylenia i powinowactwa prostokątnego. W przypadku gdy \(ABCD\) jest kwadratem, można wykazać, że każde dwie spośród prostych \(k,\) \(l,\) \(m\) przecinają się na okręgu opisanym na tym kwadracie.
4. Na boku \(AC\) trójkąta \(ABC\) wybrano punkt \(Q.\) Punkt \(P\) jest środkiem odcinka \(BC.\) Odcinki \(AP\) i \(BQ\) przecinają się w punkcie \(T.\) Punkt \(R\) jest środkiem odcinka \(AT,\) natomiast punkt \(S\) leży na odcinku \(BT\) i spełnia równość \(|BS|=|QT|.\) Dowieść, że \(PS \parallel QR.\)
Można zastosować przekształcenie afiniczne, które trójkąt \(AQT\) przekształca w trójkąt równoramienny z kątem prostym przy wierzchołku \(Q.\) Wtedy punkt \(P\) jest środkiem okręgu opisanego na trójkącie \(BCQ,\) więc \(|SP|=|TP|,\) co prowadzi do \(|\measuredangle SPT|=90^\circ.\)