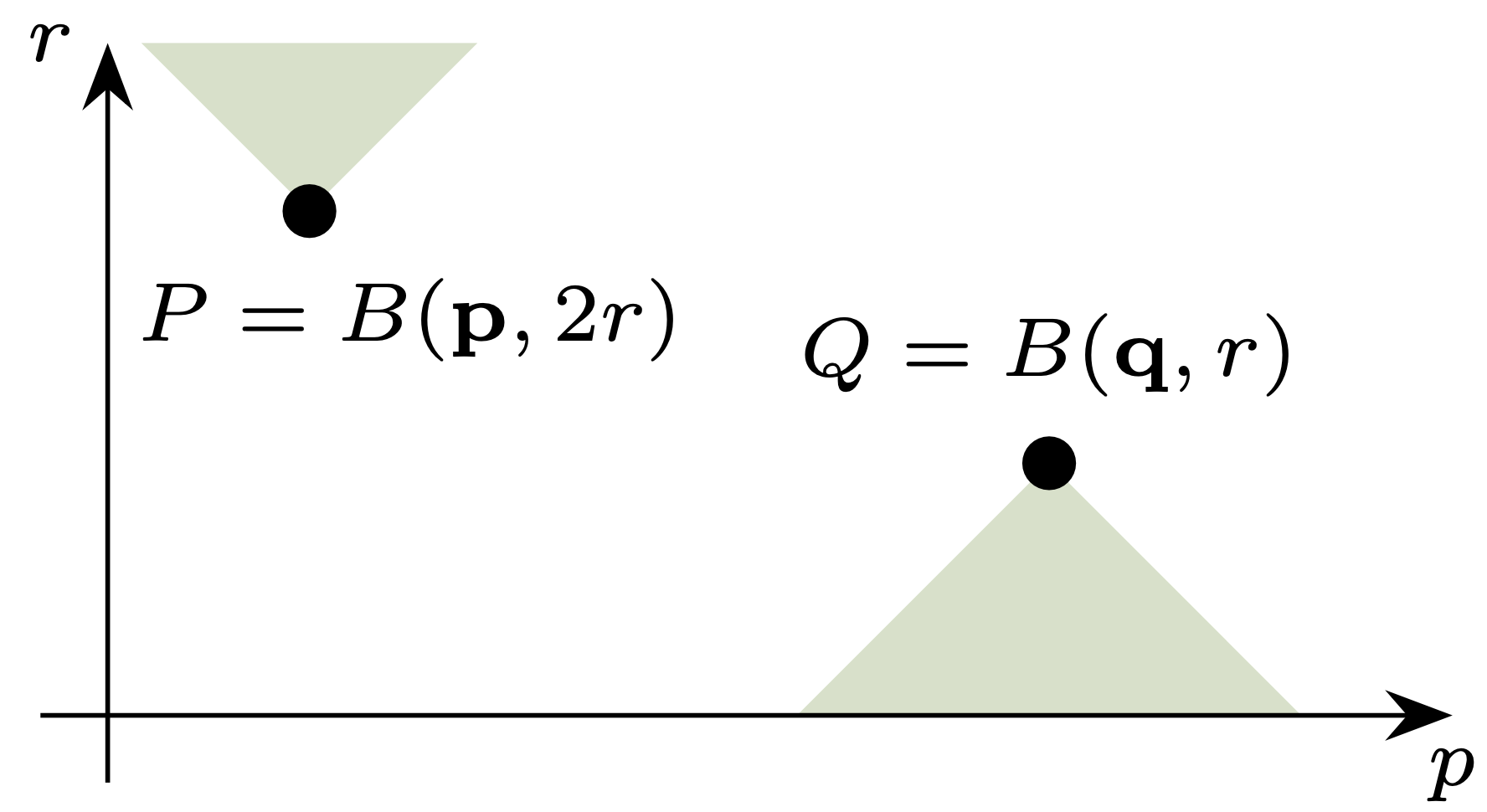Afiliacja: Wydział Matematyki, Informatyki i Mechaniki UW
W Internecie łatwo można znaleźć quizy, których rozwiązanie pozwala odpowiedzieć na ważne pytania: z którą księżniczką Disneya mogę się utożsamiać?, które warzywo najlepiej mnie opisuje?, do którego z czterech domów Hogwartu pasuję? Postanowiłem dodać swoje trzy grosze, pytając Czytelników Delty o geometrię przestrzeni kół. Rzecz jest subiektywna, więc nie ma złych odpowiedzi. Zdajmy się więc na Tiarę Przydziału!
W poniższych pytaniach przez \(d(P,Q)\) należy rozumieć odległość między kołami \(P\) i \(Q.\) Z podanych odpowiedzi wybieramy tę, która według nas najlepiej opisuje sytuację na rysunkach niżej. O przydziale decyduje wybrany symbol; może się okazać, że pasuje więcej niż jeden dom.
Pytanie 1
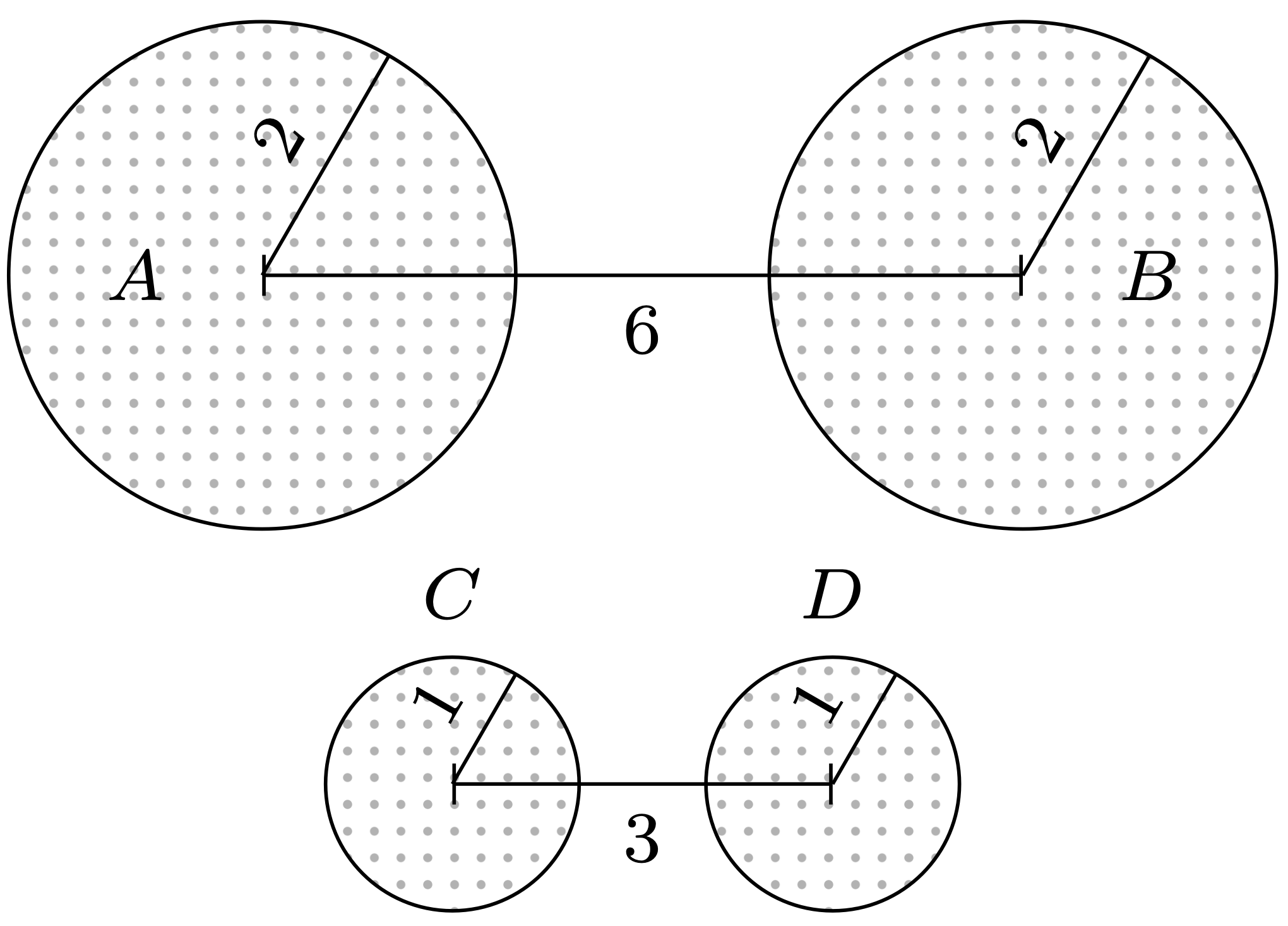
\(d(A,B) = d(C,D)\)
\(d(A,B) = 2 \cdot d(C,D)\)
inna odpowiedź
Pytanie 2
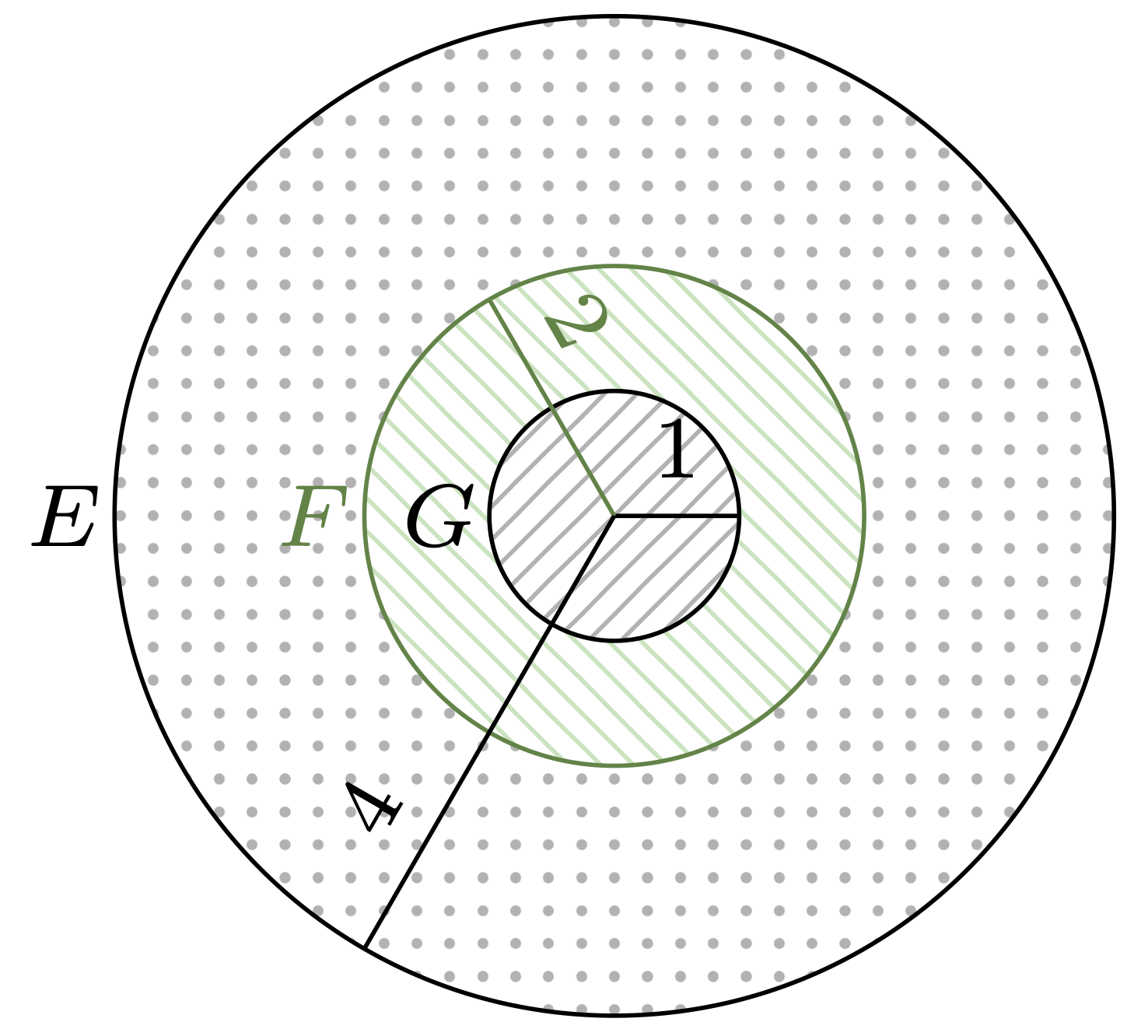
\(d(E,F) = d(F,G)\)
\(d(E,F) = 2 \cdot d(F,G)\)
obie powyższe odpowiedzi, gdyż \(d(E,F) = 0 = d(F,G)\)
inna odpowiedź
Sprawdź swój wynik!
\(\heartsuit\) Hufflepuff! Twoje rozumienie odległości między kołami trudno uchwycić poprzez proste zależności, ale na pewno okaże się ono przydatne w momencie, w którym świat magii będzie tego najbardziej potrzebował. Tak trzymaj!
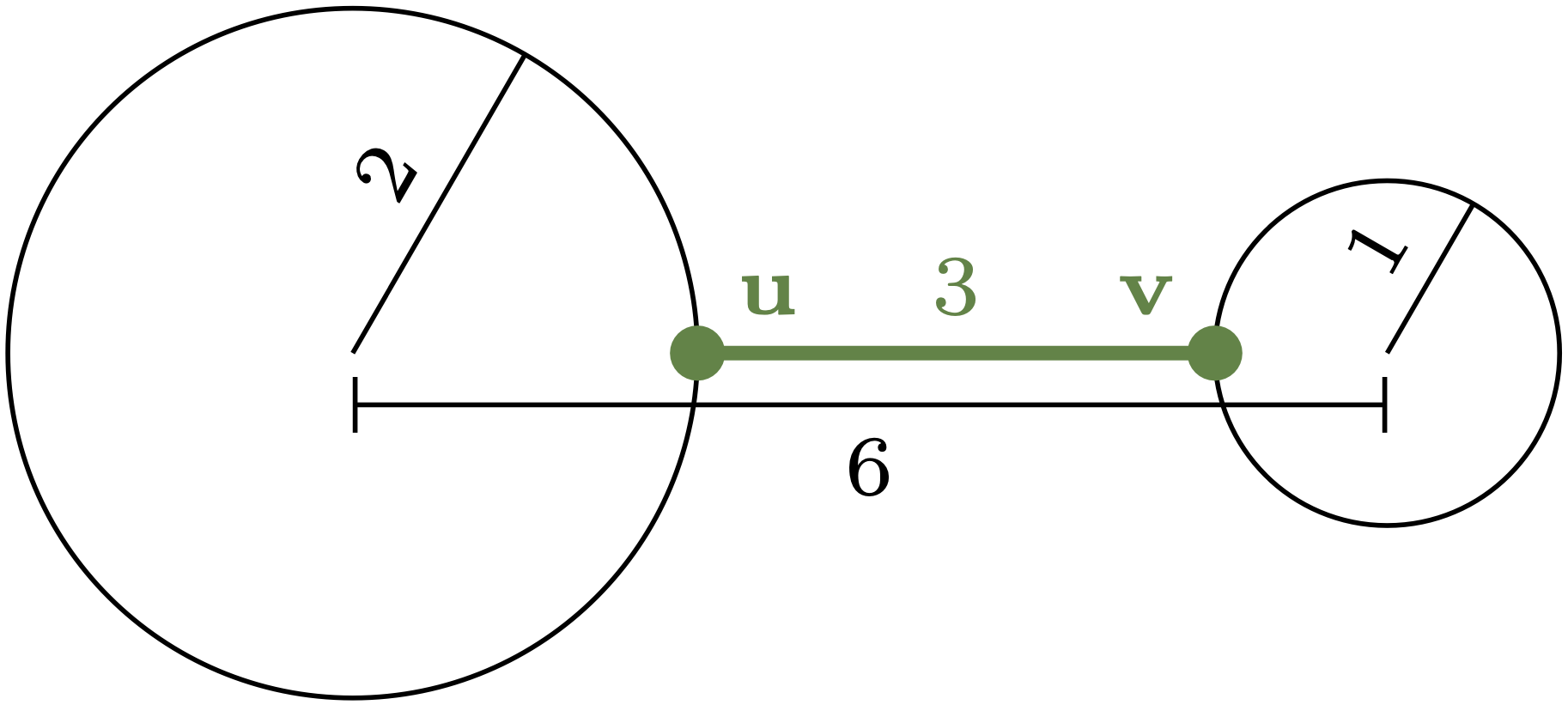
\(\spadesuit\) Gryffindor! Bardzo możliwe, że przez odległość \(d(P,Q)\) rozumiesz długość najkrótszego odcinka łączącego jakiś punkt \(\mathbf{u} \in P\) z jakimś punktem \(\mathbf{v} \in Q\) (rys. 1). Wtedy \(d(A,B) = 2,\) \(d(C,D) = 1,\) natomiast dowolne dwie przecinające się koła są w zerowej odległości. Brawo! Pamiętaj tylko, że tak określona odległość nie jest metryką, czyli nie mierzy, jak bardzo dwa koła się różnią – dwa koła mogą się różnić diametralnie, a nadal być odległe o \(0.\)
Rys. 1. Według typowego Gryfona powyższe koła są odległe o \(3,\) gdyż taką długość ma najkrótszy odcinek je łączący
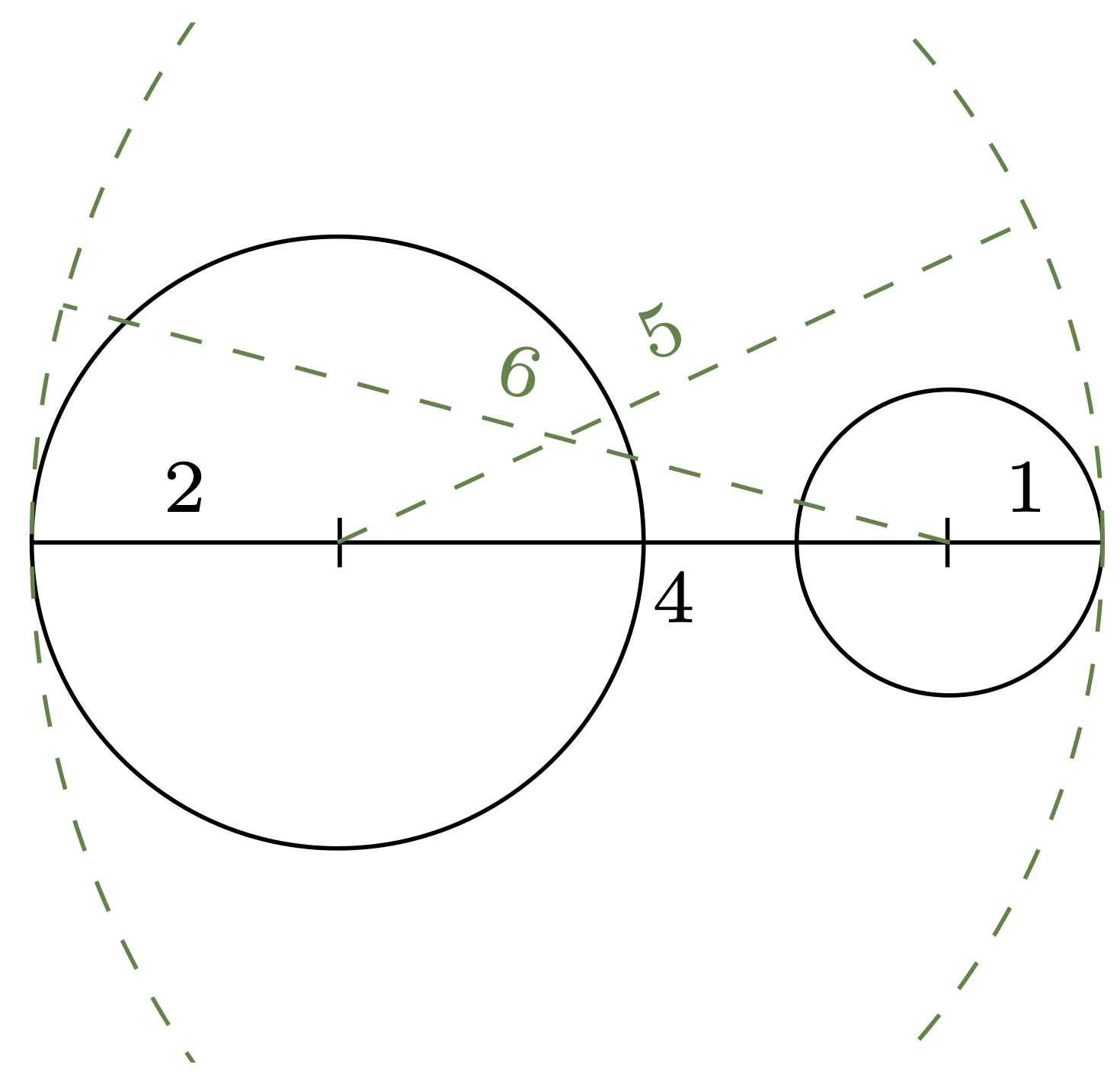
\(\diamondsuit\) Ravenclaw! Niewykluczone, że Twoje rozumienie \(d(P,Q)\) pokrywa się z odległością zdefiniowaną przez Felixa Hausdorffa (1868–1942). Mierzysz, o ile trzeba powiększyć koło \(P,\) żeby pochłonęło \(Q,\) potem odwrotnie – o ile należy powiększyć \(Q\) – a na koniec wybierasz większą z tych dwóch wielkości (rys. 2). Wtedy \(d(A,B) = 6,\) \(d(C,D) = 3\) oraz \(d(E,F) = 2,\) \(d(F,G) = 1.\) Świetnie!
Rys. 2. Żeby lewe koło pokryło prawe, trzeba zwiększyć promień o \(3,\) natomiast żeby prawe pokryło lewe – aż \(5.\) Według Krukonów koła te są więc odległe o \(5\)
Dzięki opisanej tu metryce Hausdorffa można mierzyć odległość między rozmaitymi zbiorami, ale w przypadku kół łatwo ją wyrazić jawnym wzorem. Jeśli dane są koła \(P = B(\mathbf{p},r_1)\) i \(Q = B(\mathbf{q},r_2)\) (\(\mathbf{p},\mathbf{q}\) to ich środki, a \(r_1,r_2\) – promienie), to widać, że najmniejsze koło o środku w \(\mathbf{p}\) i zawierające \(Q\) ma promień \(|\mathbf{p}-\mathbf{q}|+r_2\); koło \(P\) trzeba więc powiększyć o \({|\mathbf{p}-\mathbf{q}|+r_2-r_1}\) (lub \(0,\) jeśli ta liczba jest ujemna). Podobnie koło \(Q\) trzeba powiększyć o \({\max(0,|\mathbf{p}-\mathbf{q}|+r_1-r_2)},\) jako większą z tych liczb otrzymujemy więc \({d(P,Q) = |\mathbf{p}-\mathbf{q}|+|r_1-r_2|}.\)
Pojęcie odległości (bardziej fachowo: metryki) pozwala myśleć o zbiorze wszystkich kół na płaszczyźnie jako o przestrzeni, a o kołach jako o jej punktach. Jest jasne, że odległość Hausdorffa \(d(P,Q)\) jest zerowa jedynie wtedy, gdy koła \(P\) i \(Q\) są identyczne; spełniona jest też nierówność trójkąta: \({d(P,Q) \le d(P,S) + d(S,Q)}\) dla wszystkich \(P,Q,S\) (zad. 1). Te własności powodują, że \(d\) można śmiało wykorzystywać do opisu geometrii przestrzeni kół.
Zadanie 1. Uzasadnić, że jeśli \(B(\mathbf{p}_1,r_1) \subseteq B(\mathbf{p}_2,r_2+a)\) oraz \(B(\mathbf{p}_2,r_2) \subseteq B(\mathbf{p}_3,r_3+b),\) to \(B(\mathbf{p}_1,r_1) \subseteq B(\mathbf{p}_3,r_3+a+b).\) Wywnioskować, że nierówność trójkąta jest spełniona dla metryki Hausdorffa.
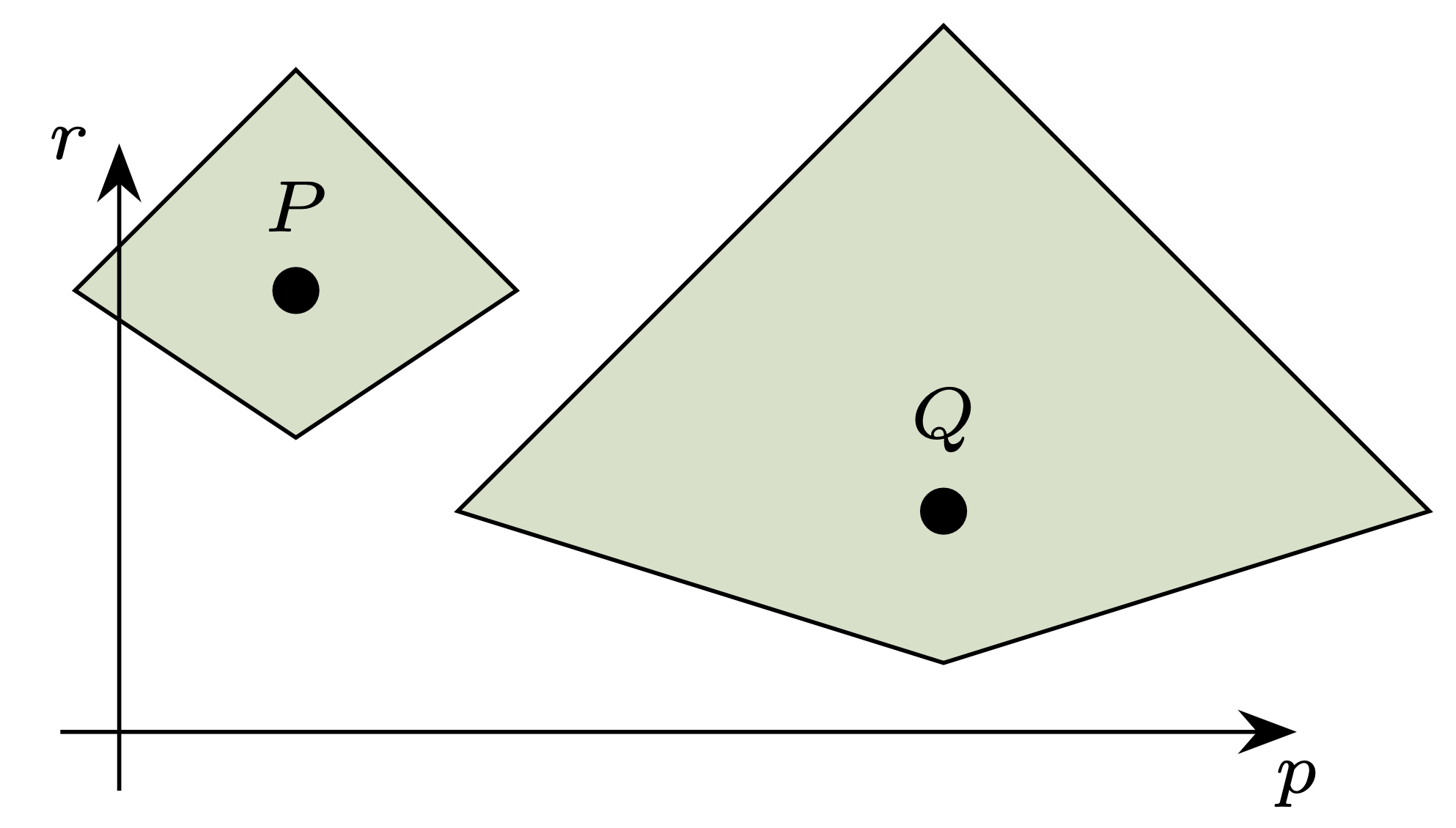
Rys. 3. Punkt \(P\) reprezentuje pewne koło, a obszar zaznaczony powyżej niego odpowiada wszystkim kołom zawierającym \(P.\) Podobnie punkt \(Q\) to koło o dwukrotnie mniejszym promieniu niż \(P,\) a obszar poniżej to wszystkie koła zawierające się w \(Q\)
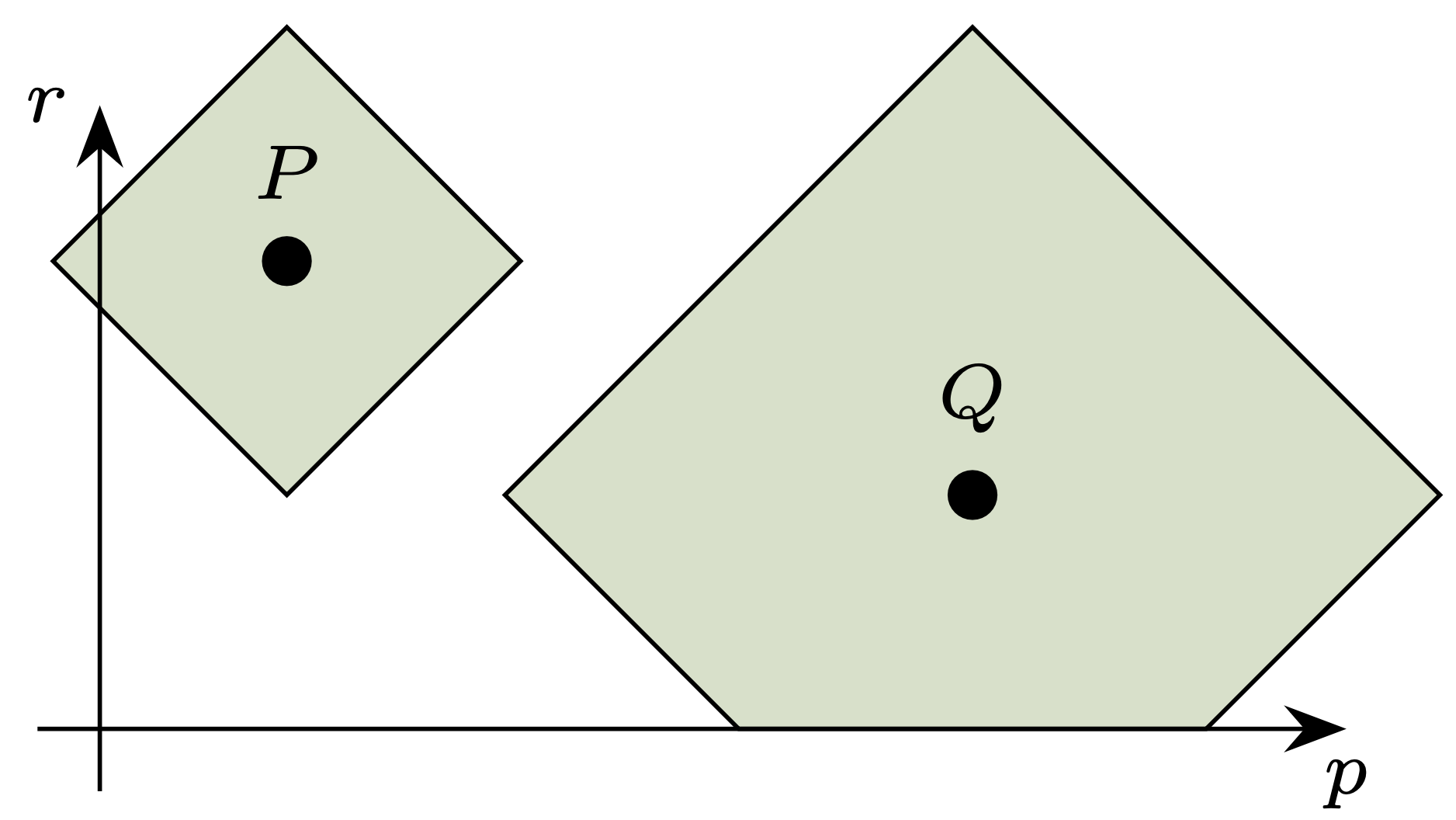
Rys. 4. Zaznaczono wszystkie koła odległe (w metryce Hausdorffa) od \(P\) o najwyżej \(r\) oraz te odległe od \(Q\) o najwyżej \(2r\)
Okazuje się, że jest to geometria dobrze nam znana. Przyporządkujmy mianowicie kołu \(B(\mathbf{p},r) \subseteq \mathbb{R}^2\) (o środku w \(\mathbf{p}= (p_1,p_2)\)) trójkę liczb \((p_1,p_2,r),\) a więc punkt w górnej połowie przestrzeni \(\mathbb{R}^3.\) Pomijając jeden wymiar, możemy wtedy reprezentować przestrzeń kół jak na rysunku 3. Możemy też zilustrować wybraną metrykę, wybierając punkt \(P\) (czyli jakieś koło) i promień \(R > 0,\) a następnie rysując obszar odpowiadający wszystkim punktom-kołom odległym od \(P\) o najwyżej \(R\) (rys. 4). Jak wspomniałem, na rysunku brakuje jednego wymiaru, a w rzeczywistości taki obszar ma kształt podwójnego stożka. Jeśli jednak chcieć interpretować dosłownie rysunki 3 i 4, to są one reprezentacją przestrzeni odcinków postaci \((p-r,p+r) \subseteq \mathbb{R}\) z metryką Hausdorffa; odcinki takie są jednowymiarowym odpowiednikiem kół.
Tutaj należy nadmienić, że odcinki w \(\mathbb{R},\) koła w \(\mathbb{R}^2,\) kule w \(\mathbb{R}^3\) oraz obszary jak te z rysunku 4 obejmujemy wspólną nazwą kul. W każdym z przypadków mamy bowiem do czynienia ze zbiorem wszystkich punktów odległych od zadanego punktu \(\mathbf{p}\) o najwyżej \(r\) – zmianie ulega jedynie sens słów punkt i odległość.
Zanim przejdziemy do ostatniej możliwości, wspomnijmy o tak zwanej odległości euklidesowej: \(d(P,Q) = \sqrt{|\mathbf{p}-\mathbf{q}|^2+|r_1-r_2|^2}\) dla \(P = B(\mathbf{p},r_1),\) \(Q = B(\mathbf{q},r_2).\) Choć różni się ona od odległości Hausdorffa, to są one porównywalne (jedna nigdy nie przekracza dwukrotności drugiej) i obie prowadzą do udzielenia dwóch odpowiedzi \(\diamondsuit\). Geometria związana z odległością euklidesową jest za to dużo bogatsza; z tego też powodu używamy jej na co dzień.
\(\clubsuit\) Slytherin! Najwyraźniej uznajesz, że zastosowanie jednokładności nie zmienia odległości między kołami. Jeśli więc koła \(C,D\) tworzą konfigurację taką jak \(A,B,\) tylko w dwa razy mniejszej skali, to są w tej samej odległości; podobnie mają się \(E,F\) do \(F,G.\) W wielu problemach geometrycznych taki punkt widzenia się opłaca, wszak wszelkie jakościowe zależności – rozłączność, zawieranie, styczność dwóch kół etc. – nie zależą od skali. Jak przekonuje Stephen Semmes, idea ta jest też pożyteczna w analizie matematycznej. Jesteś w dobrym towarzystwie!
Więcej o pożytkach z rozpatrywania odległości niezależnej od skali:
Stephen Semmes, Metric Spaces and Mappings Seen at Many Scales, str. 401–404 załącznika B w:
Michaił Gromow, Metric Structures for Riemannian and Non-Riemannian Spaces, Birkhäuser, 2007.
Interesująca nas metryka nie jest tak łatwa w opisie, ale jak się przekonamy, zawiera w sobie klucz do Komnaty Tajemnic – geometrii hiperbolicznej.
O metryce Ślizgonów.
Żeby ją znaleźć, spróbujmy przeformułować metrykę Hausdorffa w sposób niezmienniczy ze względu na skalowanie: zamiast patrzeć, o ile trzeba powiększyć koło \(P\) dla pokrycia \(Q,\) zbadamy, ilukrotnie trzeba je powiększyć. Jeśli jak poprzednio przyjmiemy \(P = B(\mathbf{p},r_1),\) \(Q = B(\mathbf{q},r_2),\) to tym czynnikiem jest \(\alpha_1 = \frac{|\mathbf{p}-\mathbf{q}|+r_2}{r_1}\); symetrycznie określamy \(\alpha_2\) jako skalę powiększenia \(Q.\) Wydaje się naturalne, że za odległość przyjmuje się większą z liczb \(\alpha_1, \alpha_2,\) ale wynik takiej operacji jest zawsze nie mniejszy od \(1,\) nawet gdy \(P = Q.\) Sytuację można poprawić na różne sposoby, na przykład od \(\max(\alpha_1,\alpha_2)\) odejmując jedynkę, jednak zobaczymy, że najlepiej jest wziąć logarytm (powiedzmy, że naturalny). Prowadzi to do następującej metryki: \[\label{eq:Slytherin} \tag{$\clubsuit$} d(P,Q) = \log \left( \frac{|\mathbf{p}-\mathbf{q}| + \max(r_1,r_2)}{\min(r_1,r_2)} \right) = \log \left( 1 + \frac{|\mathbf{p}-\mathbf{q}| + |r_1-r_2|}{\min(r_1,r_2)} \right).\] Geometria opisana odległością zdefiniowaną wyżej nosi nazwę geometrii hiperbolicznej. W pozostałej części artykułu przyjrzymy się jej bliżej.
Rys. 5. Zaznaczono koła odległe (w metryce opisanej wzorem \(\eqref{eq:Slytherin}\)) od \(P\) o najwyżej \(0{,}4\) oraz te odległe od \(Q\) o najwyżej \(1{,}2\)
Odnotujmy na początek, że \(d(A,B) = \log(3) = d(C,D)\) oraz \(d(E,F) = \log(2) = d(F,G),\) co potwierdza wybór dwóch \(\clubsuit\). Ogólną ilustrację wybranej metryki widzimy na rysunku 5. Nie powinno nas dziwić, że zaznaczone obszary (,,kule”) nie dochodzą do prostej \(r = 0.\) Prosta ta jest ,,nieskończenie daleko” z punktu widzenia naszej metryki. Dlatego też, chociaż modelem przestrzeni kół jest dla nas półprzestrzeń – lub półpłaszczyzna, jeśli badamy przypadek jednowymiarowy – to interesująca nas przestrzeń jest nazywana przestrzenią hiperboliczną, a wymiar niżej – płaszczyzną hiperboliczną. Czytelnikowi polecam samodzielnie poeksperymentować z pomocą komputera i zaobserwować, jakie kształty da się otrzymać, rozważając obszary jak na rysunku 5. Warto też sprawdzić, że spełniona jest nierówność trójkąta (zad. 2).
Rzut oka na geodezyjne.
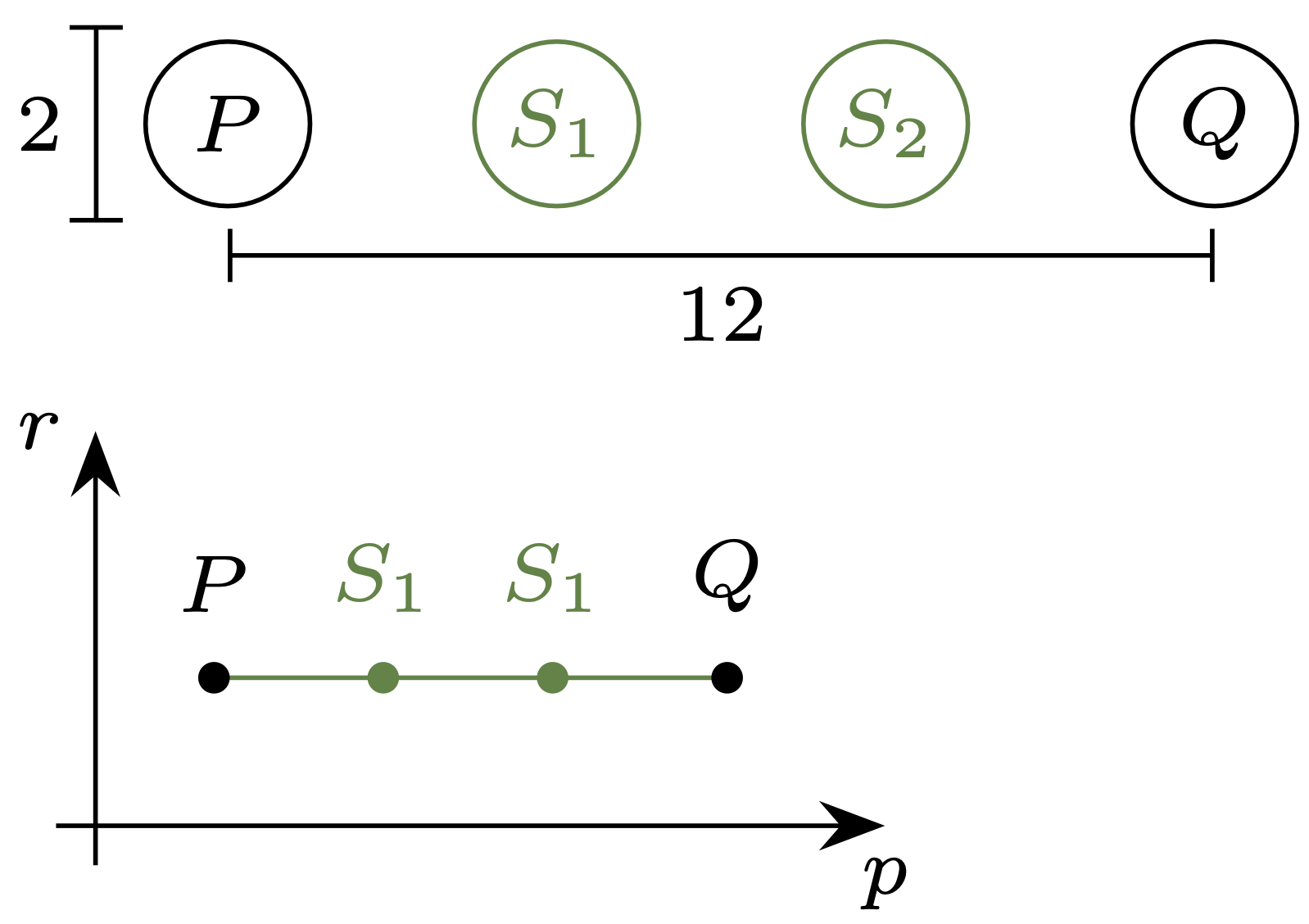
Rozważmy następujący problem: dla kół \(P,Q\) z rysunku 6 (o promieniu \(1\) i środkach odległych o \(12\)) wskazać koła \(S_1,S_2\) w taki sposób, by długość łamanej \([P,S_1,S_2,Q]\) – mierzona jako suma odległości między kolejnymi wierzchołkami łamanej – była najmniejsza. Na rysunku 6 od razu widać narzucające się rozwiązanie: za \(S_1,S_2\) przyjmujemy koła jednostkowe położone w równych odstępach między \(P,Q\); na półpłaszczyźnie ilustrującej przestrzeń kół odpowiada to ,,prostej” łamanej. Jej łączna długość to \(3 \cdot \log(1+4),\) czyli \(\log(125).\)
Zadanie 2. Uzasadnić, że jeśli \(\alpha,\beta \ge 1,\) \(B(\mathbf{p}_1,r_1) \subseteq B(\mathbf{p}_2,\alpha r_2)\) oraz \(B(\mathbf{p}_2,r_2) \subseteq B(\mathbf{p}_3,\beta r_3),\) to \(B(\mathbf{p}_1,r_1) \subseteq B(\mathbf{p}_3,\alpha \beta r_3).\) Wywnioskować, że nierówność trójkąta jest spełniona dla metryki \(\eqref{eq:Slytherin}\).
Rys. 6. Środki kół jednostkowych \(P,Q\) są odległe o \(12.\) Zaproponowana łamana łącząca \(P\) i \(Q\) ma długość \(\log(125)\)
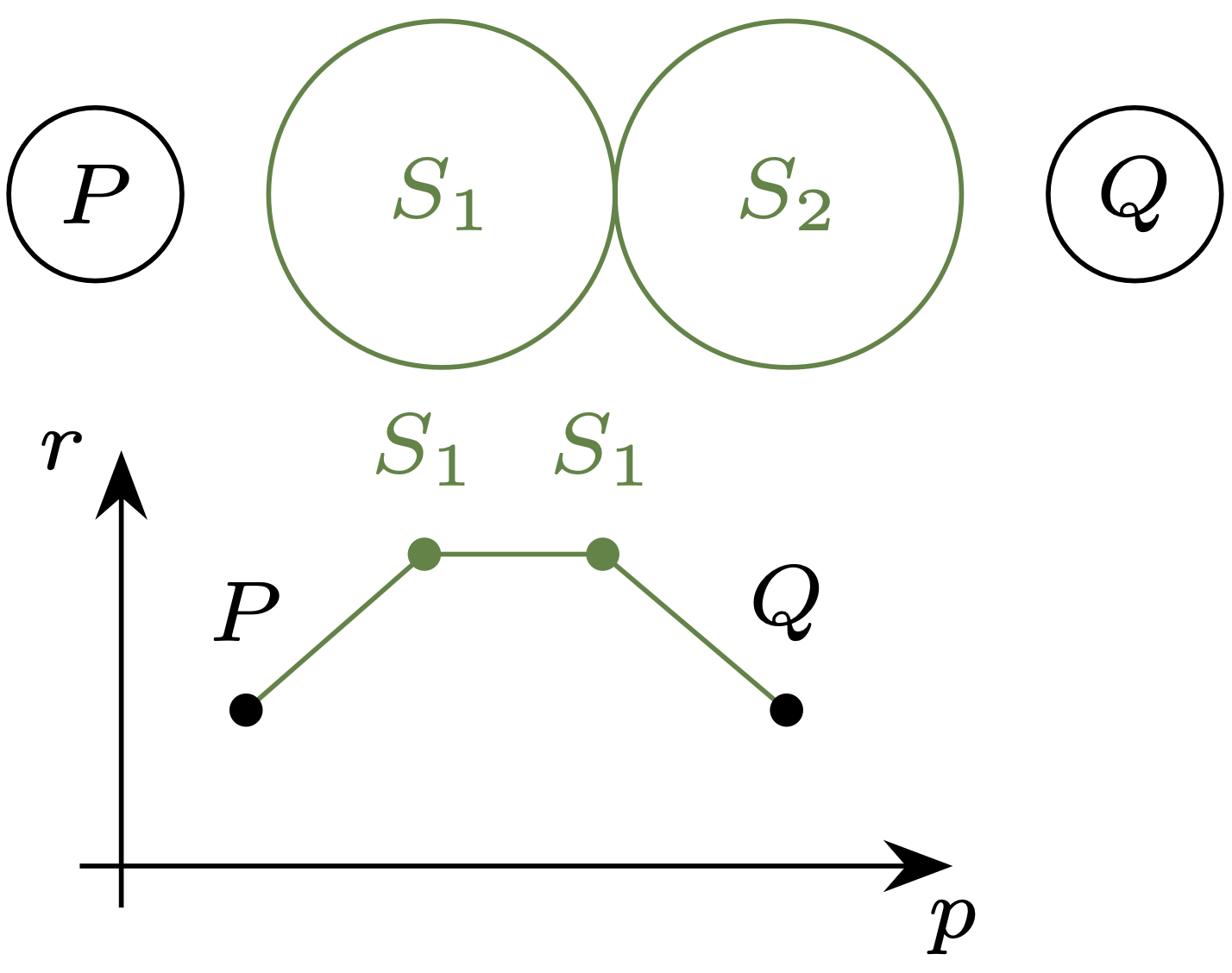
Ale da się lepiej! Optymalnym rozwiązaniem okazują się koła o tych samych środkach, ale promieniu \(2\) (rys. 7). Taka łamana ma długość \({2 \cdot \log(4+2) + \log(\tfrac{4+2}{2})},\) czyli \(\log(108).\) To oczywiście nieznacznie mniej, jednak łatwo znaleźć bardziej jaskrawe przykłady. Gdyby koła \(P,Q\) rozsunąć na odległość \(d > 12,\) to optymalnym rozwiązaniem są koła \(S_1,S_2\) o promieniu \(d/6\) położone w równych odstępach; dla dużych \(d\) daje to łamaną niemal \(\tfrac 32\)-krotnie krótszą niż ta ,,prosta”. Gdybyśmy natomiast nasze zadanie zmienili, każąc szukać łamanej o większej liczbie wierzchołków, to zauważylibyśmy przepaść między rozwiązaniem ,,prostym” a optymalnym.
Rys. 7. Najkrótsza trzyczęściowa łamana łącząca \(P\) i \(Q\) ma długość \(\log(108).\) Wykorzystuje ona koła o tych samych środkach co poprzednio, ale dwukrotnie większym promieniu
Standardowa metryka hiperboliczna.
Jest wiele przykładów pozwalających uzmysłowić sobie różnicę między geometrią euklidesową a hiperboliczną; jeden można znaleźć na marginesie. Większość z nich wymaga jednak bardziej wyrafinowanej metryki niż ta opisana wzorem \(\eqref{eq:Slytherin}\), którą od teraz dla odróżnienia będziemy oznaczać przez \(d_\clubsuit.\)
Przykład. Jeśli ustalimy koło \(X\) i rozważymy wszystkie koła odległe od niego o \(R,\) to da się wśród nich znaleźć (dla dużych \(R\)) około \(e^R\) kół wzajemnie odległych o co najmniej \(1.\) Warto to zestawić z geometrią euklidesową, w której okrąg o promieniu \(R\) ma długość \(2\pi R,\) więc punktów oddzielonych o \(1\) jest jedynie około \(R.\)
Opisaną obok analogię optyczną wymyślił w 1696 roku Johann Bernoulli. Wykorzystał ją do znalezienia kształtu brachistochrony, przyjmując prędkość światła w \((x,y)\) proporcjonalną do \(\sqrt{y}.\) Rozwiązanie to można zobaczyć na kanale 3Blue1Brown na YouTubie:
The Brachistochrone, with Steven Strogatz, youtu.be/Cld0p3a43fU.
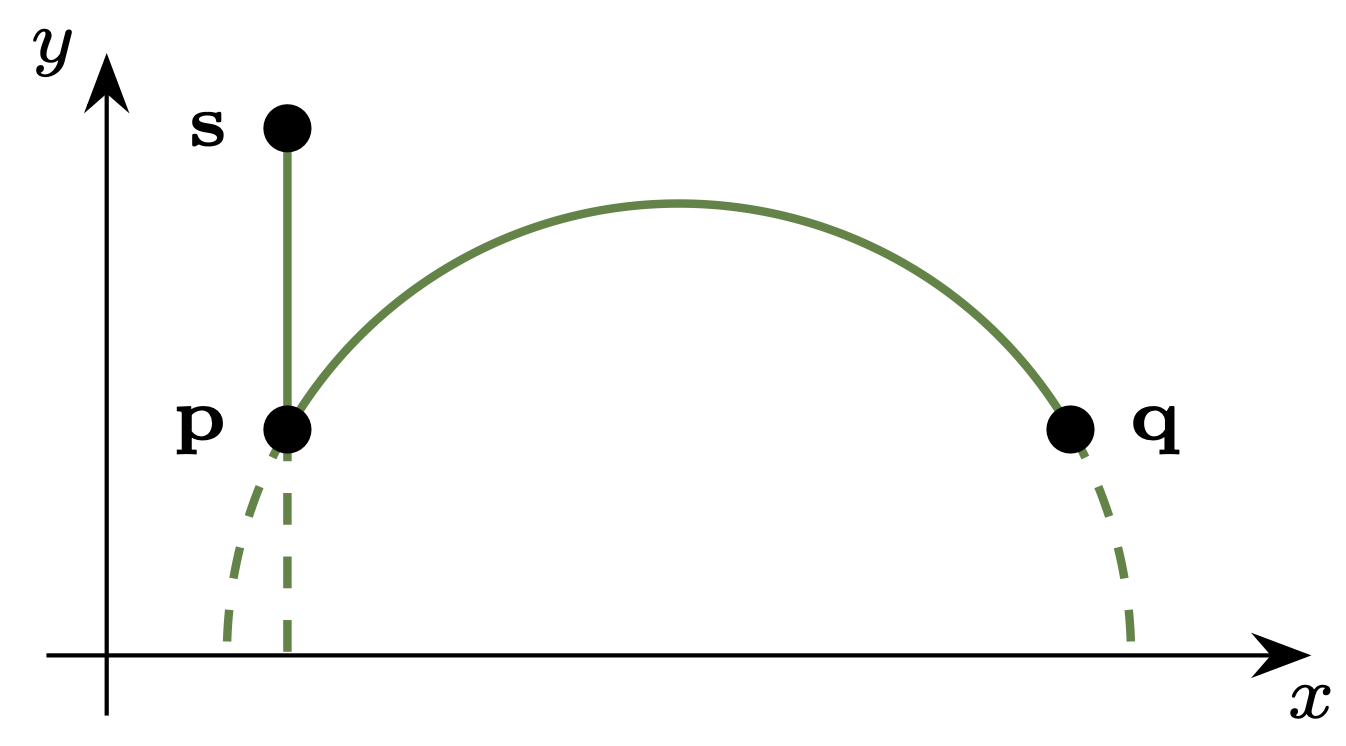
Tę ,,lepszą” metrykę opiszę w oparciu o analogię optyczną. Oderwijmy się od przestrzeni kół i rozważmy światło rozchodzące się w półpłaszczyźnie \(y > 0\) (choć tę samą konstrukcję można powtórzyć w dowolnym wymiarze). Jeśli przyjmiemy, że jego prędkość jest stała i wszędzie wynosi \(1,\) to czas, w którym światło pokonuje daną krzywą, jest po prostu długością tej krzywej. Pokonując drogę z punktu \(\mathbf{p}\) do \(\mathbf{q},\) światło zgodnie z zasadą Fermata ,,wybiera” najszybszą drogę, czyli odcinek łączący te punkty, i zabiera mu to \(|\mathbf{p}-\mathbf{q}|\) czasu – jest to metryka euklidesowa. Wyobraźmy teraz sobie, że półpłaszczyzna \(y > 0\) jest wypełniona niejednorodnym ośrodkiem, a w punkcie \((x,y)\) światło ma prędkość \(y.\) Wtedy najszybsza droga z punktu do punktu, nazywana krzywą geodezyjną, zazwyczaj nie prowadzi po odcinku (rys. 9). Czas potrzebny na dotarcie z \(\mathbf{p}\) do \(\mathbf{q}\) oznaczymy przez \(d_\mathbb{H}(\mathbf{p},\mathbf{q})\) i to jest właśnie standardowa metryka hiperboliczna. Da się ją wyrazić wzorem: \[d_\mathbb{H}(\mathbf{p},\mathbf{q}) = \log \left( \frac{|\mathbf{p}-\overline{\mathbf{q}}| + |\mathbf{p}-\mathbf{q}|}{|\mathbf{p}-\overline{\mathbf{q}}| - |\mathbf{p}-\mathbf{q}|} \right), \ \ \ \text{gdzie } \overline{(x,y)} = (x,-y).\] Do metryki \(d_\clubsuit\) ma się mniej więcej tak, jak metryka euklidesowa ma się do tej danej wzorem \(|x_1-x_2|+|y_1-y_2|.\) Są one porównywalne – wyniki pomiarów \(d_\mathbb{H}\) i \(d_\clubsuit\) różnią się najwyżej dwukrotnie – ale \(d_\mathbb{H}\) ma szereg przewag. Kule w tej metryce – czyli obszary analogiczne do tych z rysunków 4 i 5 – mają gładki kształt, a dokładnie są kołami (rys. 8). Łatwo wykaże to Czytelnik znający okręgi Apoloniusza (zob. Deltoid w \(\Delta^{1}_{13}\)). Krzywe geodezyjne przyjmują kształt pionowych półprostych oraz półokręgów o średnicy leżącej na osi \(x\) (rys. 9) – to z kolei Czytelnik może wyprowadzić z prawa załamania światła. Kształt geodezyjnych nie powinien zaskakiwać, bo światło ,,omija” obszar niższej prędkości. Jednocześnie wyjaśnia on fenomen zakrzywienia optymalnych łamanych, który widzieliśmy wcześniej.
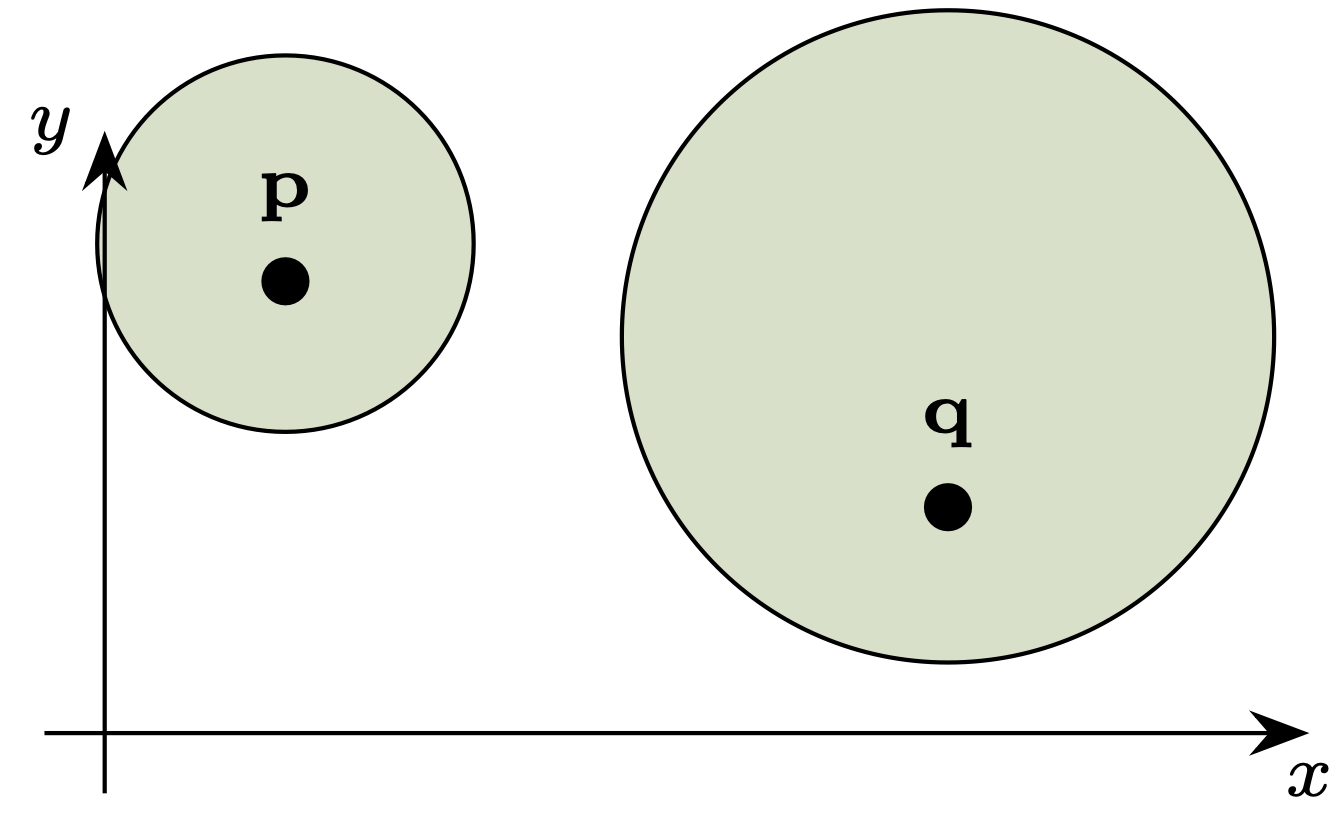
Rys. 8. Kule w metryce \(d_\mathbb{H}\): o środku \(\mathbf{p}\) i promieniu \(0{,}4\); o środku \(\mathbf{q}\) i promieniu \(1{,}2.\) Warto odnotować, że są podobne kształtem i rozmiarem do kul w metryce \(d_\clubsuit\) (rys. 5)
Rys. 9. Krzywe geodezyjne prowadzą z punktu \(\mathbf{p}\) do \(\mathbf{q}\) i \(\mathbf{s}\)
Po wizycie w Komnacie Tajemnic Czytelnik jest dobrze przygotowany, by samodzielnie zgłębiać dalsze tajniki geometrii hiperbolicznej. Oczywiście warto zacząć od Delty – pod hasłami płaszczyzna hiperboliczna czy też Bolyai–Łobaczewskiego – ale możliwe jest też doświadczenie tej geometrii niejako od środka, poprzez gry komputerowe oparte na geometrii hiperbolicznej: HyperRogue i Hyperbolica.