Georg Alexander Pick (1859–1942) był austriackim matematykiem żydowskiego pochodzenia. W latach 1884–1927 pracował na Uniwersytecie Karola w Pradze. Od 1888 roku był profesorem, a od 1889 członkiem Niemieckiej Akademii Nauk Leopoldina. Utrzymywał kontakty z Albertem Einsteinem i Felixem Kleinem. Zajmował się analizą zespoloną, równaniami różniczkowymi, całkowymi oraz geometrią różniczkową. W lipcu 1942 roku został wywieziony do obozu koncentracyjnego Theresienstadt, gdzie zmarł dwa tygodnie później.

Powyższe zdjęcie Georga Picka zostało wykonane ok. 1885 roku
W matematyce Georg Pick znany jest między innymi jako autor pewnego prostego a pięknego twierdzenia dotyczącego kraty, czyli zbioru \({\mathbb{Z}^2=\{(m,n):m,n\in \mathbb{Z}\}}\) na płaszczyźnie euklidesowej \(\mathbb{R}^2.\) Elementy tego zbioru będziemy nazywać punktami kratowymi.
Twierdzenie (G. Pick, 1899). Pole wielokąta \(W,\) którego wierzchołki są punktami kratowymi, a boki nie przecinają się, jest równe \[\vert W\vert =p_w+\frac{1}{2}p_b-1,\] gdzie \(p_w\) jest liczbą punktów kratowych we wnętrzu wielokąta, zaś \(p_b\) liczbą punktów kratowych na jego brzegu.
Dla zaznaczonego wielokąta mamy \(p_w=10\) oraz \(p_b=7,\) zgodnie z twierdzeniem Picka jego pole jest równe \(10+3{,}5-1=12{,}5\)
Oto pomysłowy dowód przez… lanie wody (dosłownie), przedstawiony przez szwajcarskiego matematyka Christiana Blattera w 1997 roku. W każdym punkcie poziomej kraty \(\mathbb{Z}^2\) umieszczamy bryłkę lodu o objętości 1. Bryłki mają kształt cienkich cylindrów (środki podstaw są punktami kratowymi). Następnie czekamy, aż lód się stopi. Woda równomiernie rozleje się na niewsiąkliwej płaszczyźnie, tworząc nieskończony ocean o głębokości 1 (pomijamy parowanie oraz różnice w gęstości wody i lodu). Wtedy objętość wody nad obszarem wielokąta \(W\) jest, co do wartości liczbowej, równa powierzchni wielokąta \(W.\) Ale skąd weźmie się woda nad wielokątem? W trakcie topnienia lodu część wody do niego dopływa, a część wypływa. Zauważmy, że środek dowolnie wybranego boku wielokąta \(W\) jest środkiem symetrii kraty \(\mathbb{Z}^2,\) więc w każdej chwili przepływ wody jest centralnie symetryczny względem tego środka. Zatem całkowity przepływ wody przez tę krawędź wielokąta (więc i każdą inną) jest zerowy. Oznacza to, że ilość wody nad obszarem wielokąta nie zmienia się w czasie! Możemy teraz przyjąć, że bryłki były na tyle cienkie, iż woda nad obszarem wielokąta pochodzi jedynie z bryłek lodu umieszczonych w punktach kratowych we wnętrzu lub na brzegu wielokąta \(W.\) Każdy punkt kraty leżący wewnątrz wielokąta ,,daje” jednostkę wody. Punkt kratowy znajdujący się wewnątrz krawędzi (niebędący jej końcem) ,,daje” pół jednostki wody, a wierzchołek ,,daje” \(\frac{\alpha}{2\pi}\) jednostki wody, gdzie \(\alpha\) jest miarą kąta wewnętrznego wielokąta przy tym wierzchołku. Ponieważ suma miar kątów wewnętrznych \(n\)-kąta \((n\geqslant 3)\) jest równa \((n-2)\pi,\) więc ich całkowity udział zapewnia \(\frac{(n-2)\pi}{2\pi}=\frac{n}{2}-1\) jednostek wody. Stąd teza twierdzenia. \(\Box\)
Christian Blatter, Another Proof of Pick’s Area Theorem, Mathematics Magazine vol. 70, 1997. Sformułowanie autora jest odrobinę inne (mowa w nim o rozchodzeniu się ciepła), pomysł z ,,bryłkami lodu” pochodzi od Güntera M. Zieglera (o czym wspomina przytoczony artykuł).
Wniosek 1. Trójkąt o wierzchołkach w punktach kratowych, który we wnętrzu ani na brzegu nie ma innych punktów kratowych, ma pole równe \(\frac{1}{2}.\)
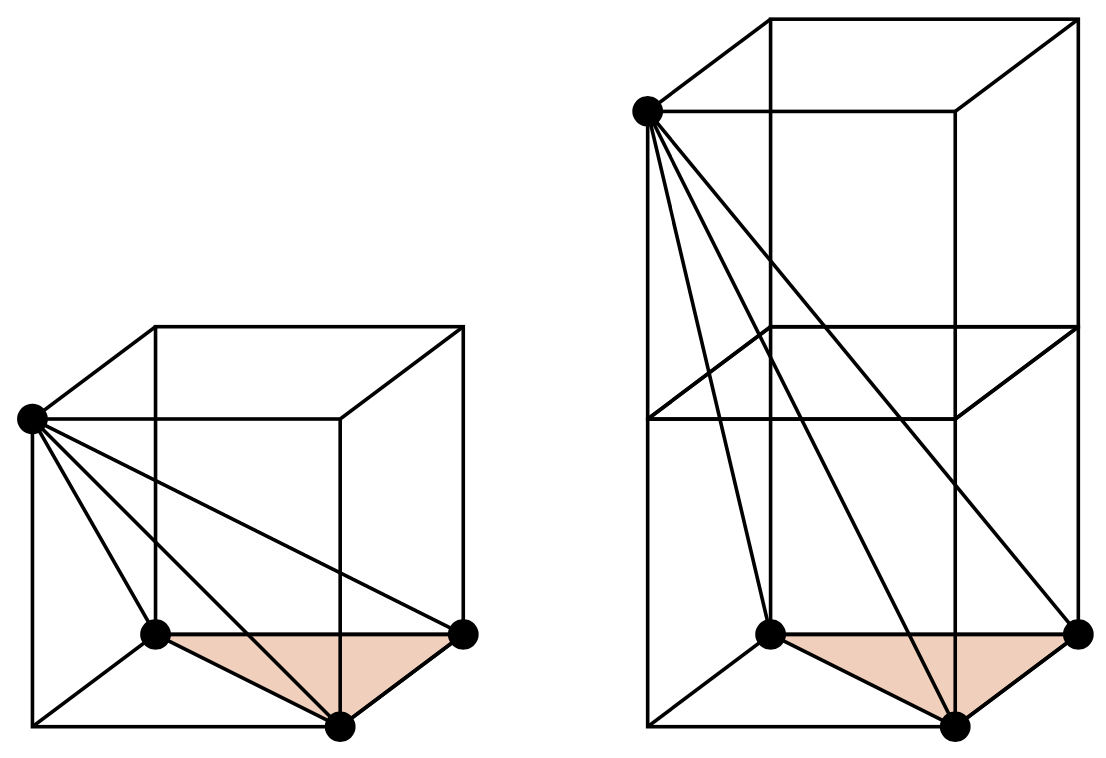
Twierdzenie Picka nie ma rozszerzenia na kratę \(\mathbb{Z}^3.\) Pokazuje to przykład J.E. Reeve’a (1957). Czworościany z rysunku 1 mają 4 wierzchołki w punktach kratowych, nie zawierają innych punktów kratowych, ale mają różne objętości.
Rys. 1
Wykorzystamy teraz powyższy wniosek, aby wykazać podstawową własność tzw. ciągów Fareya.
Przypomnijmy, ciągiem Fareya rzędu \(n\in \mathbb{N}\) (oznaczenie \(f_n\)) nazywamy uporządkowany rosnąco ciąg ułamków nieskracalnych z przedziału \([0,1]\) o mianownikach nie większych od \(n,\) np.: \[\begin{aligned} f_1:&~\bigg\{\frac{0}{1},\frac{1}{1}\bigg\},\ \ \ f_2:~\bigg\{\frac{0}{1},\frac{1}{2},\frac{1}{1}\bigg\},\ \ \ f_3:~\bigg\{\frac{0}{1},\frac{1}{3},\frac{1}{2},\frac{2}{3},\frac{1}{1}\bigg\},\\ f_4:&~\bigg\{\frac{0}{1},\frac{1}{4},\frac{1}{3},\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{1}{1}\bigg\},\ \ \ f_5:~\bigg\{\frac{0}{1},\frac{1}{5},\frac{1}{4},\frac{1}{3},\frac{2}{5},\frac{1}{2},\frac{3}{5},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{1}{1}\bigg\},\\ f_6:&~\bigg\{\frac{0}{1},\frac{1}{6},\frac{1}{5},\frac{1}{4},\frac{1}{3},\frac{2}{5},\frac{1}{2},\frac{3}{5},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6},\frac{1}{1}\bigg\}~\hbox{itd.} \end{aligned}\] Oczywiście \(f_n\subset f_{n+1},\) \(n=1,2,\ldots\)
John Farey (senior) (1766–1826), angielski geolog zainteresowany ,,matematyką dźwięków”, w 1816 roku zadał pytanie: czy dla trzech kolejnych wyrazów ciągu \(f_n\) (\(n\geqslant 2\)), \(\frac{a}{b}<\frac{p}{q}<\frac{c}{d}\) zawsze prawdziwa jest równość \(\frac{p}{q}=\frac{a+c}{b+d}\)? W tym samym roku Augustin-Louis Cauchy (1789–1857) potwierdził – jak pisał – ,,niezwykłą właściwość zwykłych ułamków zaobserwowaną przez pana J. Fareya”.
Ciągi \(f_n\) pojawiły się już w 1802 roku w pracach francuskiego geometry Charlesa Harosa, ale nie wzbudziły wówczas zainteresowania.
Lemat (Cauchy–Farey, 1816). Jeżeli \(\frac{a}{b}<\frac{c}{d}\) są kolejnymi wyrazami ciągu Fareya \(f_n\) \((n\geqslant 1),\) to \(bc-ad=1.\)
Dowód. Punkt \((x,y)\in \mathbb{Z}^2\) nazywamy widzialnym z punktu \((0,0),\) gdy na odcinku łączącym te punkty nie ma innych punktów kratowych.
Jeżeli każdy ułamek \(\frac{a}{b}\in f_n\) utożsamimy z punktem \((b,a)\in \mathbb{Z}^2,\) to punkt \((b,a)\) jest widzialny (bo ułamek \(\frac{a}{b}\) jest nieskracalny) i należy do trójkąta \(T_n\) o wierzchołkach \((0,0),\) \((n,0),\) \((n,n).\) Co więcej, punkt kratowy \((b,a)\in T_n\) jest widzialny wtedy i tylko wtedy, gdy \(\frac{a}{b}\in f_n.\)
Wtedy promień wodzący zaczepiony w punkcie \((0,0)\) i leżący na osi \(OX,\) obracając się przeciwnie do ruchu wskazówek zegara, przechodzi przez kolejne punkty widzialne w trójkącie \(T_n,\) reprezentowane przez ułamki \(\frac{a}{b}\in f_n\) w ich porządku rosnącym. Zatem trójkąt o wierzchołkach \((0,0),\) \((b,a),\) \((d,c)\) nie zawiera innych punktów kratowych, a więc jego pole jest równe \(\frac{1}{2}\) (wniosek 1). Jednocześnie z geometrii analitycznej wiemy, że pole trójkąta, którego wierzchołki mają wyżej dane współrzędne, jest równe \(\frac{1}{2}(bc-ad).\) Stąd \({bc-ad=1}.\) \(\Box\)
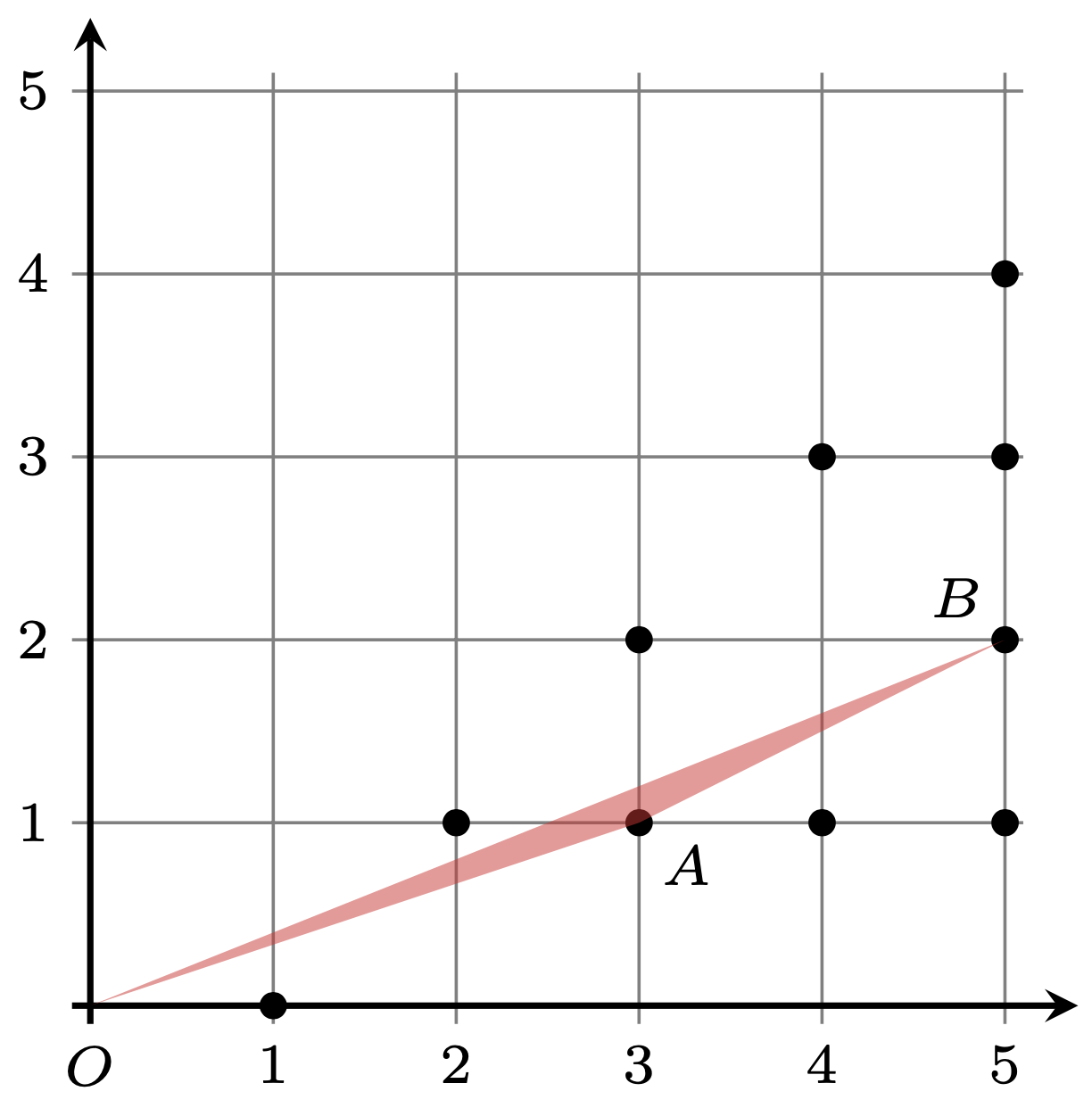
Rys. 2. Zaznaczone punkty odpowiadają wyrazom ciągu \(f_6,\) przy czym \(A=(3,1)\) i \(B=(5,2)\) odpowiadają dwóm kolejnym wyrazom. Wewnątrz trójkąta \(AOB\) nie ma żadnego punktu kratowego, zatem zgodnie ze wzorem Picka jego pole jest równe \(\frac{1}{2}\)
Wniosek 2. Jeżeli \(\frac{a}{b}<\frac{p}{q}<\frac{c}{d}\) są trzema kolejnymi wyrazami ciągu \(f_n,\) \(n\geqslant 2,\) to \(\frac{p}{q}=\frac{a+c}{b+d}.\)
Dowód. Z lematu \(bp-aq=1=qc-pd,\) skąd wynika teza. \(\Box\)
Ciągi Fareya znalazły zastosowanie w aproksymacji liczb niewymiernych liczbami wymiernymi, znamy ich związek z algorytmem (drzewem) Sterna–Brocota, z hipotezą Riemanna czy z ,,problemem \(3n+1\)”. To jest jednak temat na inne spotkanie.
Kraty \(\mathbb{Z}^2\) pojawiły się np. na stronie 6 oraz w \(\Delta_{19}^1\), a ciągi Fareya w \(\Delta_{08}^6\), \(\Delta_{10}^5\).