Wydział Matematyki, Informatyki i Mechaniki UW
Trochę skłamałem w tytule. Z odręcznym narysowaniem stożka radzę sobie całkiem dobrze, o proszę:
Ostatnio jednak na potrzeby ilustracji jednego ze swoich artykułów chciałem wykonać bardziej profesjonalnie wyglądający rysunek. Ponieważ teksty do Delty tworzymy w systemie LaTeX, do rysunków zazwyczaj korzystamy z jego rozszerzenia (pakietu TikZ), które pozwala precyzyjnie rysować za pomocą odpowiednich komend.
Wydało mi się, że zadanie nie jest trudne. Za podstawę stożka można przyjąć elipsę o środku w \((0,0)\) oraz półosiach długości \(2\) i \(1\) – TikZ dobrze sobie z tym radzi, wystarczą polecenia \draw i ellipse. Powierzchnia boczna składa się z tworzących, czyli odcinków łączących punkty podstawy z wierzchołkiem – ten umieśćmy w \((0,3).\) Do wykonania zarysu wystarczą dwie ,,skrajne” tworzące, czyli te poprowadzone do końców wielkiej osi (punktów \((\pm 2, 0)\)) – to również nie jest problem.
Spójrzmy na efekt:
\draw
(0,0) ellipse [x radius = 2, y radius = 1]
(2,0) -- (0,3) -- (-2,0);Od razu widać, gdzie jest problem: narysowałem nie te tworzące, co trzeba! ,,Skrajne” tworzące to te, które są styczne do elipsy, a nie te poprowadzone do końców osi. Natrafiliśmy więc na następujące zadanie: z danego punktu \(V\) poprowadzić styczną do zadanej elipsy \(E.\) Przed dalszą lekturą polecam samodzielnie się nad nim pochylić, a poniżej podam trzy rozwiązania o różnym stopniu przydatności.
Klasyczna konstrukcja stycznej.
Zabierzmy się do tego jak starożytni. Elipsa \(E\) jest wyznaczona przez swoje ogniska \(F,\) \(G\) oraz długość wielkiej osi \(2a,\) mianowicie składa się ze wszystkich punktów \(P\) spełniających \(PF+PG = 2a.\) Styczną do elipsy w punkcie \(P\) można scharakteryzować jako dwusieczną kąta zewnętrznego \(\measuredangle FPG.\) Skonstruujemy teraz styczną poprowadzoną z zadanego punktu \(V\) na zewnątrz elipsy. Gorąco polecam lekturę Deltoidu z \(\Delta^{10}_{10}\) – pozwoli ona szybko zrozumieć, dlaczego konstrukcja, którą zaraz pokażemy, działa.
Narysujmy okrąg o środku \(F\) i promieniu \(2a.\) Na tym okręgu za pomocą cyrkla znajdźmy punkt \(Q\) spełniający \(VQ = VG\) (są dwa takie punkty), a następnie poprowadźmy symetralną \(k\) odcinka \(GQ\) – to jest właśnie szukana styczna. Drugą styczną otrzymamy, zamiast \(Q\) wybierając ten drugi punkt. Punkt styczności \(P\) znajduje się na przecięciu prostej \(k\) z promieniem \(FQ.\) Z równości \[PF + PG = PF + PQ = FQ = 2a\] wnioskujemy, że rzeczywiście leży on na elipsie. Co więcej, \(k\) faktycznie jest dwusieczną kąta \(GPQ,\) co dowodzi poprawności konstrukcji.
O ile konstrukcja ta jest łatwa do wykonania cyrklem i linijką, to trudno ją przepisać w postaci komend TikZ. Poszukajmy więc dalej.
Konstrukcja analityczna.
Gdybym zadanie poprowadzenia stycznej napotkał na maturze, zrobiłbym to tak. Szukana styczna musi przechodzić przez punkt \((0,3),\) więc jest opisana równaniem \(y = ax+3,\) przy czym współczynnik \(a\) nie jest nam znany. Elipsa za to jest znana: jej równanie to \((x/2)^2 + y^2 = 1.\) Punkty przecięcia wyznaczamy, wstawiając jeden wzór do drugiego:
\[(x/2)^2 + (ax+3)^2 = 1.\]
Gdybyśmy znali \(a,\) po prostu to równanie kwadratowe byśmy rozwiązali. I tu jest miejsce na kluczowy pomysł: z góry wiemy, że rozwiązanie ma być tylko jedno, wszak prosta ma być styczna do elipsy. Ta wiedza przekłada się na warunek, że wyróżnik równania jest zerowy. To prowadzi do równania
\[0 = \Delta = (6a)^2 - 4 \cdot (a^2 + \tfrac 14) \cdot 8,\]
z którego wyznaczamy \(a = \pm \sqrt{2}.\) Podstawiając tę wartość do poprzednich równań, otrzymujemy punkty styczności \((\pm \frac{4\sqrt{2}}{3}, \frac 13).\) Dla czytelności kodu wartość \(\frac{4\sqrt{2}}{3}\) przypiszemy osobnej zmiennej \X. Sprawdźmy, czy działa:
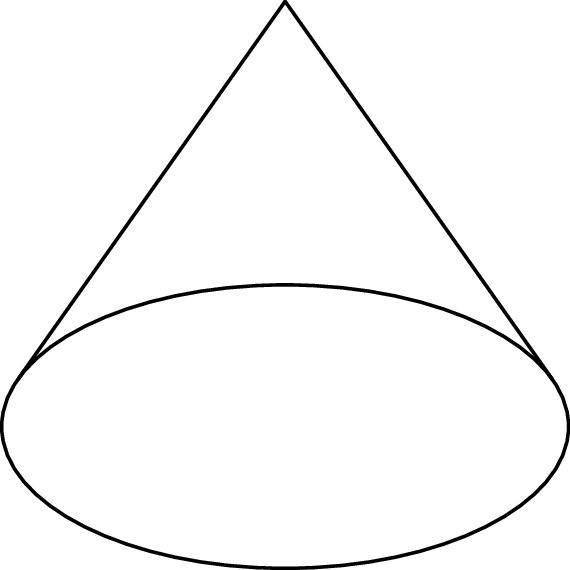
\def \X {{4*sqrt(2)/3}}
\draw
(0,0) ellipse [x radius = 2, y radius = 1]
(\X,1/3) -- (0,3) -- (-\X,1/3);Droga na skróty.
Podzielę się jeszcze jednym rozwiązaniem. Otóż styczną do okręgu jest znacznie łatwiej wyznaczyć niż styczną do innej elipsy:
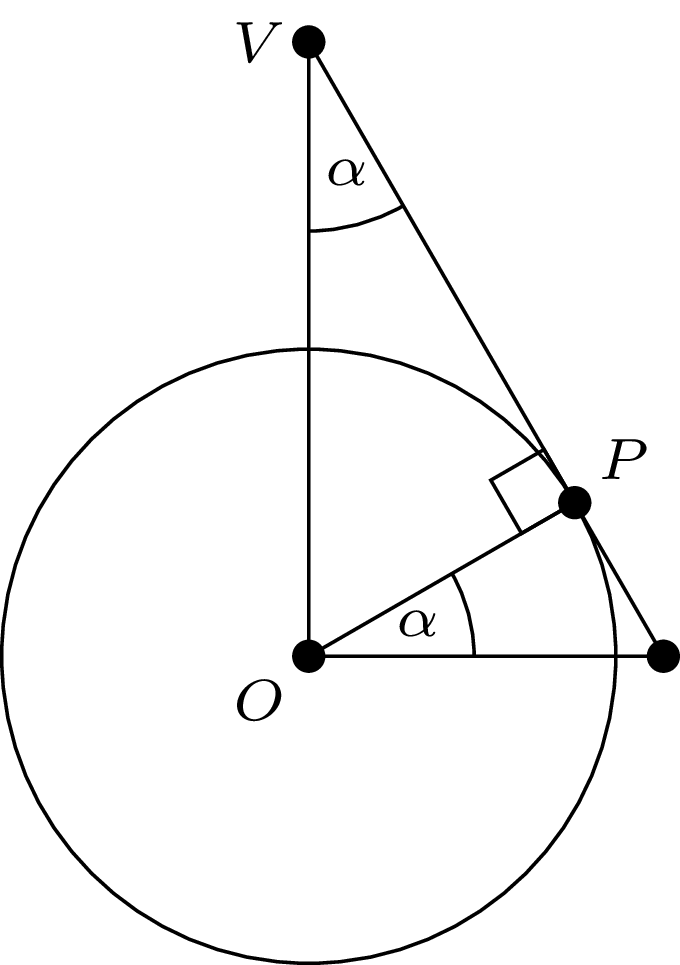Przyjmijmy, że na okręgu jednostkowym wybraliśmy punkt styczności \(P = (\cos \alpha, \sin \alpha),\) co we współrzędnych biegunowych wyraża się po prostu jako \((\alpha:1),\) i szukamy punktu przecięcia \(V\) stycznej z osią \(y.\) Rzut oka na kąty na rysunku mówi nam, że \(V = (0, \frac{1}{\sin \alpha}).\)
Ale do czego ta obserwacja może się przydać? Otóż elipsę o półosiach \(2\) i \(1\) możemy otrzymać, odpowiednio rozciągając okrąg jednostkowy, lub ściślej, dokonując skalowania w osi \(x.\) Przy takim przekształceniu styczna do okręgu przechodzi na styczną do powstałej elipsy. Tak się składa, że TikZ pozwala na dowolne skalowanie obu osi, więc wystarczy naprawdę prosty kod. Oprócz koła jednostkowego rysujemy odcinki z punktu \((0,\frac{1}{\sin \alpha})\) do punktów o współrzędnych biegunowych \((\alpha:1)\) i \((180^\circ-\alpha:1),\) a następnie całość rozciągamy dwukrotnie. Jeśli chcemy otrzymać ten sam rysunek co poprzednio, przyjmujemy \(\alpha = \arcsin(1/3) \approx 19^\circ.\) Voilà:
\draw[xscale=2]
(0,0) circle [radius = 1]
(α:1) -- (0,{1/sin(α)}) -- (180-α:1);Da się lepiej?
Na koniec mam dla Czytelnika pytanie: czy umiesz to zrobić jeszcze prościej? Może znasz narzędzie komputerowe, w którym łatwo jest modelować trójwymiarowy stożek i narysować jego rzut? A może nie warto kombinować? Po prostu narysujmy mniejszy i smuklejszy stożek, używając grubszej kreski! Jak mawiał mój nauczyciel geometrii, ,,każde trzy punkty są współliniowe, jeśli prosta jest wystarczająca gruba”.
\draw[line width=4]
(0,0) ellipse [x radius = 1.5, y radius = 0.6]
(1.5,0) -- (0,3) -- (-1.5,0);