Obroty o pewne szczególne kąty

W kąciku nr 74 ( ${\mathrm{\Delta }}_{25}^2$ ) pisałem o symetrii środkowej, która jest tym samym co obrót o kąt ${180}^{\circ }$ wokół środka symetrii. Tym razem będzie o obrotach o kąty ${90}^{\circ }$ i  ${60}^{\circ }.$ Ogólna zasada stosowania obrotów w rozwiązywaniu zadań jest następująca: obracamy pewną część rysunku w taki sposób, żeby ją dopasować w innym miejscu.

Dla ścisłości – wszystkie figury podajemy tu z kolejnością wierzchołków przeciwną do ruchu wskazówek zegara i również w tym kierunku wykonujemy obroty.

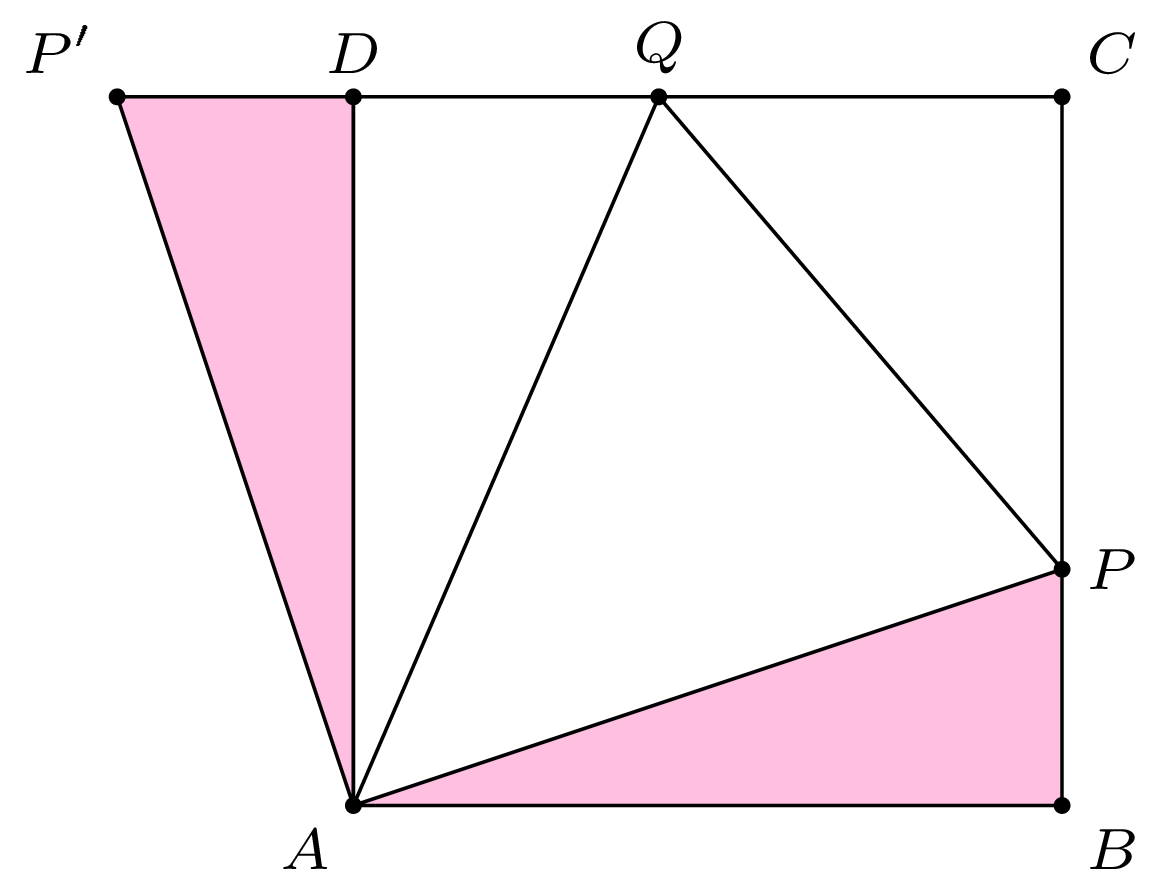
Przykład 1. W kwadracie $ABCD$ punkty $P$ i  $Q$ leżą, odpowiednio, na bokach $BC$ i  $CD,$ przy czym $|\measuredangle PAQ|={45}^{\circ }$ (rys. 1). Udowodnić, że $|BP|+|DQ|=|PQ|.$

Rozwiązanie. Obróćmy trójkąt $ABP$ wokół punktu $A$ o kąt ${90}^{\circ }$ – otrzymamy trójkąt $AD{P}^{\prime }$ przystający do $ABP.$ Zachodzą równości $|\measuredangle ADQ|=|\measuredangle AD{P}^{\prime }|={90}^{\circ },$ więc $|P^{\prime }Q|=|D{P}^{\prime }|+|DQ|=|BP|+|DQ|.$ Z drugiej strony $|PQ|=|P^{\prime }Q|,$ gdyż trójkąty $APQ$ i  $AQ{P}^{\prime }$ są przystające (bkb).

Obrót o ${60}^{\circ }$ można wykorzystać do weryfikacji, czy dany trójkąt jest równoboczny. Trójkąt $XYZ$ jest równoboczny wtedy i tylko wtedy, gdy któryś z punktów $X,$ $Y,$ $Z$ jest obrazem drugiego w obrocie o ${60}^{\circ }$ względem trzeciego. Można sformułować analogiczną zasadę dla równoramienności trójkąta prostokątnego, a nawet dowolnego.

Jeszcze jedna wskazówka ogólna. Jeśli w danej konfiguracji geometrycznej znajdują się dwie przystające figury, to zawsze warto sprawdzić, co nam daje izometria (na przykład obrót) przekształcająca jedną z nich w drugą.

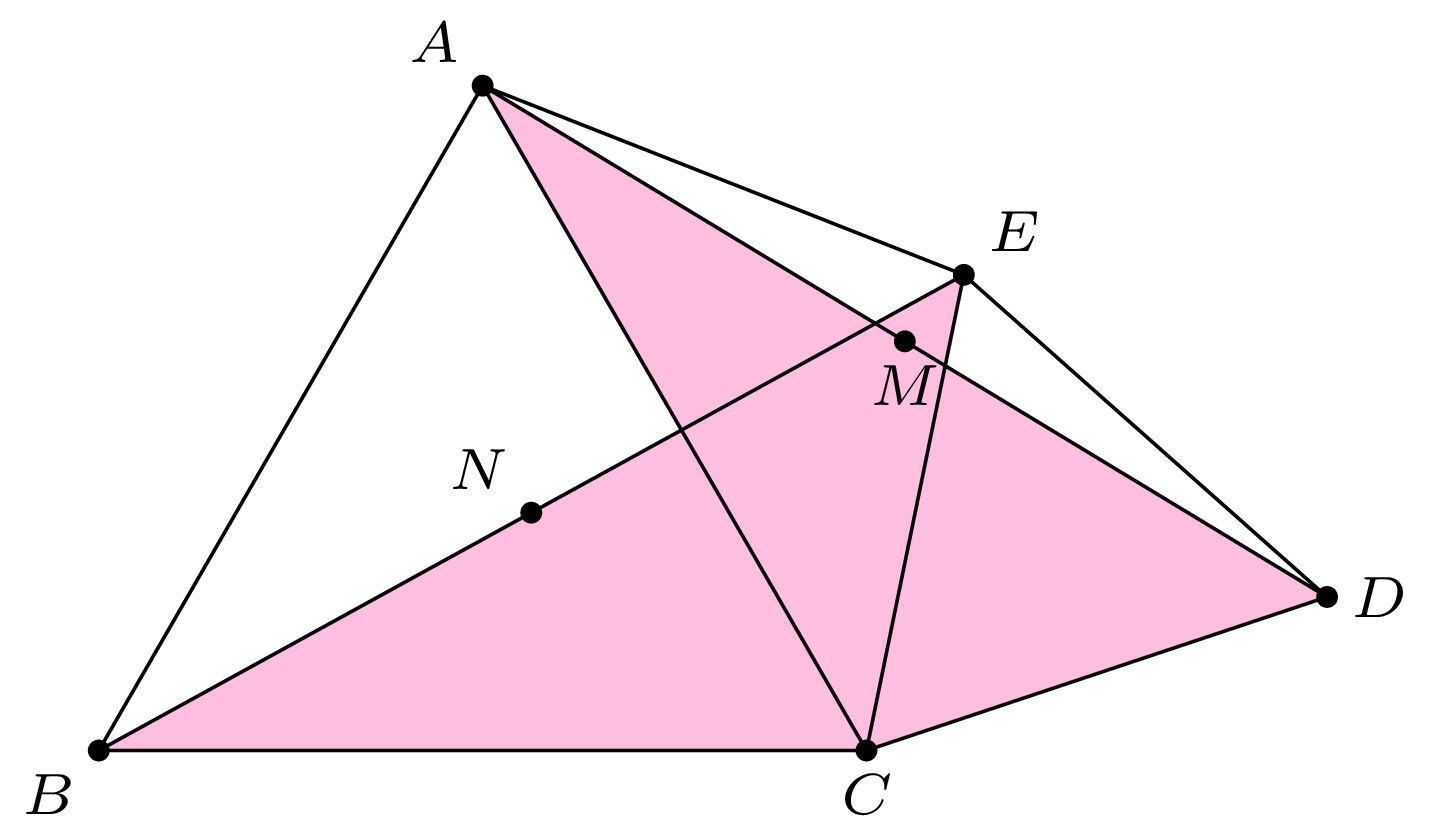
Przykład 2. Dany jest pięciokąt wypukły $ABCDE,$ w którym trójkąty $ABC$ i  $CDE$ są równoboczne. Punkty $M$ i  $N$ są środkami przekątnych, odpowiednio, $AD$ i  $BE$ (rys. 2). Wykazać, że trójkąt $CMN$ jest równoboczny.

Rozwiązanie. Trójkąty $ACD$ i  $BCE$ są przystające (bkb), pierwszy z nich jest obrazem drugiego w obrocie o ${60}^{\circ }$ wokół punktu $C.$ Ten sam obrót przekształca punkt $N$ w punkt $M,$ więc trójkąt $CMN$ jest równoboczny.

Zadania

1. Na bokach trójkąta $ABC$ zbudowano kwadraty $BPQC$ i $CRSA.$ Punkty $K$ i $L$ są środkami odcinków, odpowiednio, $BR$ i $AQ.$ Wykazać, że trójkąt $CKL$ jest prostokątny równoramienny.

   Wskazówka

   Porównaj z przykładem 2.

2. Częścią wspólną kwadratów $ABCD$ i $APQR$ jest punkt $A.$ Punkt $M$ jest środkiem odcinka $DP.$ Udowodnić, że $AM\mathrm{\perp }BR.$

   Wskazówka

   Rozważmy (przystające!) równoległoboki $ADYP$ i $BARX.$ Obrót o ${90}^{\circ }$ wokół środka kwadratu $ABCD$ przeprowadza pierwszy z nich w drugi, więc obrazem prostej $AY$ w tym obrocie jest prosta $BR.$

3. W kwadracie $A_1{A}_2{A}_3{A}_4$ znajduje się punkt $P.$ Prosta ${\ell }_i$ przechodzi przez punkt $A_i$ i jest prostopadła do $A_{i+1}P$ dla $i=1,2,3,4$ (przyjmujemy $A_5=A_1$ ). Udowodnić, że proste ${\ell }_1,$ ${\ell }_2,$ ${\ell }_3,$ ${\ell }_4$ przecinają się w jednym punkcie.

   Wskazówka

   Po obrocie o kąt ${90}^{\circ }$ wokół środka danego kwadratu prosta ${\ell }_i$ przechodzi w prostą $A_{i+1}P.$ Skoro po obrocie wszystkie cztery proste mają punkt wspólny ( $P$ ), to przed obrotem też tak musiało być.

4. W trójkącie $ABC$ dana jest środkowa $CM$ i wysokość $CD.$ Przez dowolny punkt $P$ poprowadzono proste prostopadłe do $AC,$ $BC$ i $MC,$ które przecinają prostą $CD$ w punktach, odpowiednio, $X,$ $Y,$ $N.$ Udowodnić, że punkt $N$ jest środkiem odcinka $XY.$

   Wskazówka

   Przez punkty primowane oznaczmy obrazy w obrocie o ${90}^{\circ }$ punktów z zadania. Trójkąt $X^{\prime }{Y}^{\prime }P$ jest podobny do trójkąta $ABC,$ bo ma odpowiednie boki równoległe do boków tego trójkąta. Prosta $P{N}^{\prime }$ zawiera środkową trójkąta $X^{\prime }{Y}^{\prime }P$ (dlaczego?), więc punkt $N^{\prime }$ jest środkiem odcinka $X^{\prime }{Y}^{\prime }.$

5. Dany jest czworokąt wypukły $ABCD.$ Symetralne odcinków $AB$ i $CD$ przecinają się w punkcie $P,$ przy czym $|\measuredangle APB|=|\measuredangle CPD|={120}^{\circ }.$ Udowodnić, że środki odcinków $AB,$ $BC,$ $CD$ wyznaczają trójkąt równoboczny.

   Wskazówka

   Trójkąt $APC$ po obrocie o ${120}^{\circ }$ przechodzi w trójkąt $BPD,$ więc $|AC|=|BD|$ oraz kąt ostry między nimi ma ${60}^{\circ }.$

6. Udowodnić, że wewnątrz trójkąta równobocznego $ABC$ wszystkie punkty $X$ spełniające równość $|AX{|}^2+|BX{|}^2=|CX{|}^2$ leżą na jednym okręgu.

   Wskazówka

   Niech $X$ będzie punktem spełniającym warunki zadania. Obróćmy trójkąt $ABX$ o ${60}^{\circ }$ wokół punktu $A$ – otrzymamy trójkąt $AC{X}^{\prime }.$ Na mocy twierdzenia Pitagorasa $|\measuredangle C{X}^{\prime }X|={90}^{\circ },$ więc $|\measuredangle AXB|=|\measuredangle A{X}^{\prime }C|={150}^{\circ }.$