Afiliacja: Instytut Matematyki Stosowanej i Mechaniki, Uniwersytet Warszawski
Celem tego artykułu jest przedstawienie, w języku geometrycznej teorii liczb, zagadnienia aproksymacji liczb niewymiernych liczbami wymiernymi, przy użyciu konstrukcji należących do świata starożytnego. Inspiracją dla autora było następujące twierdzenie (podane za [Olds, 2000]).
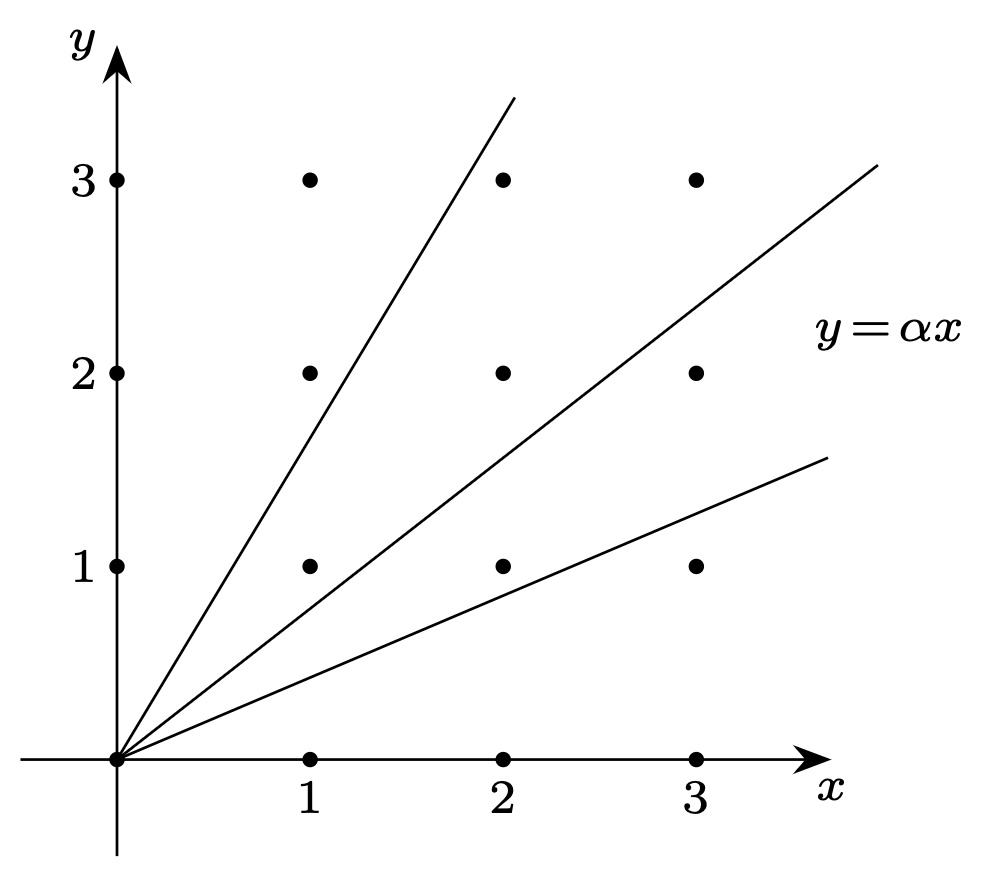
Rys. 1. Proste \(y=\alpha x\) dla różnych liczb niewymiernych \(\alpha>0\) i punkty kratowe. Jedynym punktem kratowym leżącym na tych prostych jest początek układu współrzędnychCzytelnikowi Dociekliwemu proponujemy zbadanie, które z własności (W1)–(W4) sformułowanych w dalszej części artykułu mają swoje uogólnienia na różne od \(\sqrt{2}\) liczby niewymierne.
Twierdzenie 1.1. Każda prosta \(y = ax + b,\) gdzie \(a\) jest liczbą niewymierną, \(b\) zaś jest dowolną liczbą rzeczywistą, ma po obu stronach nieskończenie wiele punktów kratowych leżących bliżej niej niż dowolna przypisana odległość \(\varepsilon> 0,\) bez względu na to, jak małą wartość wybrano dla \(\varepsilon.\)
Pokażemy konstruktywny dowód tego twierdzenia dla \(a=1/\sqrt{2},\) \(b=0,\) przypadku związanego z aproksymacją wymierną liczby \(\sqrt{2}.\) Będzie nas zatem interesowała prosta \(x=\sqrt{2}y\) i liczba \(\sqrt{2},\) którą wybraliśmy z powodu jej ważnego miejsca w historii matematyki, w świetle kryzysu, który wywołała niegdyś w szkole pitagorejskiej. Wybór konkretnej liczby niewymiernej pozwala też na zobaczenie aproksymacji liczbowych i na dalsze eksperymenty numeryczne. Interesują nas liczby, a nie tylko symbole.
Jest oczywiste, że na prostej \(x=\sqrt{2}y\) leży tylko jeden punkt kratowy, którym jest \((0,0).\)
Pokażemy algorytm dający przybliżenia liczby \(\sqrt{2}\) dowolnie blisko z obu stron, jak chce twierdzenie 1.1, i w pewnym sensie najlepszy, a powiązany blisko z jednej strony z algorytmem Herona aproksymacji wymiernej liczby \(\sqrt{2},\) a z drugiej z algorytmem Euklidesa dowodzącym niewymierności tej liczby.
Zauważmy, że np. kolejne ucięcia rozwinięcia dziesiętnego: \[1,\,1{,}4,\, 1{,}41,\, 1{,}414,\, 1{,}4142, \ldots\] liczby \(\sqrt{2}\) zbiegają do niej z dołu oraz bardzo wolno, a metoda Herona daje bardzo szybkie, znakomite przybliżenia, ale niestety tylko z góry, co wkrótce pokażemy.
Rys. 2. Hiperbole \(x^2 - 2y^2 = \pm 1,\) ich asymptoty i punkty kratowe \((1,1),\) \((3,2)\) na nich leżące (punktu \((1,0)\) nie bierzemy pod uwagę)
Wracamy do twierdzenia 1.1 i zapowiadanego konstruktywnego dowodu. Pomysł jest następujący. Rozważmy dwie hiperbole: \[\tag{1}\label{Pell-eq} x^2-2y^2=-1 \ \ \ \text{i} \ \ \ x^2-2y^2=1,\] które będziemy nazywać odpowiednio górną i dolną. Ich asymptotą jest prosta \(x=\sqrt{2}y\) (rys. 2). Jeśli na każdej z hiperbol wskażemy nieskończenie wiele punktów kratowych, to punkty te będą spełniać wymagania twierdzenia 1.1.
Równanie \(\eqref{Pell-eq}\) jest znane jako równanie Pella. Więcej o nim można przeczytać w artykule M. Skałby w \(\Delta^{12}_{21}\).
Zaczniemy od wykazania następującej własności.
(W1) Jeśli punkt kratowy \((p,q)\) leży na górnej lub dolnej hiperboli, to punkt kratowy \((p^2+2q^2,2pq)\) leży na dolnej hiperboli.
Dowód. Ponieważ \((p^2-2q^2)^2 = 1,\) więc ze wzoru skróconego mnożenia \[(p^2+2q^2)^2 -1 =(p^2+2q^2)^2 - (p^2-2q^2)^2 = 2p^2 \cdot 4q^2 = 2(2pq)^2,\] a zatem \((p^2+2q^2)^2 - 2(2pq)^2 = 1,\) co należało wykazać.
Motywacją dla powyższej konstrukcji jest następujący pomysł. Jeśli \({w = \frac pq}\) jest przybliżeniem liczby \(\sqrt{2},\) to \(2/w\) również, tylko z drugiej strony. Spodziewamy się, że średnia arytmetyczna \(\overline{w}\) tych dwóch liczb jest jeszcze lepszym przybliżeniem. Tymczasem: \[\overline{w} = \frac{1}{2} \left( w+\frac{2}{w} \right) = \frac{p^2+2q^2}{2pq}.\] Punkt \((p_1,q_1)=(1,1)\) na górnej hiperboli odpowiada liczbie wymiernej \(\frac{p}{q}=1,\) czyli części całkowitej liczby \(\sqrt{2},\) a dalsze otrzymane w opisany sposób punkty kratowe leżą na dolnej hiperboli i odpowiadają aproksymacji liczby \(\sqrt{2}\) metodą Herona [Krzyżanowski, 2021]. Pierwszymi wyrazami tego ciągu na dolnej hiperboli są liczby \[\tag{2}\label{Heron} \frac{3}{2}, \, \frac{17}{12},\, \frac{577}{408},\, \frac{665857}{470832}, \ldots\] Narzucają się następujące pytania: jak szybko ciąg ten zbiega do swojej granicy?, czy na dolnej hiperboli nie ma innych punktów kratowych? oraz czy nie ma analogicznego algorytmu dającego nieskończony ciąg punktów kratowych na hiperboli górnej?
Na pierwsze pytanie odpowiada następujące oszacowanie.
(W2) Jeśli punkt kratowy \((p,q)\) leży na hiperboli \(x^2-2y^2=1,\) to \(\frac{p}{q}>\sqrt{2}\) oraz \[\tag{3}\label{best} \left| \frac{p}{q}-\sqrt{2} \right| < \frac{1}{2q^2}.\] Dowód. Mamy \(p^2-2q^2 = (p-\sqrt{2}q)(p+\sqrt{2}q) = 1,\) zatem \(p>\sqrt{2}q.\) Ponieważ także \(1 < \sqrt{2},\) więc \[\begin{aligned} 0 & <\frac{p}{q}-\sqrt{2}= \frac{1}{q(p+\sqrt{2}q)} \\&< \frac{\sqrt{2}}{q(2\sqrt{2}q)} = \frac{1}{2q^2}. \ \ \ \text{(Q.E.D.)} \end{aligned}\] Na drugie pytanie odpowiedź jest prosta. Łatwo sprawdzić, że na dolnej hiperboli leży także punkt \((99,70).\) Dalej pokażemy, że takich punktów jest nieskończenie wiele.
Odpowiedź na trzecie pytanie jest twierdząca. Mamy:
(W3) Na górnej hiperboli leży nieskończenie wiele punktów kratowych \((p,q).\)
Dowód. Rozważmy ciąg \((p_n,q_n)\) określony rekurencyjnie: \[\tag{4}\label{rekur} p_{n+1}=p_n+2q_n, \ \ \ q_{n+1}=p_n+q_n.\] Proste rachunki prowadzą do równości \(p_{n+1}^2-2q_{n+1}^2=-(p_n^2-2q_n^2).\) Ponieważ punkt \((p_1,q_1)=(1,1)\) leży na górnej hiperboli, więc punkty o numerach nieparzystych \(3,\) \(5,\) \(7,\) \(\ldots\) także leżą na tej hiperboli. (Q.E.D.)
Tym samym twierdzenie 1.1 dla prostej \(x=\sqrt{2}y\) zostało udowodnione.
Podsumowując: wykazaliśmy, że startując z punktu \((p_1, q_1)=(1,1),\) otrzymaliśmy taki nieskończony ciąg \((p_n,q_n)\) punktów kratowych, że punkty o numerach nieparzystych leżą na hiperboli górnej, punkty o numerach parzystych leżą na hiperboli dolnej.
Jest oczywiste, że ma miejsce nierówność \[\tag{5}\label{both} \frac{p_{2k+1}}{q_{2k+1}}<\sqrt{2}< \frac{p_{2k}}{q_{2k}}\] oraz że ułamki odpowiadające kolejnym punktom na hiperboli górnej tworzą ciąg ściśle rosnący, zbieżny do \(\sqrt{2},\) natomiast ułamki odpowiadające kolejnym punktom na hiperboli dolnej tworzą ciąg ściśle malejący, także zbieżny do \(\sqrt{2}.\) Kolejne wyrazy ciągu przeskakują z jednej hiperboli na drugą. Złożenie dwóch iteracji prowadzi do odwzorowania: \[(p_n,q_n) \longmapsto (3p_n+4q_n, 2p_n+3q_n)= (p_{n+2},q_{n+2}),\] które zastosowane do punktów początkowych \((1,1)\) i \((3,2)\) określa wszystkie kolejne punkty kratowe, odpowiednio, na górnej i dolnej hiperboli. Dowód tego faktu można znaleźć np. w książce [Sierpiński, 1965].
Powracając do oszacowania \(\eqref{best}\) dla aproksymacji wymiernej liczby \(\sqrt{2}\) metodą Herona, można spytać, czy liczbę \(2\) w mianowniku po prawej stronie nierówności można zastąpić większą, aby uzyskać lepsze oszacowanie. Nie chcąc tu, z braku miejsca, wchodzić w subtelności teorii liczb, pokażemy tylko, że liczby \(2\) nie można zastąpić liczbą \(3.\)
(W4) Jeśli \(1<\frac{p}{q}<\frac{3}{2},\) to \(\left| \sqrt{2}-\frac{p}{q} \right| \geq \frac{1}{3q^2}.\)
Dowód. Mamy \(|2q^2-p^2|\geq 1\) i \(\sqrt{2}+\frac{p}{q} \leq 3,\) stąd \[\left| \sqrt{2}-\frac{p}{q} \right| = \frac{|2q^2-p^2|}{q^2(\sqrt{2}+\frac{p}{q})} \geq \frac{1}{3q^2}. \ \ \ \text{(Q.E.D.)}\]
Z zależności \(\eqref{rekur}\) wynika, że \(q_{k+1}p_k -p_{k+1}q_k = p_k^2 -2 q_k^2=(-1)^k,\) a stąd \({\bigl| \frac{p_k}{q_k}-\frac{p_{k+1}}{q_{k+1}} \bigr| \leq \frac{1}{{q_k}q_{k+1}}}.\) Z tej nierówności i nierówności \(\eqref{both}\) otrzymujemy bez trudu oszacowanie \[\left| \sqrt{2}-\frac{p_k}{q_k} \right| < \frac{1}{{q_k}q_{k+1}},\] dla każdej liczby kratowej \((p_k,q_k)\) na dolnej i górnej hiperboli.
Początkowymi wyrazami ciągu określonego rekurencyjnie w \(\eqref{rekur}\) z \((p_1,q_1)=(1,1)\) są \[\tag{6}\label{fraction} \frac{1}{1},\,\frac{3}{2},\, \frac{7}{5},\, \frac{17}{12},\,\frac{41}{29},\, \frac{99}{70},\,\frac{239}{169},\frac{577}{408},\, \frac{1393}{985},\,\frac{3363}{2378},\, \ldots, \frac{665857}{470832}, \, \ldots\] Porównując ten ciąg z ciągiem \(\eqref{Heron}\), widzimy, że ten drugi jest dużo szybciej zbieżny i że gęstość wyrazów ciągu \(\eqref{Heron}\) w ciągu \(\eqref{fraction}\) dąży do zera, gdy \(p_n,q_n\to \infty.\)
Porównajmy szybkość zbieżności aproksymacji dziesiętnych liczby \(\sqrt{2}\) za pomocą ciągu \((1, 1{,}4, 1{,}41, 1{,}414, 1{,}4142, \ldots)\) z szybkością aproksymacji metodą Herona. \(k\)-cyfrowa aproksymacja dziesiętna jest oddalona od liczby \(\sqrt{2}\) o mniej niż \(\frac{1}{10^{k-1}}.\) Natomiast dla aproksymacji Herona mamy: \[\left|\sqrt{2}-\frac{p_n}{q_n} \right| < \frac{1}{2\cdot 10^{2k-2}},\] gdzie \(k\) jest liczbą cyfr liczby \(q_n.\) Wynika to natychmiast z oszacowania \(\eqref{best}\) oraz nierówności \(10^{k-1}\leq q_n\) (porównaj [Apostol, 2002]).
Rys. 3. Geometryczna interpretacja odwzorowania \((x,y) \leftrightarrow (\bar{x},\bar{y})\) \[\begin{cases} \overline{x} = x + 2y \\ \overline{y} = x + y \end{cases}\quad \begin{cases} x = 2\overline{y} - \overline{x} \\ y = \overline{x} - \overline{y} \end{cases}\]
Rekurencja \(\eqref{rekur}\) odegrała fundamentalną rolę w historii matematyki poprzez swoje miejsce w geometrycznym dowodzie niewspółmierności boku kwadratu z jego przekątną. Mianowicie, jeśli skierujemy rekurencję w przeciwną stronę (rys. 3), tzn. \[\tag{7}\label{Pitagoras} x_{n+1}=2y_n-x_n, \ \ \ y_{n+1}=x_n-y_n,\] rozpoczynając od \(x_1=\sqrt{2},\) \(y_1=1,\) liczb reprezentujących długość przekątnej i boku kwadratu, odpowiednio, to otrzymamy ciągi malejące do zera, przy czym stosunek \(x_n/y_n\) jest taki sam dla wszystkich \(n,\) równy \(\sqrt{2}.\) W oryginalnym dowodzie geometrycznym opartym na algorytmie Euklidesa mówi się o długościach przekątnej i boku kwadratu, ich stosunku i podobieństwie konstruowanych kolejno trójkątów (rys. 4).
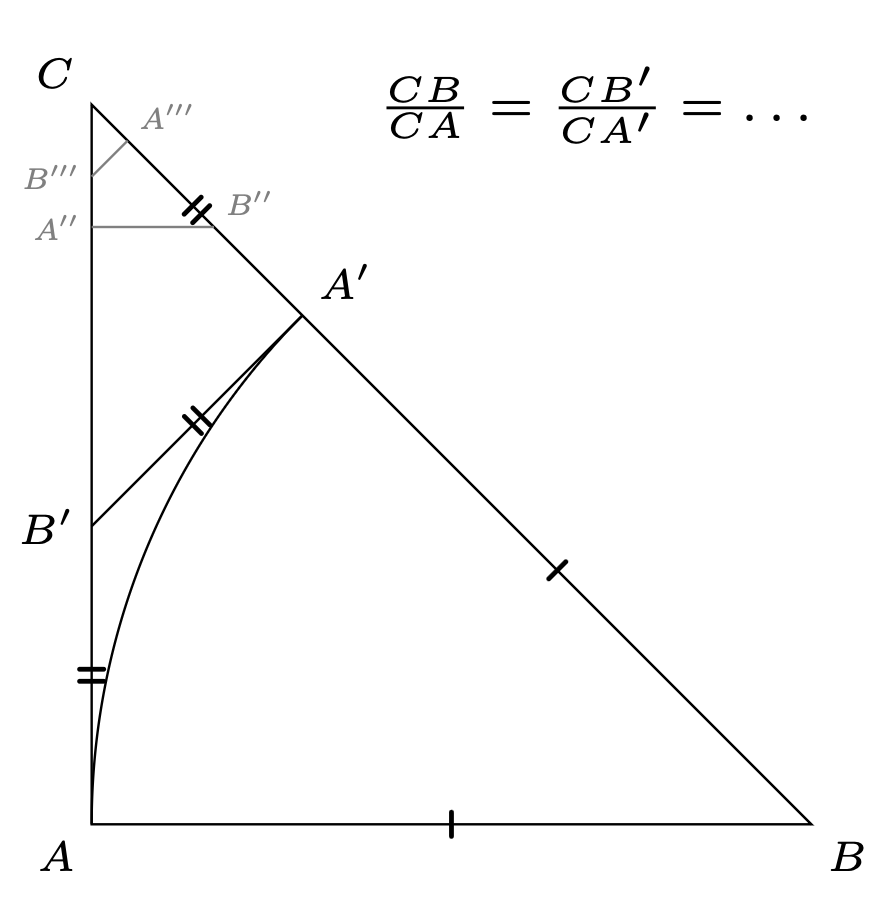
Geometryczny dowód niewspółmierności przekątnej \(CB\) i boku \(CA\) kwadratu jest następujący.
Gdyby istniała wspólna miara \(L,\) to mielibyśmy \(CB=pL,\) \(CA=bL\) dla pewnych liczb naturalnych \(p\) i \(b.\) Stąd: \[B'A = B'A' = CA' = (p-b) L, \ \ \ CB' = CA - B'A = (2b-p)L\] i podobnie \(CB''\) oraz \(CA''\) i wszystkie następne długości przekątnych i boków w konstrukcji miałyby wspólną miarę \(L.\) Ale tak nie może być, bowiem długości tych przekątnych i boków dążą do zera, zatem od pewnego momentu są mniejsze od \(L.\) Otrzymaliśmy sprzeczność, co dowodzi niewspółmierności przekątnej \(CB\) i boku \(CA\) rozważanego kwadratu (patrz [Euklides], Ks. X. Tw. 2).
Rys. 4. Geometryczny dowód niewspółmierności przekątnej \(CB\) i boku \(CA\) kwadratu
Z rysunku 4 odczytujemy następujące relacje: \(CB=CA'+CA\) oraz \({CA=CB'+CA'},\) skąd \(CB=CB'+2CA'.\) Druga i trzecia relacja definiują rekurencje \(\eqref{rekur}\) i \(\eqref{Pitagoras}\). Mamy też: \(\frac{CB}{CA}=\frac{CB'}{CA'},\) skąd \[% \frac{CB}{CA}= 1+\frac{1}{1+\frac{CB}{CA}}.\] Z powyższej równości wnioskujemy, z jednej strony, że \(\frac{CB}{CA}=\sqrt{2},\) a z drugiej, że liczba \(\sqrt{2}\) ma następujące rozwinięcie w nieskończony ułamek łańcuchowy: \(\sqrt{2}=[1;2,2,2,2,2,2,2,\ldots],\) to znaczy \[\sqrt{2}=1+\frac{1}{2+\frac{1}{2 + \ldots}},\] którego redukty \([1;2]=1+\frac{1}{2}={\bf \frac{3}{2}},\) \([1;2,2]=1+\frac{1}{2+\frac{1}{2}}={\bf \frac{7}{5}},\) \([1;2,2,2]={\bf \frac{17}{12}},\) \(\ldots\) są kolejnymi wyrazami ciągu \(\eqref{fraction}\).
Algorytm produkujący kolejne redukty liczby \(\sqrt{2}\) (dający przybliżenia liczby \(\sqrt{2}\) dowolnie blisko z obu stron, jak chce twierdzenie 1.1) jest również w pewnym
sensie najlepszy. Wyjaśniają to następujące własności ułamków łańcuchowych [Chinczyn, 1964]:
(1) Każdy redukt \(p/q\) ułamka łańcuchowego danej liczby niewymiernej \(\alpha\) jest najlepszym możliwym wymiernym przybliżeniem tej liczby o mianowniku nie większym od \(q.\)
(2) Jeśli ułamek nieprzywiedlny spełnia nierówność \(\bigl|\frac{p}{q}-\alpha\bigr| < \frac{1}{2q^2},\) to jest jednym z reduktów ułamka łańcuchowego liczby \(\alpha.\)
Jeśli postawimy pytanie o najlepsze przybliżenie inaczej, pytając o liczbę wymierną o najmniejszym możliwym mianowniku będącą najlepszym przybliżeniem liczby niewymiernej \(\alpha\) z żądaną dokładnością, to niekoniecznie będzie nią redukt ułamka łańcuchowego reprezentującego tę liczbę. Na przykład liczba \(\frac{4}{3}\) nie występuje w ciągu \(\eqref{fraction}\), a jest najlepszym, w powyższym sensie, przybliżeniem wymiernym liczby \(\sqrt{2},\) dla którego \(|\sqrt{2}-\frac{p}{q}|<0{,}081.\) Mamy bowiem \({\bigl|\sqrt{2}-\frac{1}{1}\bigr| >\bigl|\sqrt{2}-\frac{3}{2}\bigr|>0{,}085},\) ale \({\bigl|\sqrt{2}-\frac{4}{3}\bigr| = 0{,}080\ldots < 0{,}081}.\)
Zainteresowanym historią bogatego świata liczb niewymiernych, w szczególności historią zagadnień związanych z ich wymierną aproksymacją, polecamy fascynującą monografię [Havil, 2012].
Bibliografia
[Apostol, Mnatsakanian, 2002] T. Apostol, M. A. Mnatsakanian, Surprisingly Accurate Rational Approximations, Mathematics Magazine, Vol. 75, No. 4 (Oct., 2002), pp. 307-310.
[Euklides] Euclid’s Elements, Book X: http://aleph0.clarku.edu/~djoyce/elements/bookX/propX2.html
[Havil, 2012] J. Havil, Irrationals, Princeton University Press, 2012.
[Chinczyn, 1964] A. Ya. Khinchin, Continued Fractions, The University of Chicago Press, 1964.
[Krzyżanowski, 2021] P. Krzyżanowski, G. Łukaszewicz, Przez wieki z metodą Newtona, \(\Delta^{9}_{21}\).
[Olds, 2000] C. D. Olds, A. Lax, and G. P. Davidoff, Geometry of Numbers, The Mathematical Association of America, 2000.
[Sierpiński, 1965] W. Sierpiński, Wstęp do teorii liczb, Warszawa 1965.