Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Artykuł inspirowany pytaniem zamykającym artykuł Mikołaja Znamierowskiego w \(\Delta^{10}_{25}\).
Czytelnik może pamiętać, że ostatnio już pisałem o pierścieniach Boromeuszy w \(\Delta^8_{25}\). Zapomniałem wtedy jednak zwrócić uwagę na ważny fakt: one nie istnieją!
Rys. 1. Pierścienie Boromeuszy w wersji zbliżonej do tej, jaka pojawia się w herbie tego rodu (F l a n k e r, Wikimedia Commons)
Jak widać na rysunku 1, pierścienie Boromeuszy to konfiguracja trzech okręgów tworzących nietrywialny splot, przy czym po usunięciu dowolnego z nich pozostałe dwa stają się niesplecione. Oczywiście pierścienie nie są okręgami, bo mają swoją grubość – i jak widać na rysunku, różną w różnych miejscach – jednak każdy z pierścieni zawiera w sobie pewien okrąg („rdzeń”), więc możemy sobie pozwolić na takie uproszczenie. Po chwili refleksji łatwo stwierdzić, że okręgi te muszą leżeć w różnych płaszczyznach, inaczej by się przecięły. Czy na pewno więc można znaleźć taką konfigurację w rzeczywistości?
Sprawę utrudnia niestety fakt, że każdy z okręgów na rysunku jest „nad” jednym i „pod” drugim z pozostałych, co uniemożliwia umieszczenie ich w trzech równoległych płaszczyznach, albo też w trzech płaszczyznach odrobinę obróconych względem płaszczyzny rysunku. Przy pewnym wysiłku da się znaleźć odpowiednią konfigurację złożoną z trzech identycznych elips położonych w trzech wzajemnie prostopadłych płaszczyznach (rys. 2). Elipsy te mogą nawet mieć dowolnie mały mimośród, czyli być bardzo podobne do okręgów. Wydaje się, że od znalezienia odpowiednich okręgów dzieli nas niewiele, ale… wcale nie! Przekonamy się o tym, dowodząc następującego, jeszcze mocniejszego stwierdzenia:
Rys. 2. Trzy identyczne prawie-elipsy w trzech wzajemnie prostopadłych płaszczyznach tworzą splot Boromeuszy.
Źródło: C. Gunn, J. Sullivan, The Borromean Rings: A Video about the New IMU Logo, Bridges Leeuwarden: Mathematics, Music, Art, Architecture, Culture, London 2008.
http://archive.bridgesmathart.org/2008/bridges2008-63.html
Twierdzenie (M. Freedman): Jeśli w przestrzeni trójwymiarowej dana jest pewna rodzina okręgów parami niesplątanych, to cała konfiguracja również jest niesplątana.
Jak widać, dopuszczamy, by okręgi miały różne promienie, a nawet, by było ich więcej niż trzy – jak się okaże, ten ogólniejszy przypadek wcale nie wymaga więcej pracy. Jeśli Czytelnik ma za sobą lekturę artykułu Mikołaja Znamierowskiego (str. ), to spodziewa się pewnie, że przedstawię tu dowód wychodzący w czwarty wymiar. I bardzo słusznie! Czwarty wymiar jest niejako wpisany w to twierdzenie jako czas: o braku splątania przekonamy się, podając przepis na rozplątanie, a to oczywiście wymaga czasu. Zanim jednak zwiększymy wymiar, to najpierw go zmniejszymy.
Co jest odpowiednikiem okręgu jeden wymiar niżej? Jeśli ustalimy punkt na osi rzeczywistej (tj. liczbę) \(p \in \mathbb{R}\) i promień \(r > 0,\) to zbiorem punktów odległych od \(p\) o \(r\) jest po prostu para punktów \(\{p-r, p+r\}.\) Podobnie jak okręgi, dwie pary punktów mogą być splątane lub nie (zamiast definicji niech wystarczy tu rys. 3). Przyjmijmy, że mamy daną pewną rodzinę par parami niesplątanych; wskażemy przepis na ich rozplątanie. Każdą z tych (leżących w \(\mathbb{R}\)) par \(\{ p - r, p + r \}\) przedłużmy do (leżącego w \(\mathbb{R}^2\)) okręgu zadanego równaniem \((x-p)^2+t^2 = r^2,\) jak na rysunku 4 – jest to nadal zbiór punktów odległych od \((p,0)\) o \(r,\) tylko w przestrzeni o jeden wymiar większej. Jeśli tylko pary są niesplątane, to odpowiadające im okręgi są rozłączne. Na otrzymanym obrazku przekrój prostą \(t = 0\) daje wyjściowe pary, natomiast przekroje dla większych \(t\) niczym klatki filmu opisują nam, jak każdą z par zdeformować do punktu. Jeśli przyjmiemy przy tym, że pary „znikają” po sklejeniu do punktu, to unikniemy przecięć, czyli nachodzenia jednej pary na drugą. To oczywiście byłoby niemożliwe, gdyby pary były splątane. Zwróćmy uwagę, że ilustracje obok pokazują jedynie dwie pary (i dwa okręgi), ale podany przepis pozwala deformować dowolną liczbę par jednocześnie.
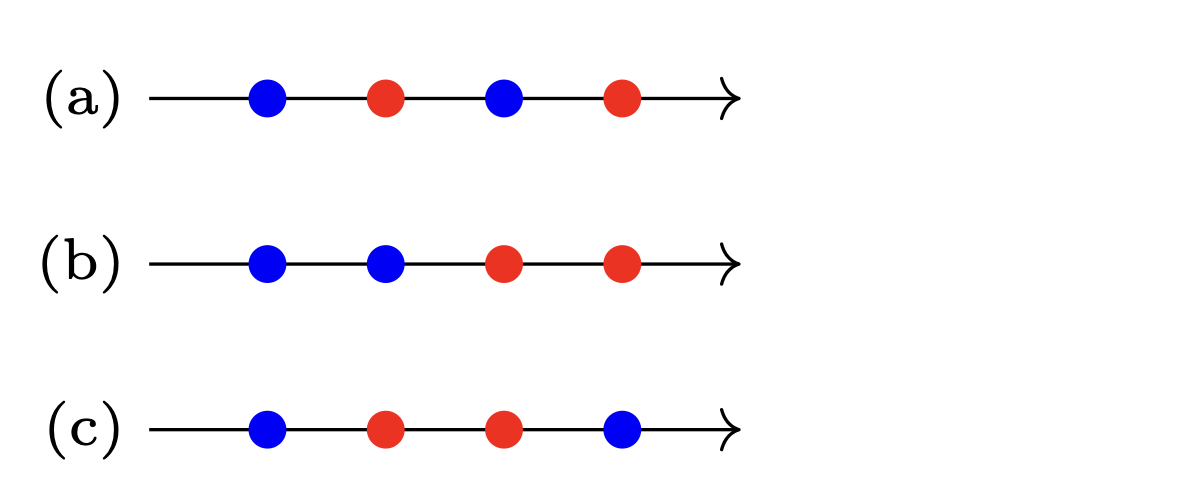
Rys. 3. Pary niebieska i czerwona są:
(a) splątane, (b,c) niesplątane.
Polecam w każdym przypadku dorysować dwa okręgi o średnicach zadanych przez te pary punktów i przekonać się, kiedy okręgi te się przecinają
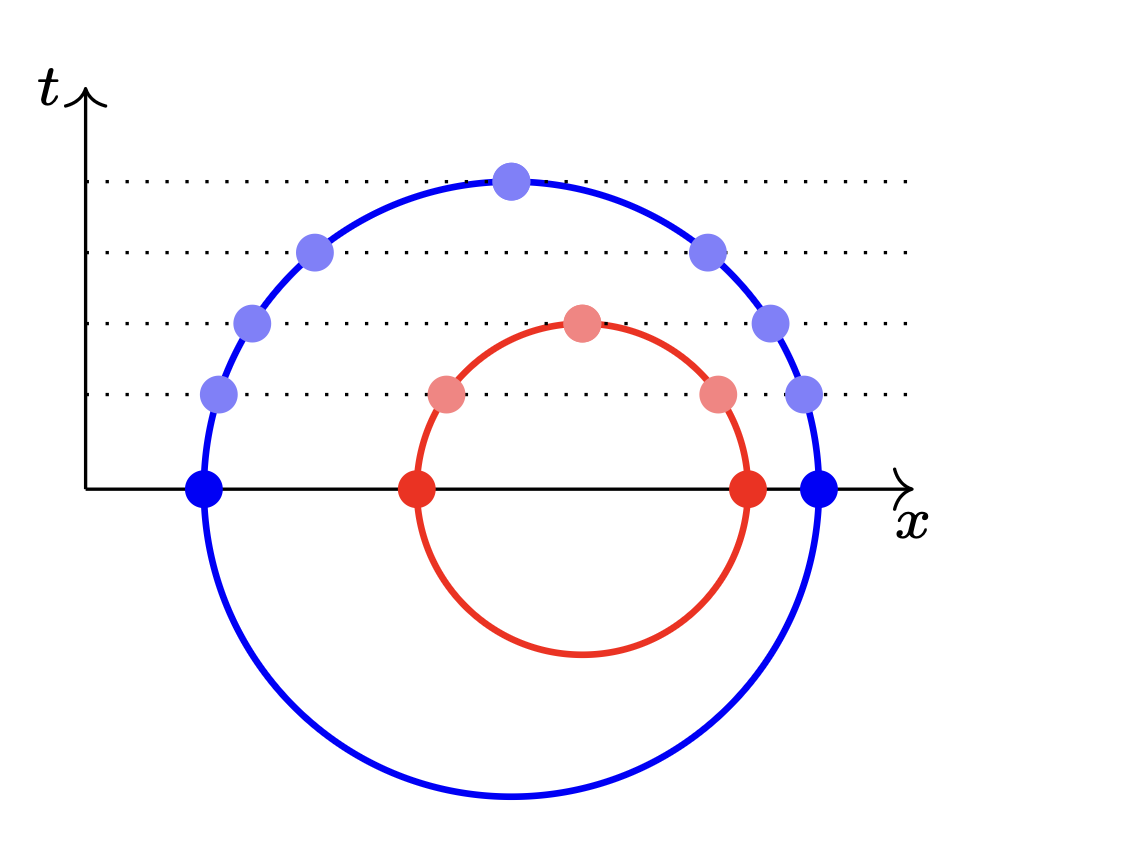
Rys. 4. Dwie niesplątane pary na osi \(x\) (czerwona i niebieska) i odpowiadające im okręgi w płaszczyźnie \(xt.\) Przerywane linie dają przepis na jednoczesną deformację obu par, aż do zniknięcia
Pomysł na dowód Twierdzenia jest podobny, tylko wymaga więcej wyobraźni; żeby się w tym nie zgubić, wprowadźmy oznaczenia. Przyjmijmy, że danych jest \(n\) okręgów \(o_1,\ldots,o_n,\) przy czym \(i\)-ty okrąg ma środek \(p_i = (x_i,y_i,z_i)\) i promień \(r_i,\) a ponadto jest zawarty w płaszczyźnie \(a_i x + b_i y + c_i z = d_i.\)
Do współrzędnych \(x,y,z\) dodajemy teraz czwartą współrzędną \(t\) i każdy z okręgów przedłużamy do sfery w tej większej przestrzeni. Bardziej precyzyjnie, \(S_i \subseteq \mathbb{R}^4\) definiujemy jako zbiór punktów odległych od \((x_i,y_i,z_i,0)\) o \(r_i,\) jednocześnie spełniających to samo równanie co wcześniej. Warto się zastanowić i odnotować – choć wymaga to odrobiny wyobraźni – że w przestrzeni punktów \((x,y,z,t)\) pojedyncze równanie \(a_i x + b_i y + c_i z = d_i\) zadaje podprzestrzeń wymiaru \(3,\) i w tej podprzestrzeni punkty równoodległe od zadanego faktycznie tworzą tradycyjną sferę. W naszej konstrukcji kluczowa jest następująca obserwacja, analogiczna do przypadku jednowymiarowego.
Kluczowa obserwacja: Jeśli okręgi \(o_1,\ldots,o_n \subseteq \mathbb{R}^3\) były niesplątane, to skonstruowane sfery \(S_1,\ldots,S_n \subseteq \mathbb{R}^4\) są rozłączne.
„Kluczowa” nie oznacza, że oczywista. Zanim więc ją uzasadnimy, odetnijmy kupony od jej konsekwencji. Podobnie jak poprzednio, otrzymaną konfigurację możemy ciąć płaszczyznami \(t = \mathrm{const}\) na różnych wysokościach, otrzymując film o okręgach: każdy z nich kurczy się do punktu i znika, unikając kolizji z pozostałymi. Z braku lepszej ilustracji warto znowu spojrzeć na rysunek 4, tym razem w nowym świetle. Zresztą ten film można opisać bez wychodzenia do czwartego wymiaru: okrąg \(o_i\) kurczy się zgodnie ze wzorem na promień \(r(t) = \sqrt{r_i^2 - t^2},\) a po czasie \(r_i\) znika.
Pozostaje techniczny szczegół: przyjęło się, że przy rozplątywaniu okręgów nie należy ich anihilować. Nietrudno to naprawić, bo dzięki rozłączności sfer \(S_i\) nie zdarza się, by dwa okręgi \(o_i\) „znikały” w tym samym punkcie i czasie. Możemy więc na chwilę przed „zniknięciem” \(o_i\) zapauzować film i przesunąć ten tyci okrąg daleko poza scenę, by nie przeszkadzał w dalszym rozwoju wydarzeń (Czytelnik wybaczy mi tutaj skąpość opisu formalnego). W rezultacie po czasie \(\max(r_1,\ldots,r_n)\) widzimy \(n\) małych okręgów umieszczonych daleko od siebie, co rzeczywiście przekonuje nas o tym, że na początku nie mogły być splątane.
Czytelnikom Najwytrwalszym proponuję na deser uzasadnienie „kluczowej obserwacji”. Przypuśćmy, że dwie sfery \(S_i,S_j\) jednak się przecinają, a więc dwa okręgi \(o_i,o_j\) nachodzą na siebie w trakcie ewolucji. Jest to możliwe tylko wtedy, gdy płaszczyzny tych dwóch okręgów zawierają wspólną prostą \(\ell,\) na której ma miejsce kolizja. Prześledźmy więc dokładnie, co się dzieje na tej prostej. Początkowo przecięcia \(o_i \cap \ell,\) \(o_j \cap \ell\) tych okręgów z prostą tworzą dwie pary punktów. Co ważne – niesplątanych, a więc jak na rysunku 3bc! Polecam zastanowić się, dlaczego przecięcia odpowiadające rysunkowi 3a są możliwe tylko w przypadku okręgów splątanych. Czytelnik zapewne już się spodziewa, co dzieje się dalej: te dwie pary podlegają ewolucji jak w przypadku jednowymiarowym. Rzeczywiście, twierdzenie Pitagorasa przekonuje nas, że przecięcie \(S_i\) z płaszczyzną odpowiadającą \(\ell\) (czyli utworzoną przez osie \(\ell\) oraz \(t\)) jest okręgiem – tym samym okręgiem, który rozważalibyśmy w ewolucji jednowymiarowej (jedynie punkt \((x_i,y_i,z_i)\) należy zastąpić jego rzutem na \(\ell\)). Wiemy już, że w jednowymiarowym przypadku kolizja między dwiema parami punktów na \(\ell\) jest niemożliwa, zatem i kolizja między \(o_i\) oraz \(o_j\) tak naprawdę nie może mieć miejsca.
Czy warto było wchodzić w czwarty wymiar? Osądźcie sami.