doktoranci, Wydział Fizyki, Uniwersytet Warszawski
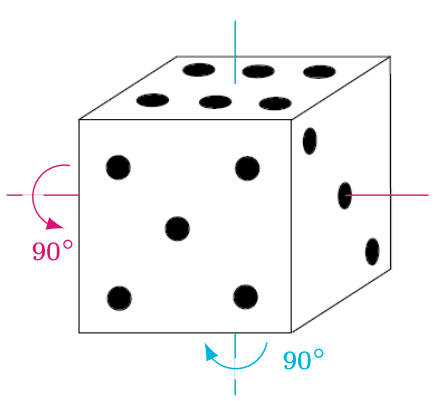
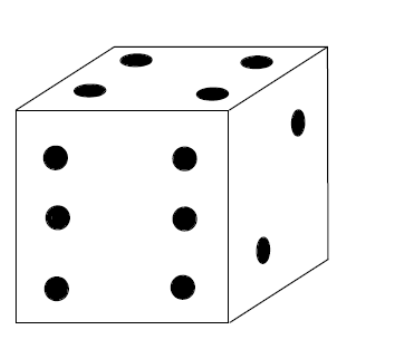
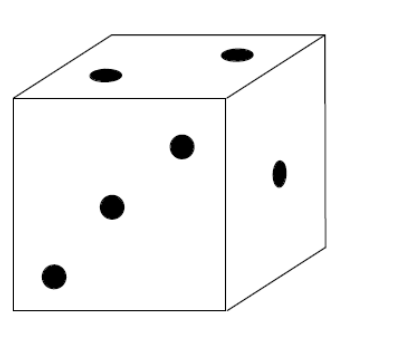
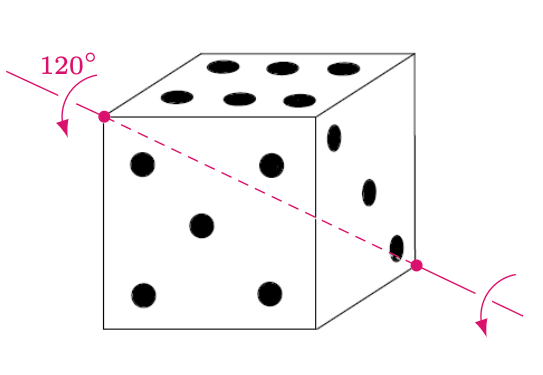
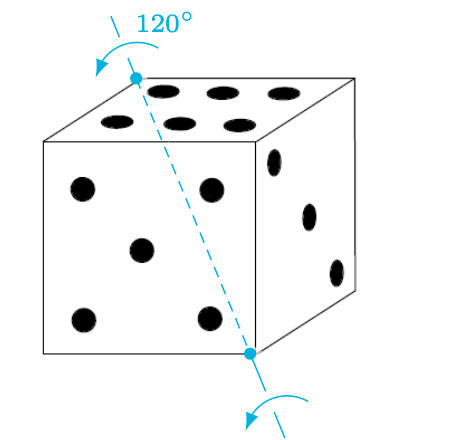
Obroty to bardzo proste zjawiska z życia codziennego, a zarazem niezwykle interesujące obiekty matematyczne. Bardzo dobrze można je „zwizualizować” i zbadać szereg ich własności przy użyciu zwykłej sześciennej kostki. Po pierwsze, obroty kostki są na ogół nieprzemienne, co oznacza, że wykonanie dwóch tych samych ruchów w różnej kolejności prowadzi do różnego stanu końcowego. Dla przykładu wyobraźmy sobie, że na stole leży kostka w położeniu przedstawionym na rysunku 1. Wykonamy zaznaczone ruchy w różnej kolejności, prowadzące do stanów przedstawionych na rysunkach 2 i 3. Co jeszcze ciekawsze, każde takie „podwójne” obrócenie można osiągnąć poprzez pojedynczy obrót, ale wykonany wokół innej osi, co zostało pokazane na rysunkach 4 i 5.
Inną, niezbyt zaskakującą własnością obrotu jest jego odwracalność, która oznacza, że zawsze jesteśmy w stanie wrócić do stanu początkowego, wykonując obrót wokół tej samej osi w przeciwną stronę. Do kompletu wypada dołożyć stwierdzenie, że brak obrotu również jest obrotem, fachowo zwanym identycznością. Powyższe własności obrotów, w języku matematyki, odpowiadają strukturze grupy, a ta konkretna grupa nosi nazwę grupy obrotów, w literaturze oznaczana jako \(SO(3),\) gdzie cyfra 3 odnosi się do wymiaru przestrzeni. Możemy dalej rozważyć zbiór obrotów, które zachowują pewną wybraną płaszczyznę. Takie obroty również tworzą grupę (tym razem przemienną!) \(SO(2),\) a ponieważ są wyodrębnione z większego bytu, określa się je mianem podgrupy, co oznacza, że złożenie dwóch obrotów zachowujących wyróżnioną płaszczyznę również jest takim obrotem. Czytelnik Wtajemniczony powinien wiedzieć, że fakt wyodrębnienia pewnej podgrupy z większej grupy w ogólności wcale nie oznacza, że pozostałe elementy (wraz z identycznością, która jest elementem wspólnym wszystkich podgrup danej grupy) tworzą podgrupę. Ta, wydawałoby się, mało istotna informacja będzie miała kluczowe znaczenie w dalszej części tego artykułu.
Czytelnik Wnikliwy zauważy, że do dopełnienia struktury grupy potrzebna jest jeszcze łączność działania, w tym przypadku składania obrotów.
Żeby zacząć mówić o obrotach w czasoprzestrzeni, trzeba najpierw przybliżyć, czym w zasadzie jest czasoprzestrzeń. Punkty w zwykłej trójwymiarowej przestrzeni scharakteryzowalibyśmy za pomocą trzech liczb opisujących odległość od wybranego przez nas punktu (środka) w trzech prostopadłych kierunkach. Ustalenie tego środka i tych trzech kierunków określa się mianem wyboru układu współrzędnych. Idąc tym tokiem rozumowania, czasoprzestrzeń byłaby zestawem czterech liczb, gdzie jedna z nich (tradycyjnie jest to pierwsza) oznaczałaby upływ czasu od wybranego przez nas momentu, a pozostałe trzy dotyczyłyby przestrzeni. Jednakże czas jest w pewien sposób wyróżniony spośród tych czterech składowych czasoprzestrzennych na skutek stałości prędkości światła. Okazuje się bowiem, że gdy obiekty poruszają się dostatecznie szybko względem naszego układu (np. \(10\%\) wartości prędkości światła, która wynosi \({c=299\, 792\, 458}\) m/s), to odczuwany przez nie upływ czasu oraz mierzone długości różnią się względem tego, co my mierzymy. Dokładniej rzecz ujmując, obiekty (spoczywające w naszym układzie) mierzone w układzie poruszającym się (względem nas) ulegają skróceniu Lorentza, natomiast czas dla obserwatorów ruchomych płynie wolniej (względem naszego układu), i jest to tzw. dylatacja czasu. Takie „niecodzienne” właściwości skutkują powstawaniem wielu ciekawych „paradoksów”. Ich badaniem zajmuje się szczególna teoria względności, która zagościła w świecie fizyki dzięki Albertowi Einsteinowi.
Oczywiście są to paradoksy pozorne, wynikające z tego, że na co dzień nie doświadczamy efektów relatywistycznych i nasza „intuicja” zawodzi. W celu pogłębienia wiedzy odsyłamy do innych artykułów Delty: „Paradoks Roberta Korzeniowskiego” i „Geometria na wirującej karuzeli” Andrzeja Dragana lub „Na czym polega paradoks bliźniąt” Piotra Zalewskiego.
Aby zobaczyć świat oczami innego obserwatora, potrzebna jest stosowna formuła opisująca przejście z jednego układu do drugiego, tzw. transformacja. Jak już wiemy, obserwatorzy spoczywający względem siebie, ale patrzący w różne strony (czyli tacy, którzy wybrali różne kierunki) różnią się względem siebie o obrót, co sugeruje nam, że grupa obrotów należy do zbioru transformacji czasoprzestrzeni, bo przecież otaczający nas świat nie uległ zmianie, a jedynie sposób, w jaki na niego patrzymy. Natomiast żeby opisać przejście pomiędzy obserwatorami, którzy patrzą w tę samą stronę, ale poruszają się względem siebie, potrzebna jest tzw. transformacja Lorentza, nazywana też boostem, dzięki której można analizować i tłumaczyć wspomniane wcześniej „paradoksy”. Co bardzo ważne, ta transformacja w przypadku małych prędkości (względem prędkości światła) jest praktycznie nieodróżnialna od używanej na co dzień i zgodnej z naszą intuicją transformacji Galileusza, według której: jeśli stoimy na peronie i mija nas pociąg z prędkością \(V,\) to względem pasażera tegoż pociągu to peron „odjeżdża” w przeciwną stronę, również z prędkością \(V,\) podczas gdy upływ czasu dla obu obserwatorów jest jednakowy. Zbiór wszystkich tych transformacji czasoprzestrzeni określa się mianem grupy Lorentza – pełni ona niezwykle istotną rolę we współczesnej fizyce i matematyce, i to własności tej grupy odgrywają kluczową rolę w dalszej części tego artykułu.
Na określenie przekształcenia Lorentza zmieniającego prędkości używa się też (zgodnie z zaleceniami Polskiego Towarzystwa Fizycznego) słów pchnięcie albo poryw, zamiast obco brzmiącego słowa boost.
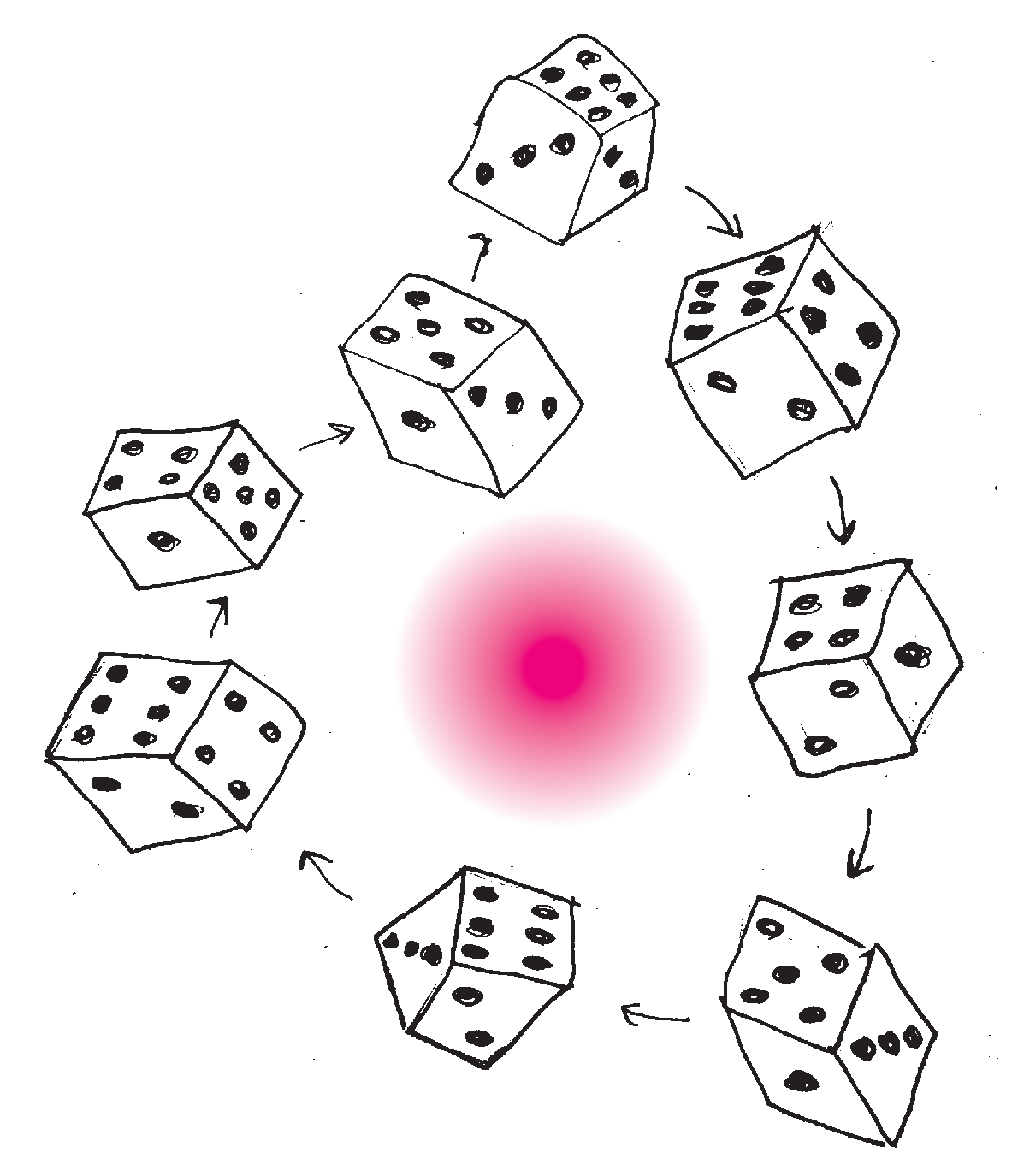
Pokrótce omówiliśmy już sześcienną kostkę, grupę obrotów i kilka interesujących nas własności czasoprzestrzeni, więc teraz przejdziemy do precesji Thomasa. Efekt ten można opisać w następujący sposób: gdy jakiś obiekt porusza się z prędkością relatywistyczną (porównywalną z prędkością światła \(c\)) i kierunek tej prędkości ulegnie zmianie, to ciało (względem nieruchomego obserwatora) obróci się w płaszczyźnie, w której dokonała się zmiana prędkości. Oryginalnie efekt ten dotyczył precesji spinu elektronu (czyli zmiany kierunku wewnętrznego momentu pędu) podczas ruchu orbitalnego wokół jądra atomu. Upraszczając, wyobraźmy sobie, że elektron jest malutką, doskonałą kulką, do której przyczepiona jest strzałka (symbolizująca spin). W trakcie ruchu jednostajnego po okręgu kierunek strzałki będzie się obracał ze stałą prędkością kątową, co przedstawia rysunek 6.
Rys. 6. Precesja spinu elektronu poruszającego się przeciwnie do ruchu wskazówek zegara
Powyższe zjawisko wynika z drugiego (aczkolwiek bardziej elementarnego) tytułowego efektu, mianowicie obrotu Wignera, nad którym się teraz pochylimy. Można go przedstawić w następujący sposób: względem spoczywającego laboratorium porusza się dwóch podróżników: jeden na wschód z prędkością \(v_W,\) a drugi na północ z prędkością \(v_P,\) i każdy z nich ma osie swojego układu współrzędnych ustawione zgodnie ze swoimi kierunkami ruchu. Otóż według podróżnika udającego się na wschód ten poruszający się na północ jest obrócony względem pozycji zarejestrowanej przez laboratorium! Jest to dość zaskakująca obserwacja, ale dlaczego w ogóle ma ona miejsce? Co jest przyczyną takiego efektu? Spróbujemy na to odpowiedzieć w dwójnasób: od strony fizyki oraz matematyki (oczywiście oba te obrazy są spójne i kompatybilne, natomiast argumenty dotykają nieco różnych aspektów).
Z punktu widzenia fizyki kluczowe jest to, że skrócenie Lorentza występuje wyłącznie w kierunku ruchu obserwatora, podczas gdy pomiary w kierunkach prostopadłych nie ulegają zmianie. Krótko mówiąc, jadąc z prędkością \(v\) przez most o długości \(L,\) stwierdzimy, że jest on krótszy niż wskazywałaby na to mapa, bo uzyskalibyśmy wynik \(L\sqrt{1-v^2/c^2},\) natomiast jest tak samo szeroki. Jeśli dołożymy do tego fakt, że względem podróżnika jadącego na wschód podróżnik jadący na północ porusza się pod kątem rozwartym względem wschodniego kierunku, co samo w sobie nie jest efektem relatywistycznym, dostajemy egzotyczną kombinację różnych nieprostopadłych kierunków i częściowych skróceń Lorentza oraz oczywiście dylatacji czasu. Złożenie tych wszystkich efektów daje obrót o kąt \(\phi\) spełniający następujące tożsamości: \[\begin{aligned} \tan \phi = \frac{\frac{v_W v_P}{c^2}}{\sqrt{1-\frac{v_W^2}{c^2}}+\sqrt{1-\frac{v_P^2}{c^2}}} , \ \ \ \sin \phi = \frac{\frac{v_W v_P}{c^2}}{1+\sqrt{1-\frac{v_W^2}{c^2}} \sqrt{1-\frac{v_P^2}{c^2}}}. \end{aligned}\] Matematycznie sprawa jest dużo prostsza: jak już wspomnieliśmy, obroty tworzą podgrupę grupy Lorentza, natomiast boosty już nie. Wynika stąd, że złożenie dwóch dowolnych boostów wcale nie musi być boostem. Powstaje więc pytanie: czym jest takie złożenie? Odpowiedź jest dość prosta: złożeniem obrotu i boostu, dwóch nietrywialnych cegiełek grupy Lorentza.
Miara kąta rozwarcia \(\alpha\) wynika z relatywistycznego składania prędkości i jest zadana warunkiem \(\tan \alpha = - \frac{v_P}{v_W} \sqrt{1-\frac{v_W^2}{c^2}},\) a w przypadku nierelatywistycznym \(\tan \alpha = - \frac{v_P}{v_W} .\)
W ogólności, jeżeli mamy co najmniej dwa wymiary przestrzenne, to boosty nie tworzą podgrupy, natomiast boosty wzdłuż tego samego kierunku przestrzennego już tworzą grupę, i to przemienną.
A jak to się ma do oryginalnego problemu precesji spinu elektronu? Otóż kluczowy jest ruch po okręgu, który co prawda zachowuje długość wektora prędkości, ale nieustannie zmienia jego kierunek! W związku z tym w każdej chwili czasu naszemu elektronowi trzeba przyporządkować nowy układ współrzędnych (tzw. układ chwilowo współporuszający się), co oznacza, że w każdej chwili czasu potrzebny jest obrót, by uczynić zadość transformacji Lorentza, spójności grupy Lorentza i tym samym szczególnej teorii względności. Dla zaspokojenia ciekawości podajemy ogólny wzór na tę częstość: \[\begin{aligned} \vec{\Omega} = \frac{1}{{v}^2}\biggl(\frac{1}{\sqrt{1-{v}^2/c^2}}-1\biggr) \vec{a}\times \vec{v} , \end{aligned}\] gdzie \(\vec{a}\) oznacza przyspieszenie, jakiego doznaje ciało. W przypadku elektronu na orbicie \(\vec{a}\) jest przyspieszeniem dośrodkowym, wobec czego zachodzi następująca równość: \[\begin{aligned} \vec{\Omega} = - \vec{\omega} \biggl(\frac{1}{\sqrt{1-{v}^2/c^2}}-1\biggr) , \label{wz} \end{aligned}\] gdzie \(\vec{\omega}\) oznacza prędkość kątową elektronu. Z powyższego wzoru wynika również, że precesja spinu odbywa się w kierunku przeciwnym do ruchu obiegowego elektronu. Wracając jeszcze na chwilę do rysunku 6, widzimy, że częstość precesji Thomasa \(\Omega\) jest dwukrotnie mniejsza niż prędkość kątowa elektronu \(\omega,\) bo w trakcie pełnego obiegu strzałka obróciła się o 180\(^\circ,\) co pozwala wyznaczyć prędkość elektronu \({v}=\frac{\sqrt{5}}3 c.\)
Czytelników spragnionych wyzwań i rachunków zapraszamy do lektury załącznika (umieszczonego na stronie czasopisma), gdzie przedstawione są dokładne rachunki uzasadniające umieszczone w tym artykule rezultaty.