Kontakt:
gornicki59@gmail.com
Znany już w starożytności problem izoperymetryczny: \[\hbox{\textit{Który z~trójkątów o~ustalonym obwodzie ma największe pole?}}\] rozwiążemy elementarnie, korzystając z nierówności między średnimi.
Przypomnijmy, że średnia geometryczna dodatnich liczb jest nie większa niż ich średnia arytmetyczna. Dla trzech dodatnich liczb \(x,y,z\) stwierdzenie to przybiera postać: \[\root 3\of{xyz}\leqslant\frac{1}{3}(x+y+z),\] więc jeśli \(x+y+z=d,\) to iloczyn \(xyz\) ma wartość największą, gdy \({x=y=z=\frac{1}{3}d},\) bo wtedy \(xyz=(\frac{1}{3}d)^3=[\frac{1}{3}(x+y+z)]^3.\)
Czytelników, którzy nie znają dowodu tego faktu, zachęcamy do wykazania go, szczególnie w używanym w tym artykule przypadku trzech liczb.
Pole trójkąta o bokach długości \(a,b,c\) można łatwo obliczyć, korzystając ze znanego już od I wieku wzoru Herona: \[S=\sqrt{p(p-a)(p-b)(p-c)},~\hbox{gdzie}~p=\frac{1}{2}(a+b+c),\] dlatego przy ustalonym obwodzie \(a + b + c\) wartość \(S\) jest największa, gdy \(p-a=p-b=p-c,\) czyli gdy \(a=b=c.\)
Wykazaliśmy więc twierdzenie:
Twierdzenie 1. Trójkąt o danym obwodzie ma największe pole, gdy jest równoboczny.
Prawdziwy jest fakt ogólniejszy (znany już w starożytnej Grecji):
Twierdzenie 2 (Zenodor, III/II w. p.n.e.). Wielokąt o ustalonym obwodzie ma największe pole, gdy jest foremny.
Rozwiązanie problemu izoperymetrycznego podane jest w książce: J. Górnicki, Okruchy matematyki, WN PWN, Warszawa 2009, w artykułach Nierówności, wypukłość i ekstrema oraz Własności ekstremalne figur izoperymetrycznych.
Problematyka „ekstremalna” w przestrzeni trójwymiarowej (czyli w przestrzeni euklidesowej \(\mathbb{R}^3\)) jest odrobinę bardziej kłopotliwa. Naszym celem będzie rozwiązanie elementarnymi środkami następującego problemu:
Problem. Jaki kształt krzywej \((\)prostowalnej\()\) o długości \(L\) zapewnia, że najmniejszy zbiór wypukły zawierający tę krzywą ma największą objętość.
Krzywą nazywamy prostowalną, gdy istnieje możliwość określenia jej długości jako granicy ciągu długości łamanych coraz lepiej ją przybliżających.
Problematyka ta pojawiła się w XX wieku m.in. w pracach J. Egerváry’ego, M. Krejna, Z. Melzaka, A. Nudelmana, I. Schoenberga.
Czworościan ekstremalny.
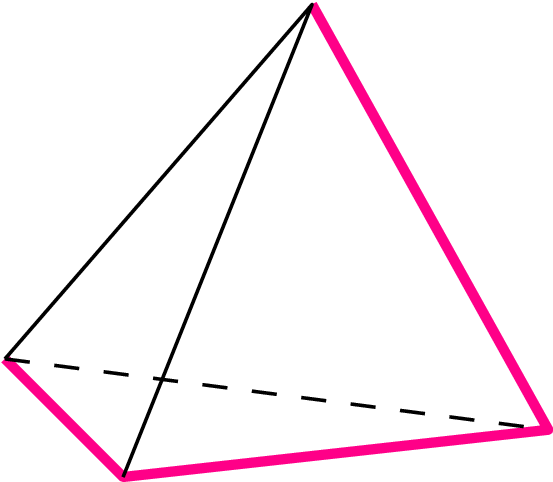
Zacznijmy od prostej sytuacji. Łamaną o czterech wierzchołkach, które nie leżą w jednej płaszczyźnie, nazywamy szkieletem czworościanu (rys. 1). Nasz problem w tym przypadku ma postać: jaki szkielet \(ABCD\) o danej długości \(AB+BC+CD=L\) rozpina czworościan \(ABCD\) o największej objętości?
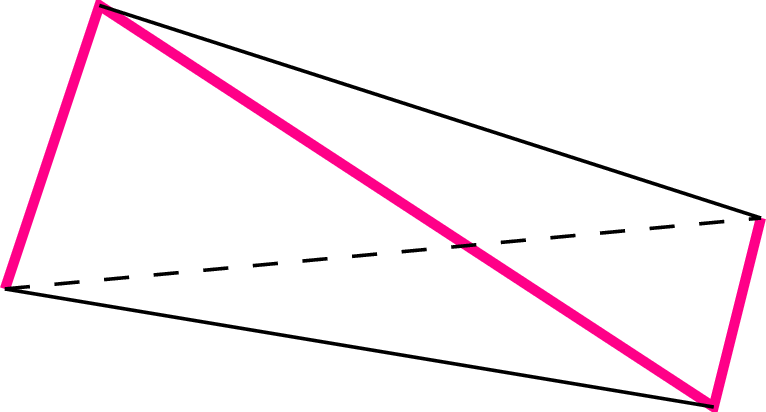
Rys. 1
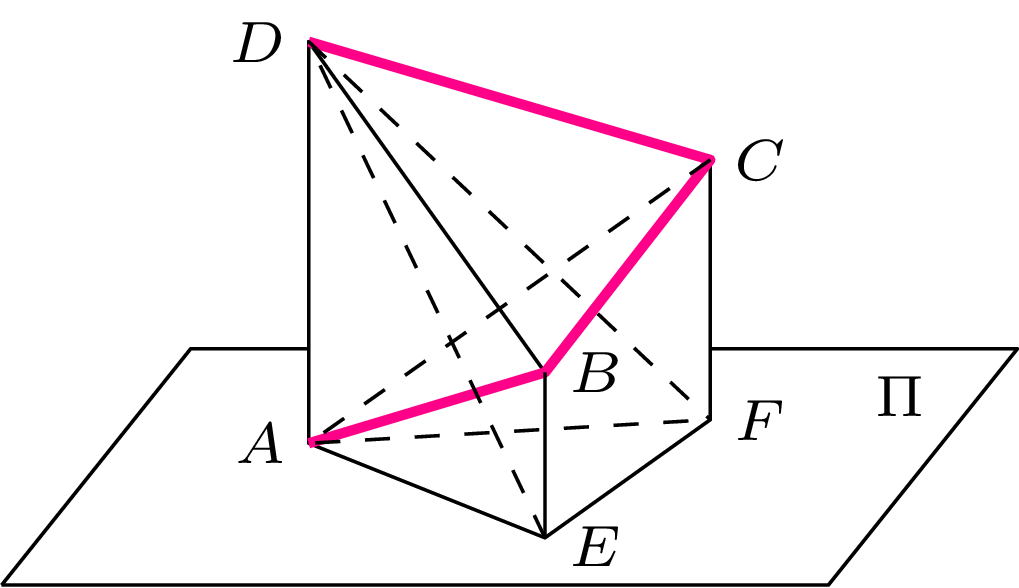
Rozwiążemy ten problem, sprowadzając go do omówionego już problemu izoperymetrycznego na płaszczyźnie. Przyjmijmy, że w czworościanie \(ABCD\) długość boku \(AD\) jest równa \(h\) (oczywiście \(h<L\)). Niech \(\Pi\) będzie płaszczyzną prostopadłą do boku \(AD\) zaczepioną w punkcie \(A.\) Wtedy rzut prostopadły czworościanu \(ABCD\) na płaszczyznę \(\Pi\) jest trójkątem \(AEF\) (rys. 2).
Rys. 2
Lemat 1. Objętość \(V\) czworościanu \(ABCD\) dana jest wzorem \[V=\frac{1}{3}hS, \tag{1}\] gdzie \(h\) jest długością boku \(AD,\) a \(S\) jest polem trójkąta \(AEF.\)
Czworościany \(ABCD\) i \(ABFD\) mają wspólną ścianę – trójkąt \(ABD.\) Ponieważ punkty \(C\) i \(F\) są w takiej samej odległości od płaszczyzny trójkąta \(ABD,\) więc objętości tych czworościanów są równe. Podobnie czworościany \(ABFD\) i \(AEFD\) mają wspólną ścianę – trójkąt \(AFD.\) Punkty \(B\) i \(E\) są w takiej samej odległości od płaszczyzny trójkąta \(AFD,\) więc objętości tych czworościanów są równe. Zatem czworościany \(ABCD\) i \(AEFD\) mają równe objętości, a objętość czworościanu \(AEFD\) wyraża się wzorem \((1).\) \(\Box\)
Lemat 2. Szkielet \(ABCD\) o długości \(L\) i odległości \(AD=h\) \((h<L)\) rozpina czworościan \(ABCD\) o największej objętości, gdy boki \(AB,\) \(BC,\) \(CD\) mają równe długości i tworzą z odcinkiem \(AD\) kąty równe \(\alpha =\arccos\frac{h}{L}.\)
Zgodnie ze wzorem \((1)\) objętość \(V\) czworościanu \(ABCD\) będzie największa, gdy największe będzie pole \(S,\) bo \(h\) jest ustalone. Musimy więc określić długość i położenie w przestrzeni boków \(AB,\) \(BC\) i \(CD\) tak, aby pole trójkąta \(AEF\) było największe. Zgodnie z twierdzeniem 1 osiągniemy to, jeśli zmaksymalizujemy obwód trójkąta \(AEF,\) jednocześnie sprawiając, że będzie to trójkąt równoboczny.
Bryła \(DABEFC\) jest wielościanem wypukłym o podstawie trójkątnej i ścianach bocznych prostopadłych do płaszczyzny \(\Pi.\)
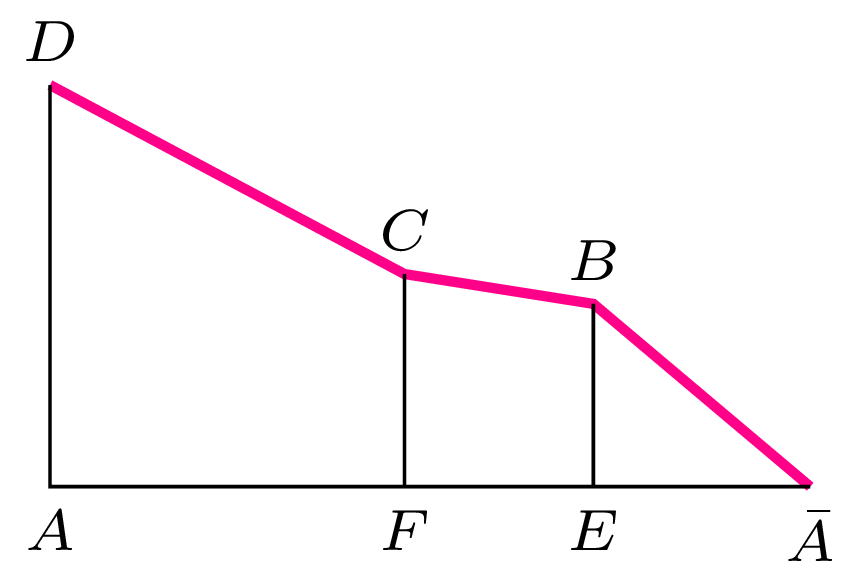
Rys. 3. Sytuacja przed optymalizacjąWielościan to bryła ograniczona płaszczyznami. Wielościan jest wypukły, gdy leży po jednej stronie każdej ze swoich ścian.
Rozetnijmy ten wielościan wzdłuż pionowych krawędzi \(DA,\) \(BE,\) \(CF\) oraz pozostałych krawędzi szkieletu. Teraz połóżmy ściany \(DAFC,\) \(CFEB,\) \(BEA\) na płaszczyźnie \(\Pi\) na zewnątrz trójkąta \(AEF.\) Następnie przesuńmy je w taki sposób, aby połączyć je pasującymi do siebie bokami (rys. 3).
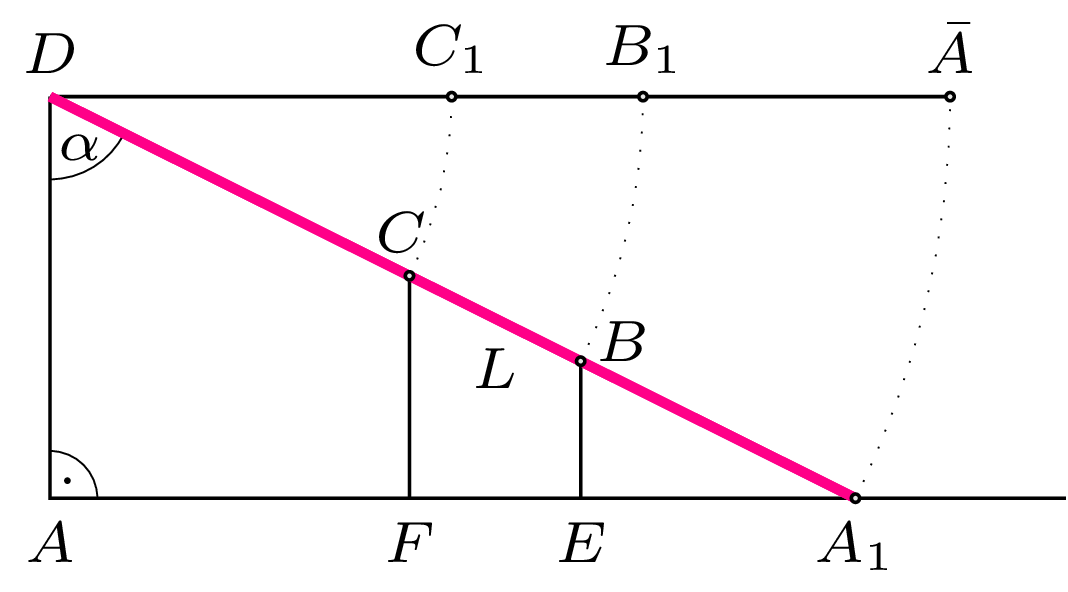
Rys. 4. Sytuacja po optymalizacji
Odcinek \(A \bar{A}\) ma długość równą obwodowi trójkąta \(AEF,\) utworzonego z rzutów prostopadłych odcinków \(DC,\) \(CB,\) \(BA\) na płaszczyznę \(\Pi.\) Rzuty te będą w sumie najdłuższe, gdy punkty \(D, C, B,\) \(\bar{A}\) (rys. 3) będą leżały na jednej prostej. Będzie ona nachylona do odcinka \(DA\) pod kątem \(\alpha =\arccos \frac{h}{L}\) (rys. 4). Warunki \(AF=FE=EA\) zapewnimy, gdy boki \(DC,\) \(CB,\) \(BA\) szkieletu \(ABCD\) będą tej samej długości. Ten opis jednoznacznie wyznacza położenie wierzchołków czworościanu: na płaszczyźnie \(\Pi\) stawiamy prawidłowy graniastosłup trójkątny, którego pionowa krawędź \(DA=h\) \((A\in \Pi),\) a podstawa ma obwód równy \(\sqrt{L^2 -h^2}.\) Kolejne odcinki \(DC,\) \(CB,\) \(BA\) leżą na kolejnych ścianach bocznych graniastosłupa, tworząc za każdym razem kąt \(\alpha = \arccos\frac{h}{L}\) z odcinkiem \(DA\) (oczywiście ten sam efekt uzyskamy, gdy kolejne odcinki \(AB,\) \(BC,\) \(CD\) będą tworzyły za każdym razem kąt \(\alpha\) z odcinkiem \(AD\)). Tak utworzony szkielet \(ABCD\) o długości \(L\) i odległości \(DA=h\) \((h<L)\) rozpina czworościan \(ABCD\) o największej objętości. \(\Box\)
Objętość tak określonego czworościanu, zgodnie ze wzorem \((1),\) jest równa \(V=\frac{\sqrt{3}}{108}\cdot h(L^2-h^2),\) gdzie \(0<h<L.\) Łatwo sprawdzamy, że przyjmuje ona wartość największą dla \(h=\frac{L}{\sqrt{3}},\) więc czworościan ekstremalny ma objętość równą \(\frac{1}{162}\cdot L^3\approx 0{,}006\cdot L^3.\) Co ciekawe, czworościan foremny o krawędzi \(\frac{L}{3}\) ma objętość równą \(\frac{\sqrt{2}}{324}\cdot L^3\approx 0{,}0044\cdot L^3,\) czyli istotnie mniejszą niż czworościan ekstremalny.
Udowodniliśmy więc następujące twierdzenie o czworościanie ekstremalnym:
Twierdzenie 3. Szkielet \(ABCD\) o długości \(L\) rozpina czworościan o największej objętości, gdy kolejne boki \(AB,\) \(BC,\) \(CD\) leżą na kolejnych ścianach bocznych prawidłowego graniastosłupa trójkątnego o pionowej krawędzi \(AD=\frac{L}{\sqrt{3}}\) i obwodzie podstawy \(\sqrt{\frac{2}{3}}\cdot L,\) a każdy z odcinków \(AB,\) \(BC,\) \(CD\) tworzy z krawędzią \(AD\) kąt \(\alpha=\arccos\frac{1}{\sqrt{3}}.\)
Wielościan ekstremalny.
Uogólnijmy teraz rozważania dotyczące czworościanu ekstremalnego na wielościany o większej liczbie wierzchołków. Łamaną \(A_0A_1A_2\ldots A_n\) \((n\geqslant 3),\) dla której każda płaszczyzna przechodząca przez punkty \(A_0\) i \(A_n\) \((A_0\neq A_n)\) ma nie więcej niż jeden punkt wspólny z łamaną \(A_1A_2\ldots A_{n-1},\) nazywamy szkieletem.
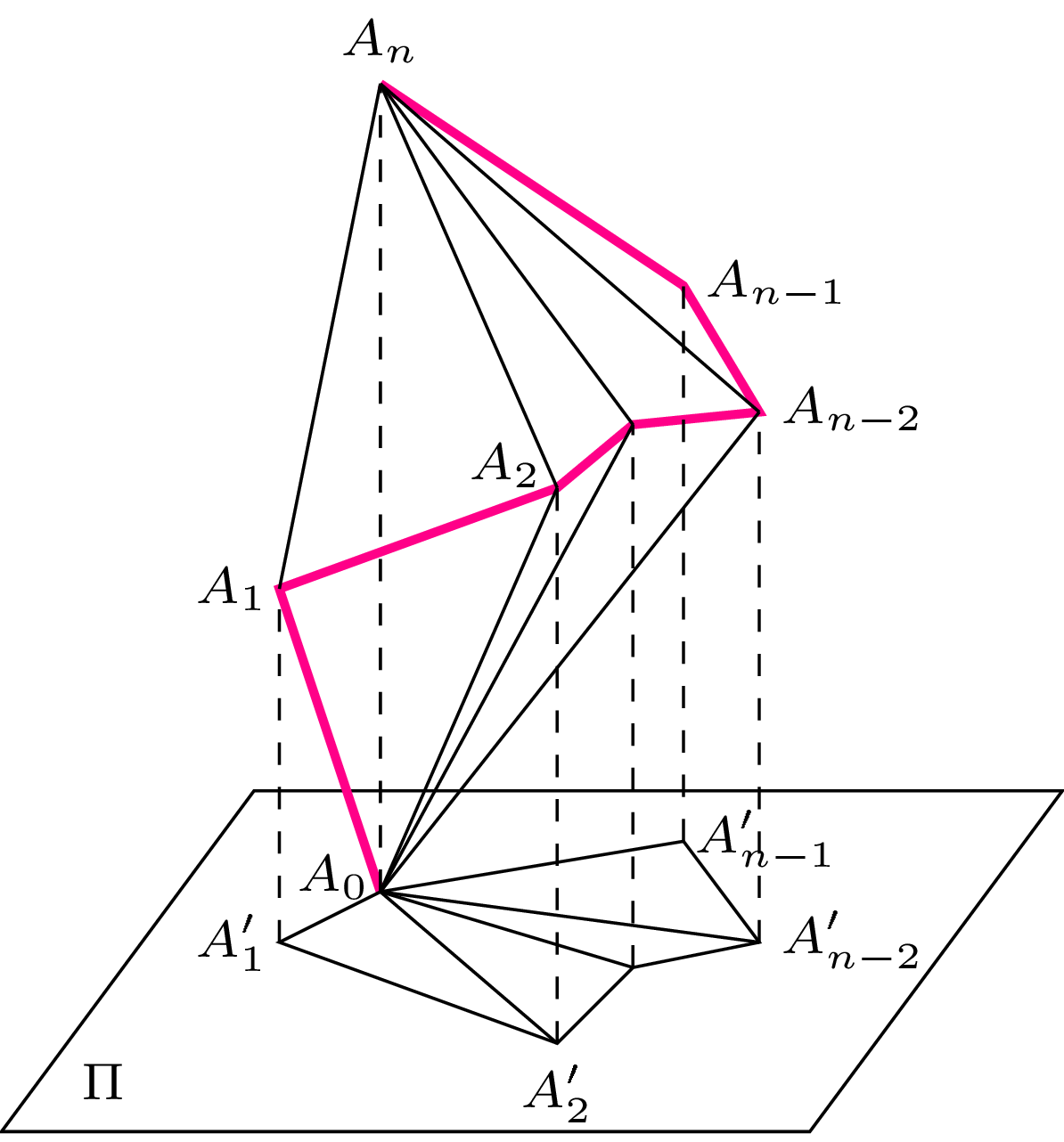
Przyjmijmy, że szkielet \(A_0A_1A_2 \ldots A_{n-1}A_n\) ma długość \(A_0A_1+A_1A_2+\ldots +A_{n-1}A_n=L,\) a długość odcinka \(A_0A_n\) jest równa \(h\) \((h<L).\) Trójkątne ściany \(A_0A_1A_n,\) \(A_0A_1A_2,\) \(A_0A_2A_3,\) \(\ldots,\) \(A_0A_{n-1}A_n\) oraz \(A_nA_{n-1}A_0,\) \(A_nA_1A_2,\) \(A_nA_2A_3,\)\(\ldots,\) \(A_nA_{n-2}A_{n-1}\) wycinają w przestrzeni \(\mathbb{R}^3\) wielościan \(A_0A_1A_2\ldots A_{n-1}A_n\) rozpięty przez szkielet \(A_0A_1A_2 \ldots A_{n-1}A_n\) (rys. 5).
Niech \(\Pi\) będzie płaszczyzną prostopadłą do odcinka \(A_0A_n\) zaczepioną w punkcie \(A_0.\) Wtedy rzut prostopadły wielościanu \(A_0A_1A_2\ldots A_{n-1}A_n\) na płaszczyznę \(\Pi\) jest \(n\)-kątem \(A_0A_1^{'}A_2^{'}\ldots A_{n-1}^{'}\) o polu \(S_n\) (rys. 5).
Rys. 5
Ponieważ wielościan \(A_0A_1A_2\ldots A_{n-1}A_n\) jest skończoną sumą czworościanów \(A_0A_1A_2A_n,\) \(A_0A_2A_3A_n,\) \(\ldots,\) \(A_0A_{n-2}A_{n-1}A_n,\) a do każdego z nich ma zastosowanie lemat 1, więc prawdziwy jest następujący rezultat:
Lemat 3. Objętość \(W_{n+1}\) wielościanu \(A_0A_1A_2 \ldots A_{n-1}A_n\) dana jest wzorem \[W_{n+1}=\frac{1}{3}hS_n, \tag{2}\]
gdzie \(h\) jest długością odcinka \(A_0A_n,\) a \(S_n\) jest polem \(n\)-kąta
\(A_0A_1^{'}A_2^{'}\ldots A_{n-1}^{'}.\)
Korzystając z twierdzenia 2 (Zenodora) oraz powtarzając rozumowanie uzasadniające lemat 2, uzyskujemy następującą konstrukcję maksymalizującą objętość wielościanu \(A_0A_1A_2\ldots A_{n-1}A_n\) rozpiętego na szkielecie \(A_0A_1A_2\ldots A_{n-1}A_n\) o długości \(L\) i odległości \(A_0A_n=h\) \((h<L)\): na płaszczyźnie \(\Pi\) stawiamy prawidłowy graniastosłup \(n\)-kątny o pionowej krawędzi \(A_0A_n=h\) \((A_0\in \Pi),\) którego podstawa ma obwód równy \(\sqrt{L^2-h^2}.\) Kolejne odcinki \(A_0A_1,\) \(A_1A_2,\) \(\ldots,\) \(A_{n-1}A_n\) leżą na kolejnych ścianach bocznych graniastosłupa, tworząc za każdym razem z odcinkiem \(A_0A_n\) kąt \(\alpha =\arccos\frac{h}{L}.\)
Ponieważ pole \(n\)-kąta foremnego \((n\geqslant 3)\) o boku długości \(a\) i kącie środkowym \(\gamma = \frac{2\pi}n\) dane jest wzorem \(S_n=\frac{1}{4}na^2\cot\frac{\gamma}{2},\) więc ze wzoru \((2)\) objętość wielościanu \(A_0A_1A_2\ldots A_{n-1}A_n\) (którego rzut prostopadły na płaszczyznę \(\Pi\) jest \(n\)-kątem foremnym) dana jest wzorem \(W_{n+1}=\frac{1}{12}\cdot h(L^2-h^2)\cdot \frac{1}{n}\cot\frac{\pi}{n}.\) Objętość ta jest największa, gdy \(h=\frac{L}{\sqrt{3}},\) i wówczas \(W_{n+1}=\frac{1}{18\sqrt{3}}L^3\cdot \frac{1}{n}\cot\frac{\pi}{n}.\) Mamy więc twierdzenie:
Twierdzenie 4. Szkielet \(A_0A_1\ldots A_n\) o długości \(L\) rozpina wielościan o największej objętości, gdy kolejne boki \(A_0A_1,\ldots ,A_{n-1}A_n\) leżą na kolejnych ścinach bocznych prawidłowego graniastosłupa \(n\)-kątnego o pionowej krawędzi \(A_0A_n=\frac{L}{\sqrt{3}}\) i obwodzie podstawy \(\sqrt{\frac{2}{3}}\cdot L,\) a każdy z odcinków \(A_0A_1,\) \(A_1A_2,\) \(\ldots,\) \(A_{n-1}A_n\) tworzy z krawędzią \(A_0A_n\) kąt \(\alpha =\arccos\frac{1}{\sqrt{3}}.\)
Rys. 6
Śrubostożek podwójny.
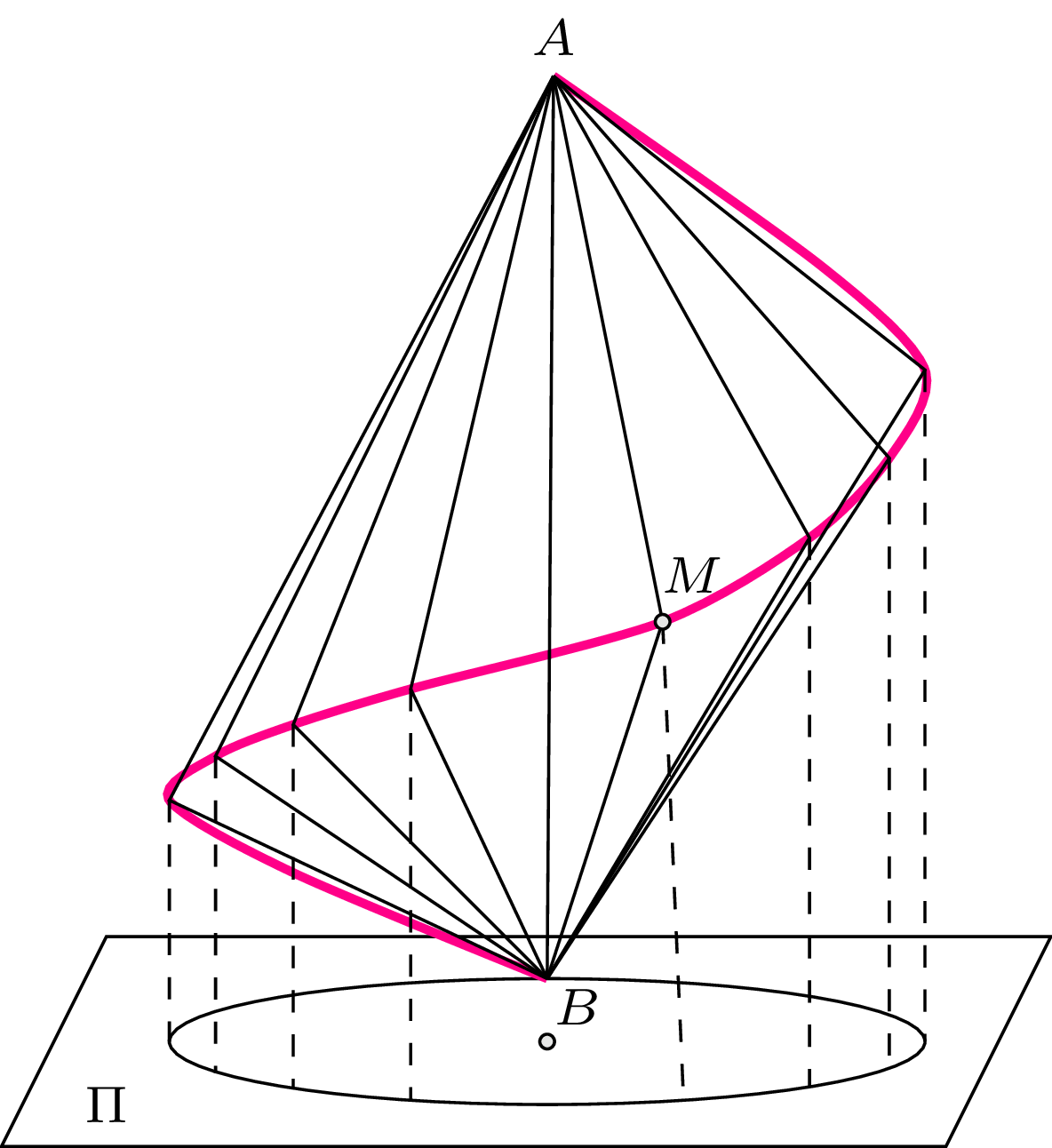
Możemy teraz przejść do rozwiązania naszego oryginalnego problemu. Z geometrii różniczkowej wiemy, że krzywa przestrzenna leżąca na powierzchni walca jest linią śrubową wtedy i tylko wtedy, gdy styczna do niej w każdym jej punkcie tworzy stały kąt z kierunkiem osi walca. Zatem gdy liczba \(n\) będzie rosła nieograniczenie, to prawidłowe graniastosłupy \(n\)-kątne coraz „ściślej” będą przylegać do walca o wysokości \(BA=\frac{L}{\sqrt{3}}\) i promieniu podstawy \(\frac{L}{\pi \sqrt{6}}\) (rys. 6), a łamana \(BA_1A_2\ldots A_{n-1}A\) (której kolejne odcinki tworzą stały kąt \(\alpha =\arccos\frac{1}{\sqrt{3}}\) z odcinkiem \(AB\) równoległym do osi walca) coraz dokładniej będzie aproksymować krzywą leżącą na powierzchni bocznej walca, która jest jednym zwojem linii śrubowej (helisy) o skoku \(\frac{L}{\sqrt{3}}.\)
Jeśli na prostokątnym arkuszu papieru narysujemy prostą, która nie jest prostopadła do któregokolwiek brzegu, i nawiniemy ten arkusz na walec o podstawie kołowej, to narysowana linia prosta przybierze kształt linii śrubowej.
Gdy środek podstawy walca o promieniu \(\frac{L}{\pi \sqrt{6}}\) jest środkiem kartezjańskiego układu współrzędnych (oś walca pokrywa się z osią \(0Z\)), to linia śrubowa o skoku \(\frac{L}{\sqrt{3}},\) leżąca na powierzchni bocznej walca dana jest równaniami parametrycznymi: \(x(t)=\frac{L}{\pi \sqrt{6}}\cdot \cos t,\) \(y(t)=\frac{L}{\pi \sqrt{6}}\cdot \sin t,\) \(z(t)=\frac{L}{2\pi\sqrt{3}}\cdot t,\) gdzie \(0\leqslant t\leqslant 2\pi\) oraz \(B=(x(0),y(0),z(0)),\) \(A=(x(2\pi),y(2\pi),z(2\pi))\) (rys. 6).
Jeśli punkt \(M\) porusza się po linii śrubowej, to odcinki \(BM\) oraz \(AM\) zakreślają powierzchnie stożkowe i powstaje bryła śrubostożek podwójny (rys. 6). Ponieważ \(\lim\limits_{n\rightarrow\infty}\frac{1}{n}\cot\frac{\pi}{n}=\frac{1}{\pi},\) więc objętość tak powstałego śrubostożka podwójnego jest równa \(\lim\limits_{n\rightarrow\infty}W_{n+1}=\frac{1}{18\pi\sqrt{3}}L^3\approx 0{,}01\cdot L^3.\)
Ostatecznie otrzymujemy rozwiązanie postawionego problemu:
Twierdzenie 5 (J. Egerváry, 1949). Spośród wszystkich brył rozpiętych na gładkiej krzywej o długości \(L\) największą objętość ma bryła będąca otoczką wypukłą jednego zwoju linii śrubowej o skoku \(\frac{L}{\sqrt{3}}\) na powierzchni walca kołowego o promieniu podstawy \(\frac{L}{\pi \sqrt{6}}.\)