Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Polecam następującą zagadkę: skonstruować trzy pętle („pierścienie”) \(A,\) \(B,\) \(C\) w taki sposób, by:
tworzyły one nietrywialny splot, a więc np. by pętli \(C\) nie dało się wyjąć na zewnątrz;
każda para tworzyła trywialny splot, czyli np. po usunięciu \(C\) pozostałe pętle \(A,\) \(B\) dało się rozdzielić.
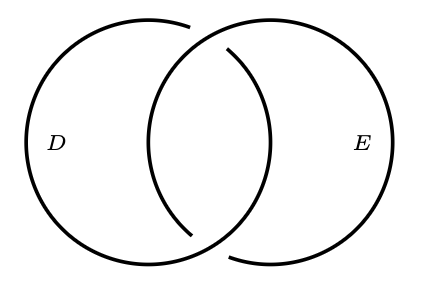
Dla ilustracji podaję obok przykład nietrywialnego splotu dwóch pętli (rys. 1). Nietrywialność można rozpoznać po tym, że idąc wzdłuż \(D,\) raz przechodzimy nad \(E,\) a raz pod. Rozwiązanie tej zagadki poniżej, tymczasem wskazówka: zacząć od umieszczenia pętli \(A\) i \(B\) jak na rysunku 2 (mogą nawet na siebie nachodzić, byle nie były splątane), po czym poprowadzić pętlę \(C\) w taki sposób, by kolejne „przecięcia” z pętlą \(A\) się znosiły, czyli np. układały w ciąg nad-nad-pod-pod lub nad-pod-pod-nad; podobnie z pętlą \(B\) – w ten sposób unikniemy splotu par \(A,C\) i \(B,C.\) Pozostaje przeprowadzić to w taki sposób, by cała trójka była splątana.
Rys. 1. Przykład nietrywialnego splotu pętli \(D\) i \(E\) (splot Hopfa)
Najprostsze rozwiązanie głównej zagadki to pierścienie Boromeuszy, poniżej w wersji klasycznej oraz trójkątnej (valknut).


Źródło: Wikimedia Commons
Najprostsze rozwiązanie tej zagadki bierze swoją nazwę od włoskiego rodu Boromeuszy, który umieścił je w swoim herbie. Według niektórych źródeł splot ten symbolizował więzy łączące trzy rodziny arystokratyczne – Boromeuszy, Sforzów i Viscontich – a według innych odnosił się do Trójcy Świętej. Był też chętnie stosowany wcześniej przez ludy germańskie (w swojej trójkątnej formie znanej jako valknut), jak i poza Europą. Jaki jednak ma to związek z wieszaniem obrazków rozważanym przez Marię Pieczarkę w obecnym numerze?
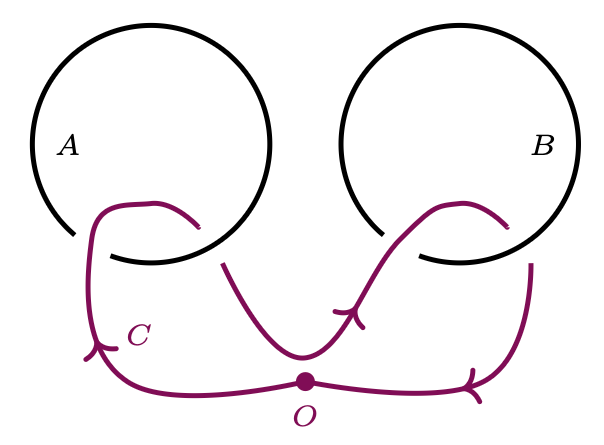
Otóż jest to po prostu ta sama zagadka! W zobaczeniu tego pomoże opis formalny, nieco odmienny od języka przejść nad i pod. Ustalmy jakiś punkt zaczepienia \(O\) i prowadźmy pętlę \(C\) etapami: w jednym kroku wychodzimy z \(O,\) przechodzimy przez jedną z pętli \(A\) lub \(B\) i wracamy do \(O.\) Zanotujmy przy tym kolejne kroki: niech \(a\) odpowiada przejściu przez \(A\) z góry na dół, \(a^{-1}\) podobnie, tylko z dołu do góry, a \(b\) oraz \(b^{-1}\) analogicznie dla \(B.\) Przeanalizujmy następnie otrzymany napis. Dla przykładu: \(ab\) odpowiada zwyczajnemu łańcuchowi złożonemu z trzech ogniw (rys. 2), który spełnia prawie wszystkie warunki zagadki – niestety usunięcie \(A\) pozostawia \(B\) i \(C\) nadal splątane. Odnotujmy, że przyporządkowanie napisowi odpowiadającej mu pętli jest wzajemnie jednoznaczne, jeśli umówimy się, że napisy można „skracać”, np. utożsamiając \(aaa^{-1}b\) z \(ab\) (polecam zastanowić się, dlaczego to są dwa sposoby opisu tej samej pętli), przy czym zamiana kolejności symboli jest niedozwolona. Ta obserwacja nie jest łatwa w dowodzie, ale chyba odpowiada intuicji.
Rys. 2. Trywialny splot \(A\) i \(B\) jako zaczątek rozwiązania zagadki. Kolorem zaznaczona jest pętla \(C\) odpowiadająca przykładowemu napisowi \(ab\)
Po przeczytaniu artykułu o wieszaniu obrazka nie powinno dziwić, że właściwym rozwiązaniem okazuje się… pętla \(C\) opisana poprzez \(a b a^{-1} b^{-1}.\) Rzeczywiście, usunięcie pętli \(B\) powoduje, że symbole \(b\) i \(b^{-1}\) można pominąć, pozostawiając \(aa^{-1},\) a to skraca się do pustego napisu, czyli pętli trywialnej (niepołączonej z \(A\)); podobnie jest przy usunięciu \(A.\) Warto pamiętać, że nie jest to jedyne rozwiązanie. W artykule Jacka Gładysza z \(\Delta^{1}_{18}\) pojawia się inny naturalny splot, spopularyzowany przez Martina Gardnera, i okazuje się, że istotnie różni się on od splotu Boromeuszy. Jakiemu napisowi odpowiada? Pozostawiam Czytelnika z tym pytaniem.
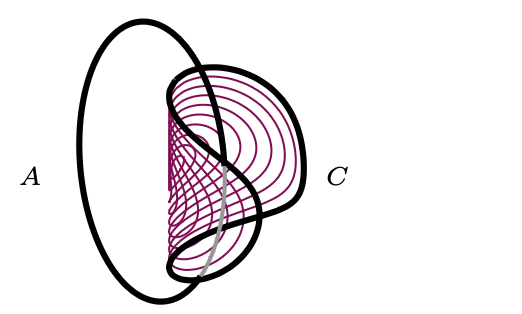
Proponuję jeszcze trzy zagadki związane ze splotem Boromeuszy. W ramach wstępu do pierwszej z nich zauważmy, że na pętli \(C\) nie da się rozpiąć dysku, który byłby rozłączny z \(A\) i \(B\) – inaczej \(C\) dałoby się ściągnąć do punktu bez zahaczenia o pozostałe pętle (rys. 3). Ale da się rozpiąć co innego:
Rys. 3. Na pętli \(C\) rozpięto „dysk” rozłączny z \(A.\) Umożliwia to stopniową deformację pętli \(C\) poprzez ściąganie jej do punktu, co zaznaczono kolorowymi liniami
Zagadka 2. W splocie Boromeuszy znaleźć powierzchnię rozpiętą na pętli \(C,\) czyli mającą \(C\) jako swój brzeg, a jednocześnie rozłączną z pętlami \(A\) i \(B.\)
(Zarys) Pętle \(A\) i \(C\) nie są splecione, więc nasz splot możemy przekształcić do poniższego (od lewej: \(A,B,C\)). Teraz na \(C\) rozpinamy płaski dysk – jest on rozłączny z \(A,\) ale przecina \(B\) w dwóch miejscach. By usunąć przecięcia, wycinamy w dysku dwa okrągłe otwory. Wreszcie otwory te zalepiamy, wklejając „rurkę” od jednego do drugiego z nich. To już można zrobić bez kolizji, prowadząc tę rurkę wzdłuż pętli \(B\) niczym oplot kabla.
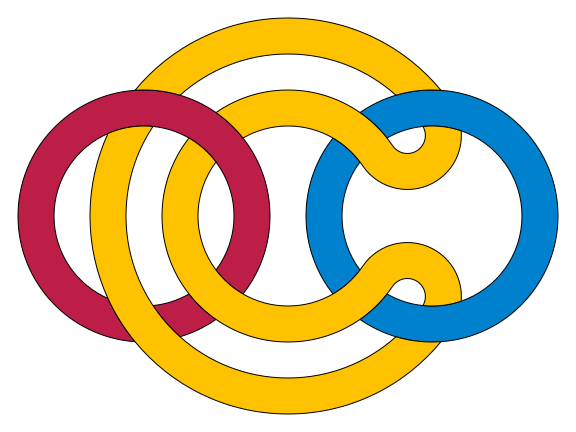
Źródło: Wikimedia Commons
Warto zwrócić uwagę, że na rysunku 1 podobne zadanie byłoby niemożliwe – na pętli \(D\) nie da się rozpiąć żadnej powierzchni rozłącznej z \(E.\) Okazuje się tu kluczowe, że napis \(aba^{-1}b^{-1}\) skraca się, jeśli dopuścimy zamianę symboli miejscami (bo \(aa^{-1}bb^{-1}\) sprowadza się do pustego napisu). Pełne wyjaśnienie tego fenomenu można odnaleźć w twierdzeniu Hurewicza, na którego omówienie niestety brakuje tu miejsca.
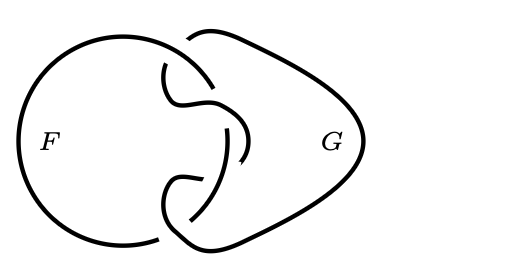
Zagadka 3. Znaleźć powierzchnię rozpiętą na \(F\) i rozłączną z \(G\) (rys. 4). Czy jest ona dwustronna czy jednostronna? (inaczej: orientowalna czy nie?)
Powierzchnię tę konstruujemy jak w zagadce 2: na \(F\) rozpinamy dysk, wycinamy dwa otwory i wklejamy rurkę. Jedyna różnica jest taka, że teraz jeden koniec rurki jest doprowadzony „od góry”, a drugi „od dołu”, więc zewnętrzna powierzchnia rurki łączy górną i dolną część dysku. W efekcie otrzymujemy powierzchnię jednostronną, a więc nieorientowalną. Istnienie takiej powierzchni może zaskakiwać, ale również jest wyjaśniane przez twierdzenie Hurewicza, tym razem ze współczynnikami w \(\mathbb{Z}_2.\)
Rys. 4. Pętla \(G\) jest dwukrotnie nawinięta na okrąg \(F,\) a mimo to na \(F\) da się rozpiąć powierzchnię rozłączną z \(G\)
Zagadka 4. Znaleźć powierzchnię rozpiętą na splocie Boromeuszy, czyli taką, której brzeg składa się z trzech okręgów \(A,\) \(B,\) \(C.\)
Przykładowe rozwiązanie widać niżej. Powierzchnię tego typu (zwartą, spójną, zorientowaną, o z góry zadanym brzegu) nazywamy powierzchnią Seiferta. Można podać prosty przepis (algorytm Seiferta) na taką powierzchnię w ogólnym przypadku, ale nie zmieściłby się na tym marginesie.

Źródło: Accelerometer, Wikimedia Commons, CC BY-SA 3.0
Podobnie dla każdego innego splotu (lub węzła) da się znaleźć rozpiętą nań powierzchnię orientowalną (nawet więcej niż jedną), nazywaną powierzchnią Seiferta – pożytki z istnienia takiej powierzchni to również temat na inną opowieść.